0 引言

在中国提出“双碳”目标之后，高比例可再生能源接入与高比例电力电子设备应用的“双高”电力系统已经逐渐成为中国电网发展的主要趋势[1]。能量路由器（energy router，ER）可以变换电压等级，控制能量分布，保证配电网运行的经济性、稳定性以及安全可靠性[2-4]，是柔性交直流配电网的核心设备之一。电磁暂态仿真是研究ER电气特性的一种主要方式。根据ER的工作原理可以得到传统的电磁暂态详细模型（detail model，DM），这种仿真模型具有大量的功率模块和开关器件，拓扑结构较为复杂，在高开关频率的仿真场景下，该模型的仿真速度往往无法满足工程实际的需求[5-7]。

为了解决高开关频率对仿真步长的限制，文献[8-9]推导出单台双有源桥（dual active bridge，DAB）的平均值模型，从详细模型下的暂态分量出发，对详细模型进行简化处理，得到等值阻抗与其他相关参数，最后比较了2种模型下的仿真波形。文献[10]深入研究了带有LLC谐振器的双有源桥，用阻感支路加受控源的形式来表示变压器，同时对开关设备进行了等值处理，简化了该模型的拓扑结构。文献[11]针对多有源桥（multi-active bridge，MAB）建立了上述等值模型，基于该模型实现对整个电网的仿真计算。除以上理论建立的模型外，文献[12]基于傅里叶变换建立了一种双有源桥的动态相量模型，同样能够增大仿真步长，进而提高仿真效率。当仿真计及高次谐波时，这种动态相量模型可以显著提高仿真精度。然而在通常的仿真场景中，为了符合工程实际的需求，往往忽略高次谐波的作用，导致仿真精度无法达到以上效果。与平均值模型相同，动态相量模型的建立也是基于换流器的外特性，而忽略了内部的拓扑结构及电气特性，以此来增大仿真步长。平均值模型和动态向量模型都只能表征设备的部分特性，且由于对换流器进行了简化处理，使模型中出现不可忽略的截断误差，仿真结果的精确度也因此有所降低。

当仿真对象具有复杂拓扑，即包含大量子模块与转换设备时，为了对节点导纳矩阵进行降阶处理，进而简化计算。通常是从设备的外特性出发，经过一系列等值化简，得到具有简单拓扑的仿真模型，最后接入外部系统。文献[13]基于模块化多电平换流器的拓扑结构提出一种戴维南等值模型，通过各个子模块的等值与叠加推导出仅含设备外部节点的等值模型，减小了求解方程的维数，进而提高了仿真效率。除此之外，文献[14-17]依据二端口网络的特性，提出一种嵌套快速求解法，同样地减少了网络的节点数量，得到维数远小于节点导纳方程的端口网络方程。然而这种求解法在计算之前需要进行预处理，对于拓扑结构不断更新的系统，尤其是具有多端口结构的网络，端口网络方程的推导难度显著增大。此外，电磁暂态仿真历史量的更新需要对相关的电气量进行反解计算，而在上述方法中，这些电气量是通过外部信息计算得到的，在设备内部的网络结构过于复杂时，仿真效率往往无法满足要求。

电磁暂态仿真根据仿真速度的不同有离线仿真与实时仿真2种形式。离线仿真可以在Matlab/Simulink或PSCAD/EMTDC等软件中实现，但其依赖于硬件资源的条件，仿真速度并不理想。为了使仿真效率满足需求，文献[18-19]在RT-LAB平台上建立了纳秒级时间尺度的实时仿真模型。文献[18]针对输入串联输出并联（input series output parallel，ISOP）型双有源桥，建立恒导纳模型，将开关器件以受控源的形式等值替换。然而这种等值形式在模型中引入了数值较小的电容与电感，导致模型中出现虚拟功率。同时，恒导纳模型的参数取决于外部条件，增加了建模难度。文献[19]将变压器的等值电感差分化，进而把DAB单元的计算分解开来，分别由2个电气硬件仿真解算器（electrical hardware simulation，EHS）模块负责。但由于在离散化过程中使用了前向欧拉法，无法避免非状态变量引发的数值振荡问题。

文献[20]提出半隐式延迟解耦电磁暂态仿真方法（semi-implicit latency decoupling and paralleling technology，SILDP），本文将这种方法用于拓扑较为复杂的多端口ER高效电磁暂态仿真，提出一种通用的ER解耦与并行计算方法，能够适应不同类型的拓扑。本文基于半隐式延迟解耦电磁暂态仿真方法，首先形成单个全桥子模块的状态方程，应用矩阵分裂和延迟技术建立全桥子模块的半隐式解耦模型。而后基于二端口网络原理得到多个子模块级联和并联形式的等值模型，并建立功率耦合拓扑解耦模型。再把以上所建立的模型组合在一起，得到能量路由器的半隐式解耦模型。最后通过搭建详细模型和本文的半隐式延迟解耦模型并进行比对，验证了方法的准确性和有效性。

1 能量路由器拓扑

能量路由器拓扑主要有以下4种类型[21-24]。

1）串型拓扑。如图1所示，是最典型的ER拓扑。能够实现功率在端口间的串行流动，但端口之间故障不能独立。

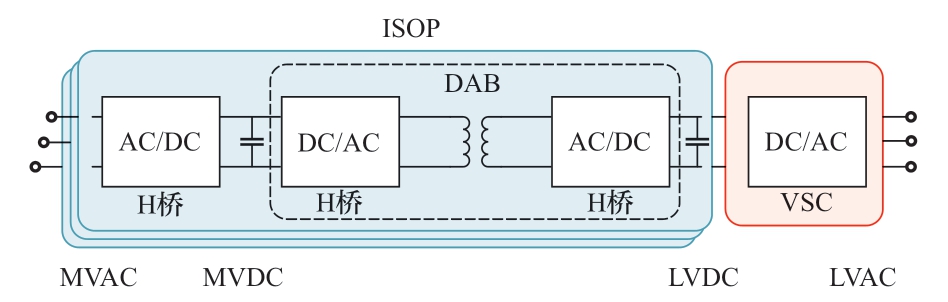
图1 传统串型多端口拓扑
Fig.1 Traditional serial multi-port topology

2）共直流母线拓扑。如图2所示，功率可在端口之间传输，故障可独立，但电能变换环节冗余。

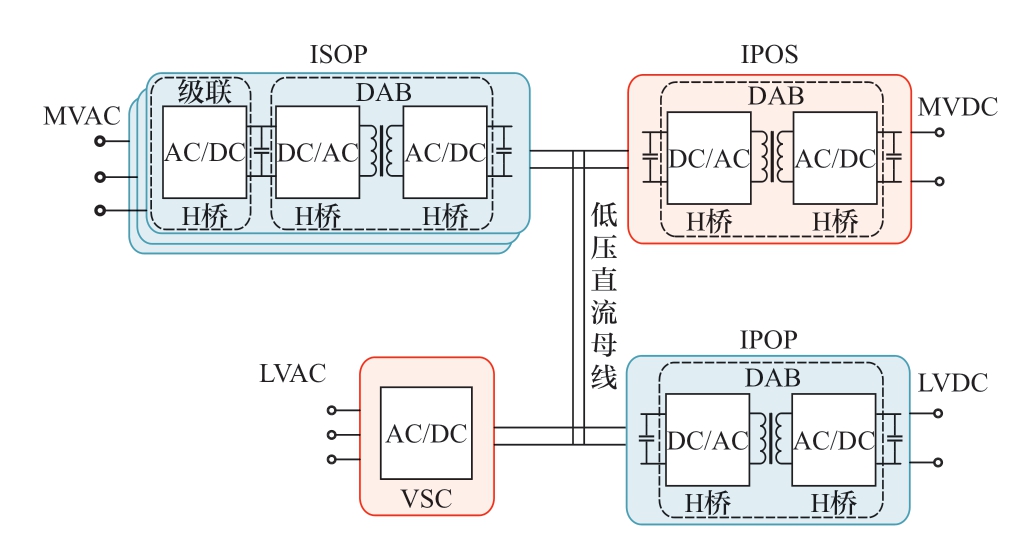
图2 共直流母线多端口拓扑
Fig.2 Common DC bus multi-port topology

3）基于MAB的多端口拓扑。如图3所示，2018年投运的张北柔性变电站采用的是这种拓扑结构。该拓扑对共直流母线拓扑中冗余的电能变换部分进行精简，用多绕组高频变压器实现各端口的功率耦合，但是多绕组变压器需特别设计，制造困难。

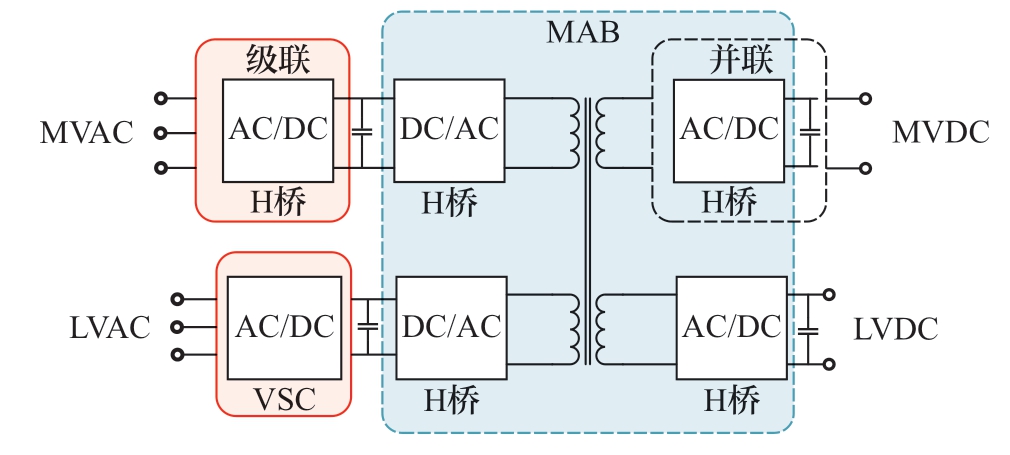
图3 基于MAB的多端口拓扑
Fig.3 MAB-based multi-port topology

4）星型共高频链多端口拓扑，也称共交流母线拓扑。如图4所示，通过把多绕组高频变压器换成每个端口的双绕组高频变压器，用多组互联的方式完成多绕组的效能，拓展性更好，设计难度降低。

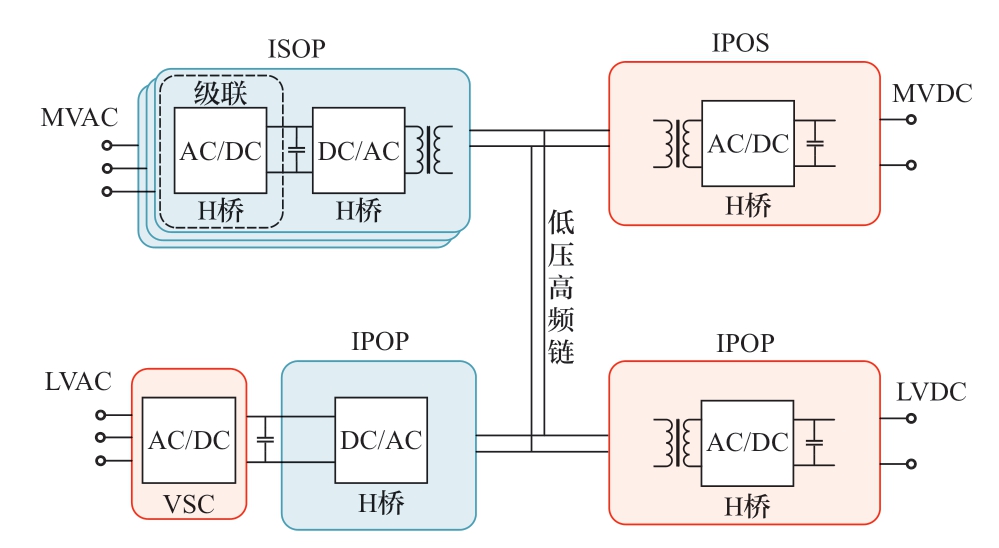
图4 星型共高频链多端口拓扑
Fig.4 Star-shaped common high-frequency chain multi-port topology

上述4种拓扑中，ER均可看作由2部分构成，即各端口的电能变换部分和高频链功率耦合部分。其中，高频链功率耦合部分又包含通常由H桥构成的AC/DC和DC/AC变换环节，双绕组或多绕组变压器构成的功率耦合环节。

2 能量路由器的解耦

文献[20]提出了半隐式延迟解耦法，下面将该方法应用于能量路由器的解耦。

2.1 H桥解耦模型

图5 （a） 为H桥的详细模型。iL为端口电感电流，vL为端口电压，vC为H桥直流侧电容电压，iC为流入的直流侧电流。将IGBT与其反并联的二极管看成一个开关对，计及导通损耗的开关函数模型拓扑如图5 （b）所示，其中Ron=0.01 Ω。

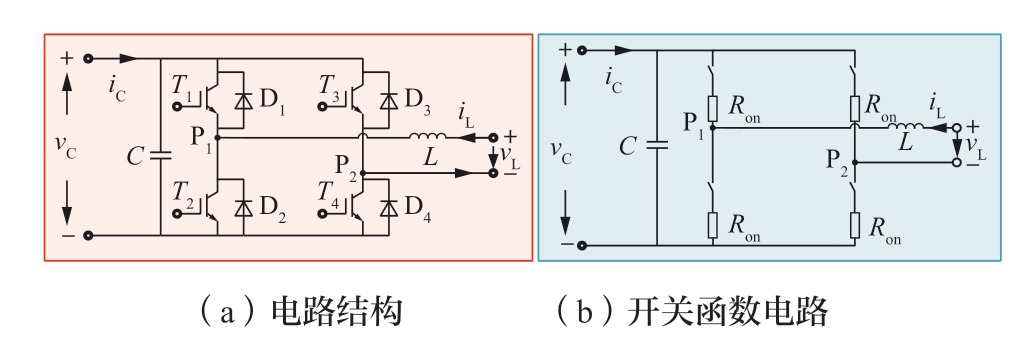
图5 H桥电路
Fig.5 H bridge circuit

定义开关函数

式中：S1表示第1个与第2个开关对对应桥臂的开关函数；S2表示第3个与第4个开关对对应桥臂的开关函数。

以iL和vC为状态变量，依据替代定理可以建立H桥的状态方程：

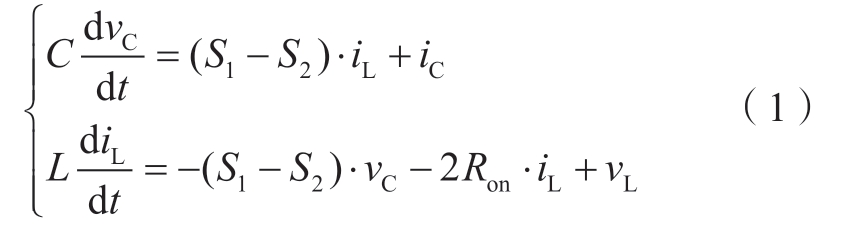
写成状态空间方程形式如下。

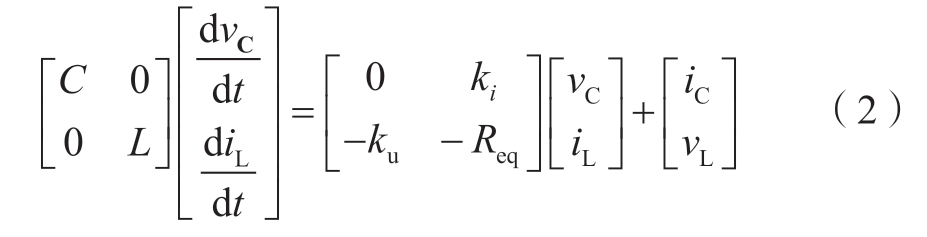
式中：Req=2Ron，ku = ki = S1 - S2。

对状态方程应用矩阵分裂技术，将状态变量分为iL和vC两个部分，使式（2）转换成如下形式：

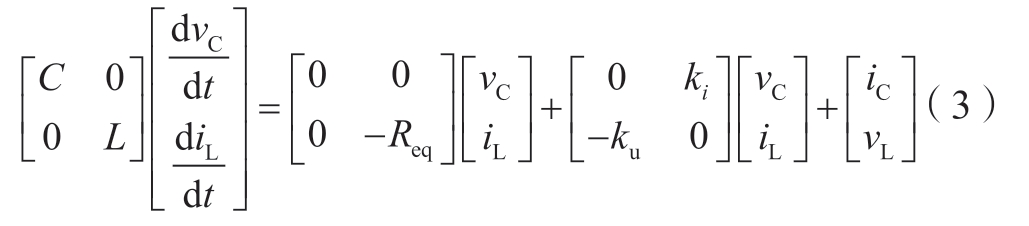
从状态方程的分裂形式出发，应用延迟技术，引入半个时间步长的延迟，得到解耦后的方程。

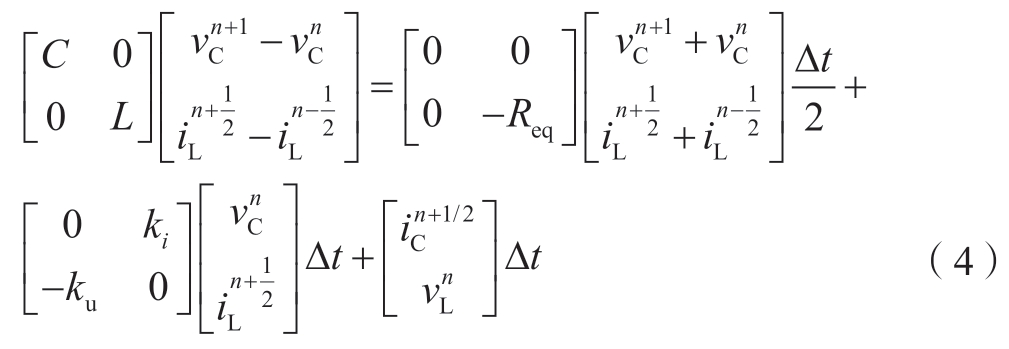
展开可得迭代式

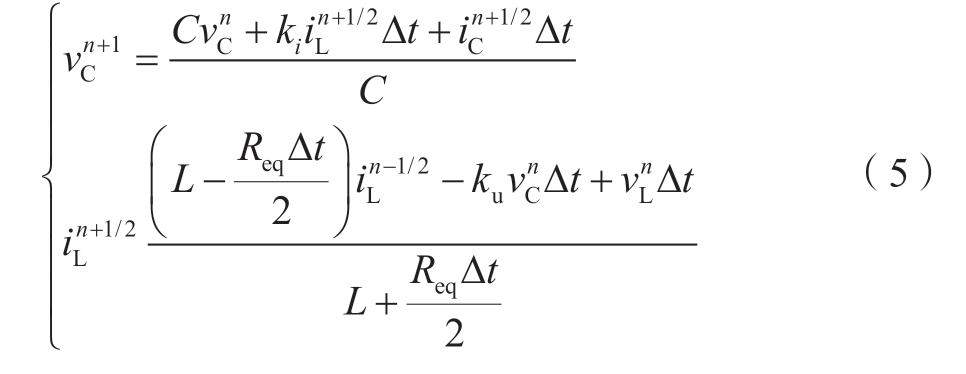
与式（3）和（4）对应的解耦电路如图6所示。图中 Jeq=kiiL，Veq=kuvC。

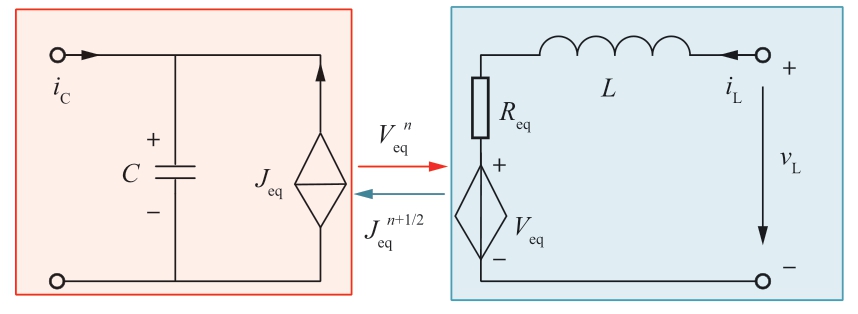
图6 H桥电路等效解耦图
Fig.6 Equivalent decoupling graph of H bridge

2.2 端口电能变换拓扑解耦

能量路由器的端口形式一般包括中压交流端口、中压直流端口、低压交流端口、低压直流端口。各端口的拓扑根据电压和功率的大小通常为如下形式。

2.2.1 H桥级联

MVAC、MVDC端口为了提高电压等级，通常采用多个H桥串联形成H桥级联端口。根据2.1节中推导的H桥解耦电路，可以很容易的得到级联H桥的等值电路，如图7所示。

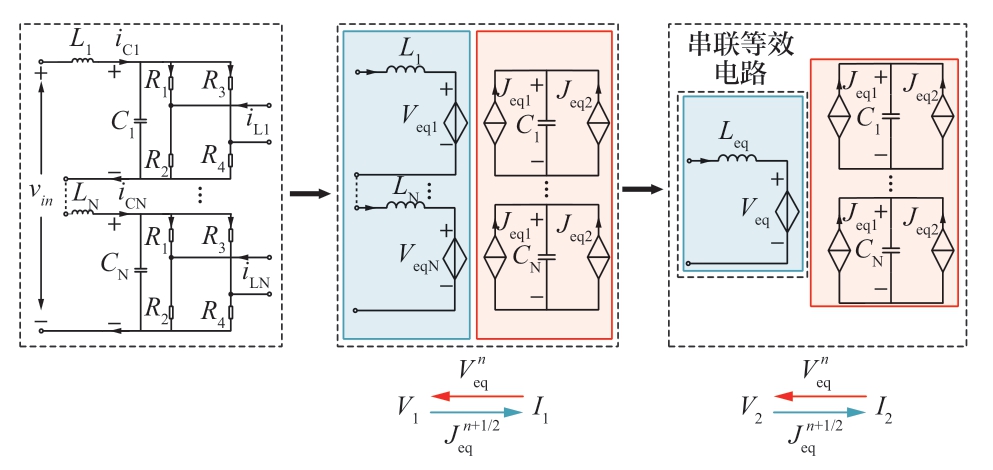
图7 级联H桥解耦模型
Fig.7 Decoupling model of cascaded H bridge

其中级联部分的参数为：

2.2.2 H桥并联

当设备需要输出更多功率时，可以令若干个H桥输出端并联（如LVDC、MVDC端口）。与级联H桥同理，并联H桥的解耦模型如图8所示。

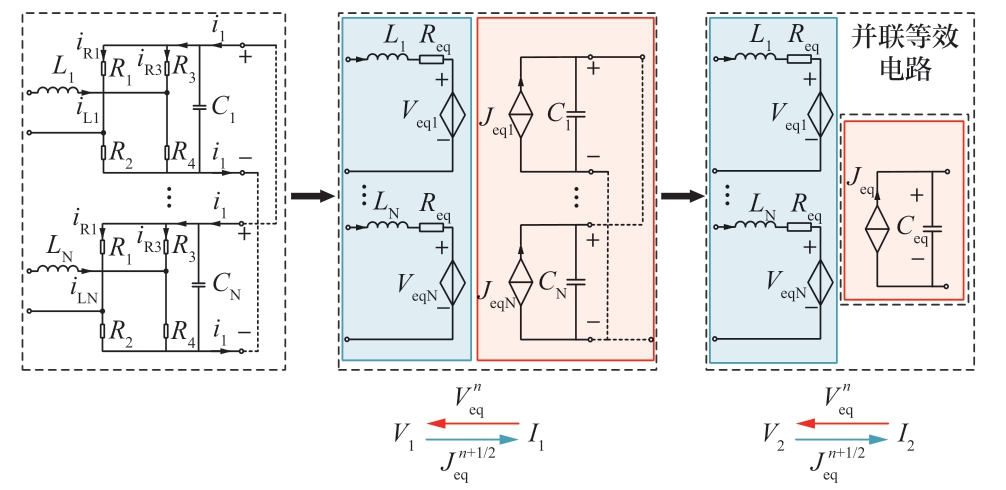
图8 并联H桥解耦模型
Fig.8 Decoupling model of parallel H bridge

其中并联部分的参数为：

2.2.3 VSC逆变器解耦

LVAC端口通常采用VSC逆变器，对其也可以采用半隐式延迟解耦方法进行交直流侧的解耦。本文主要研究ER的解耦，VSC的解耦不作过多介绍。

2.3 功率耦合拓扑的解耦

如图1—3所示，ER的功率耦合环节包括2个组成部分，即全桥子模块与变压器。根据拼接形式和绕组数量的不同组合，功率耦合环节也有多种形式，最为常见的结构就是第1章所示的双有源桥与多有源桥。对于单个能量路由器子模块来说，与高频变压器相关的节点数量并不算多，因此可以跳过变压器的解耦环节，将解耦后的换流器模块直接与变压器组合，得到功率耦合环节的解耦模型。省去高频变压器的解耦后，便将功率耦合环节的解耦置于一个通用的框架下，此时原本的电路无论采用怎样的结构，解耦模型的形式都是一致的，因此很容易进行推广，也降低了程序设计的复杂程度。

下面分析拓扑结构相对复杂的多有源桥的解耦电路，图9为其中常见的2类高频变压器。

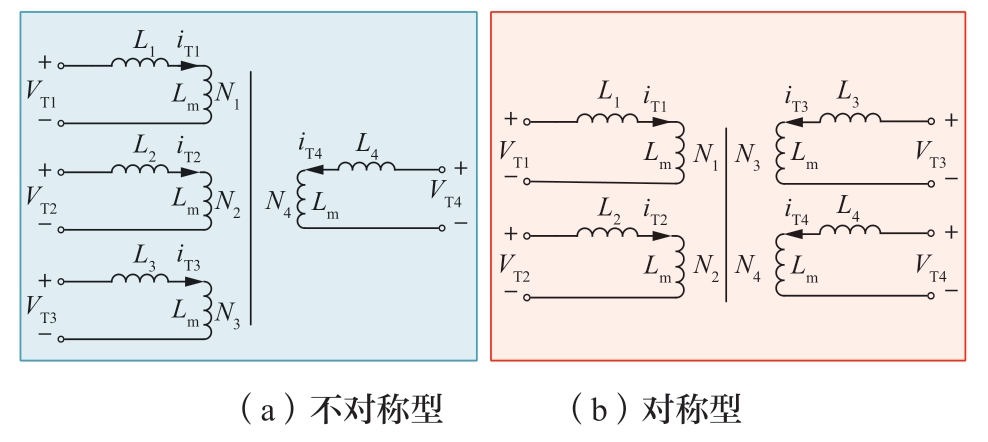
图9 MAB拓扑
Fig.9 MAB topology

根据基尔霍夫电压定律，将绕组上的电感电流作为独立状态变量列写状态方程：

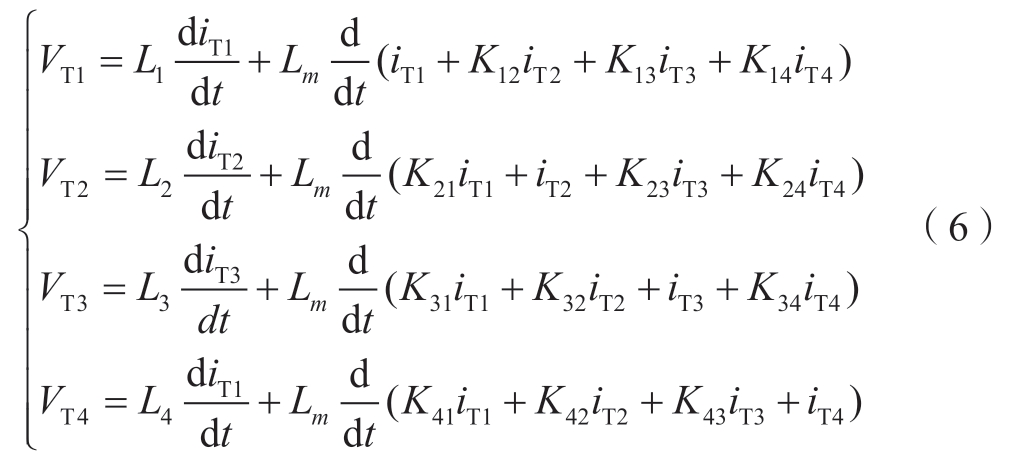
式中：N表示绕组匝数，K表示绕组间的变比。

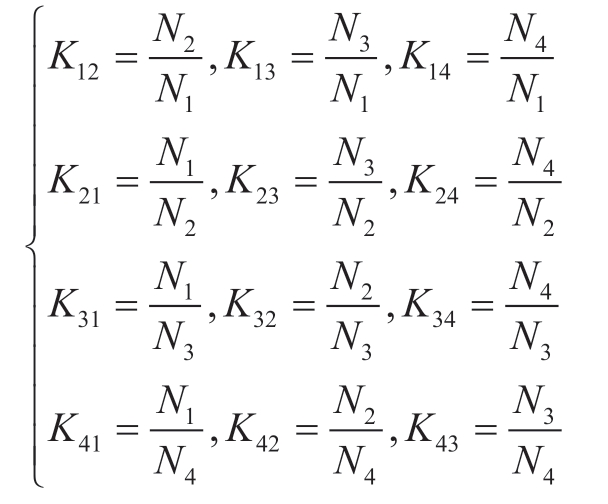
根据图3所示，变压器电感电流iTk(k=1,2,3,4)等于对应的各个全桥子模块的端口电流，将式（6）与式（2）联立，推导出MAB的状态空间方程，方程结构同式（2）。因此根据H桥的解耦方式，可以推导出MAB模块的解耦模型，等值电路见图10。观察等值电路发现，MAB的解耦电路实际上是变压器模块与H桥解耦子模块直接连接形成的，对于任何一种拓扑都表现为这样的结构。

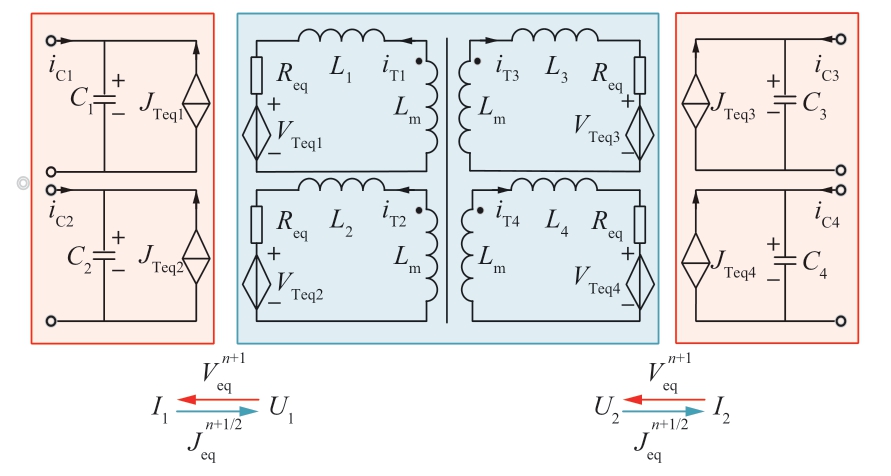
图10 四绕组变压器简化等效电路
Fig.10 Simplified equivalent circuit of four-winding transformer

2.4 能量路由器拓扑解耦模型

类似地，把功率耦合环节与各个解耦子模块用同样的方式组合起来，形成不同拓扑的ER整体解耦电路，如图11—14所示。

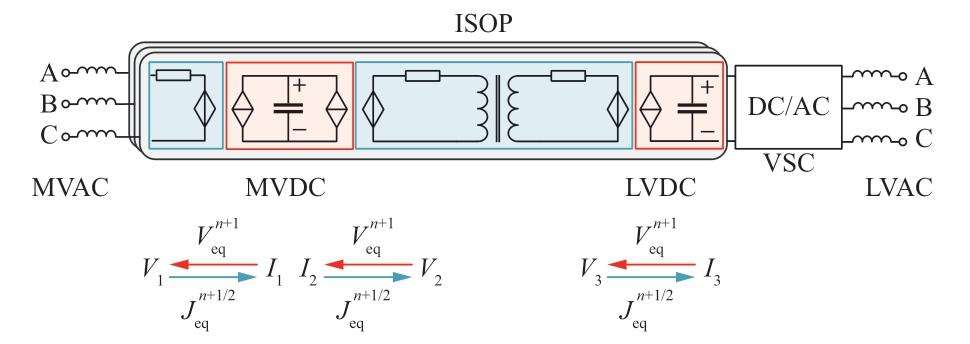
图11 传统串型多端口拓扑解耦电路图
Fig.11 Decoupling circuit diagram of traditional serial multi-port topology

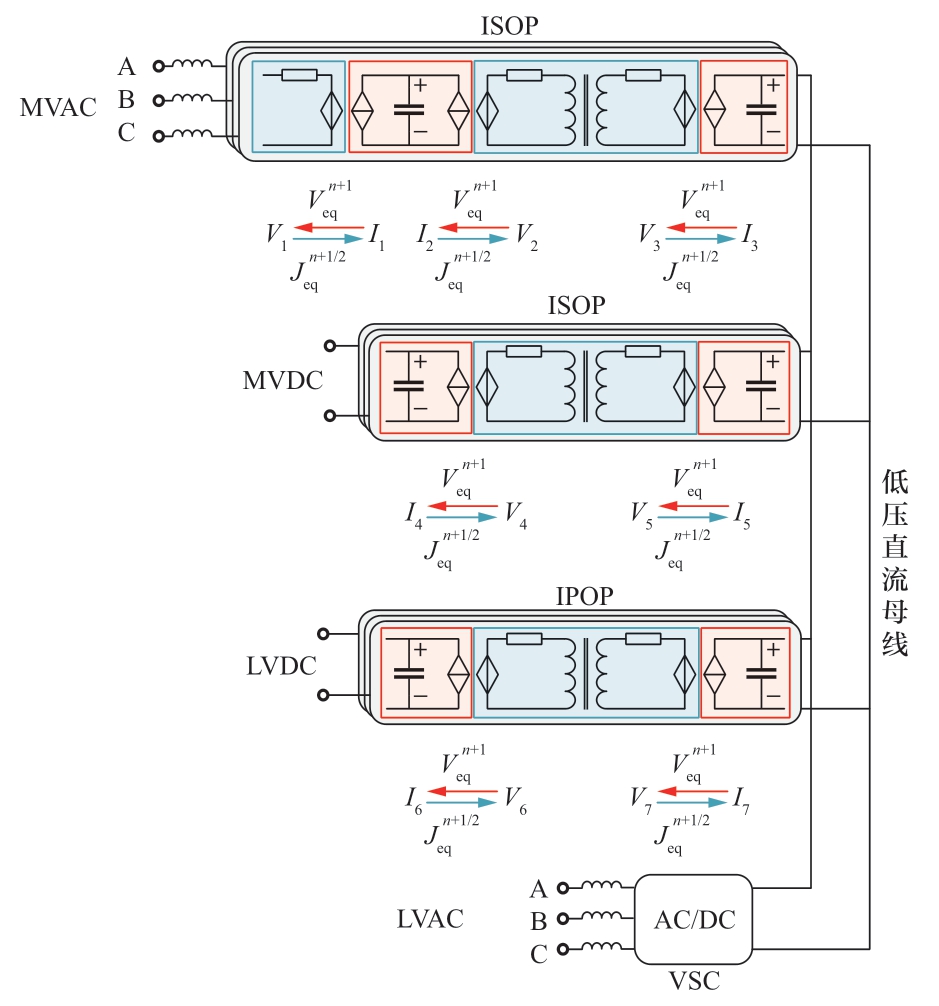
图12 共直流母线多端口拓扑解耦电路图
Fig.12 Decoupling circuit diagram of common DC bus multi-port topology

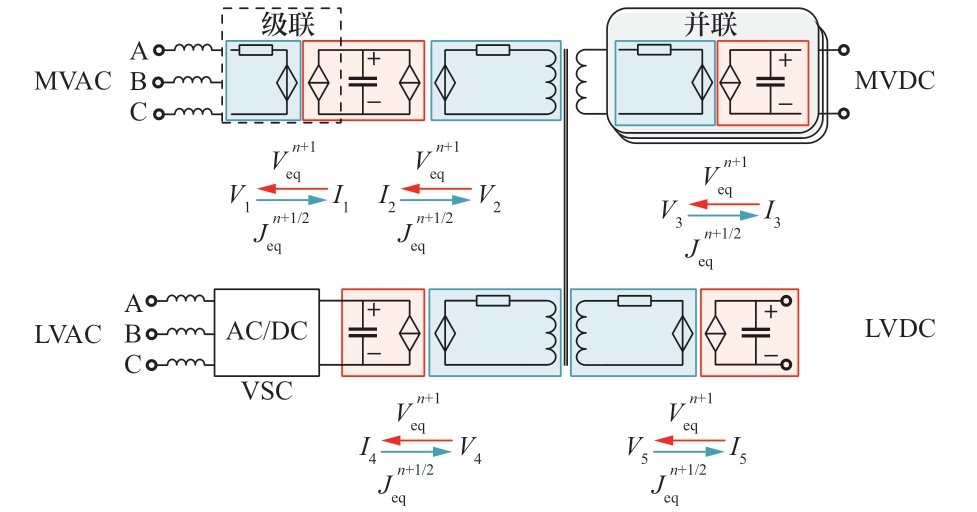
图13 基于MAB多端口拓扑解耦电路图
Fig.13 Decoupling circuit diagram of MAB-based multi-port topology

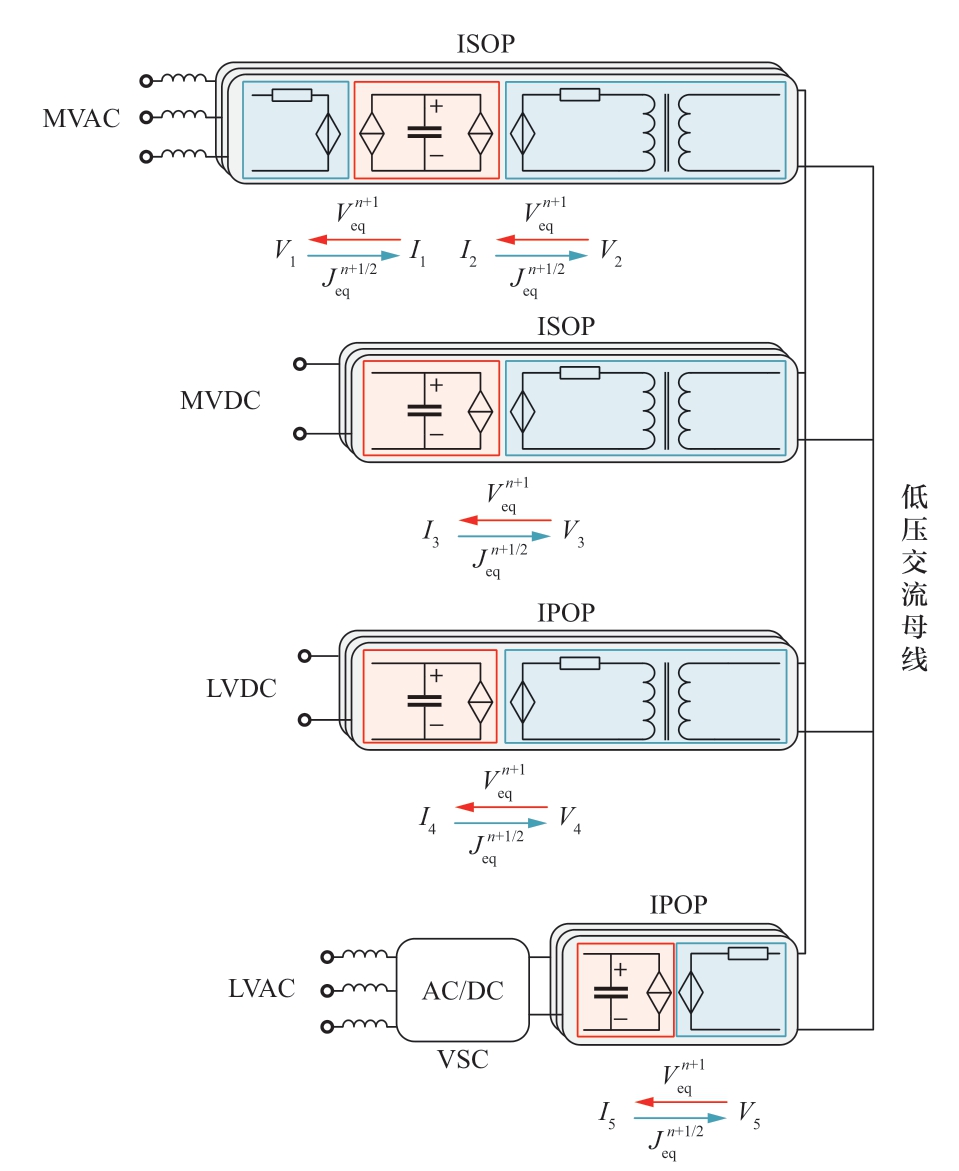
图14 星型共高频链多端口拓扑解耦电路图
Fig.14 Decoupling circuit diagram of star-shaped common high-frequency chain multi-port topology

3 计算时序与流程

3.1 计算时序

按照第2章提出的方法对能量路由器进行解耦，根据等值电路中受控源类型的不同，可以将状态变量分为2个部分。其中x1、x2分别表示受控电压源与受控电流源对应的模块。对于这2组状态变量，根据SILDP原理，二者在时间上交替进行求解，彼此间隔Δt/2，实现图15中的并行计算。

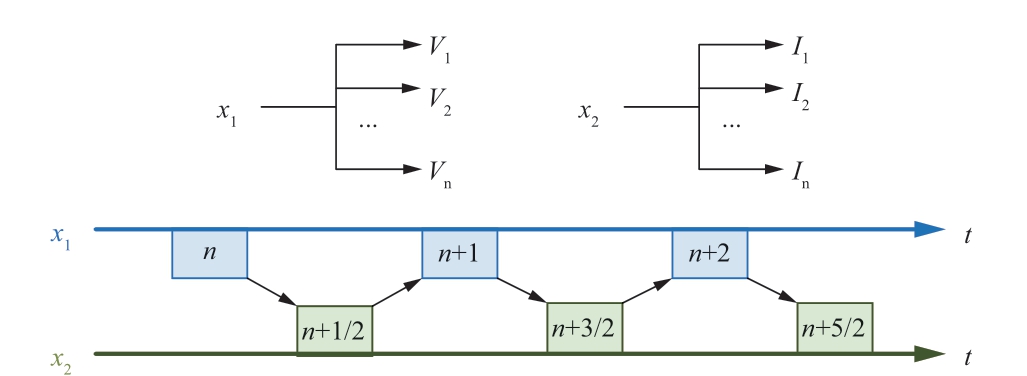
图15 并行计算时序
Fig.15 Timing sequence diagram of parallel computing

3.2 计算步骤

对给定的能量路由器，按上述方法解耦并按状态变量（电感电流和电容电压）进行分组，形成受控电流源和受控电压源2组子系统。设当前时刻为tn，其仿真计算步骤如下。

1）基于半隐式延迟解耦方法，利用半个步长前得到的受控电流源（即），求解当前时刻x2组对应模块的电容电压，结合开关状态，利用式 （5） 计算电压的值。

2）利用，对同一时刻对应x1组状态变量的电感电流进行求解。

3）利用式（5）计算x2组子模块中的电流源，进而对tn+1时刻的x2组进行求解。

4）如果仿真还未结束，则回到第1步开始下个步长的求解，反之则停止计算。

4 解耦模型特点

1）换流器的平均值模型与动态相量模型仅计及设备的外特性，开关函数模型直接忽略开关损耗。此外，平均值、动态相和开关函数3种模型的交流侧与直流侧之间都存在强烈的耦合关系。本文提出的解耦模型解决了这些问题，在保证仿真速度的同时，超过以上3类模型的精确度。

2）将ER按链路级解耦，能够实现各子模块的并行仿真，在很大程度上简化仿真计算的内容。解耦电路中的等效电阻Req=2Ron是固定不变的，随着系统工作状态的更新，只有历史电源Veq，Jeq的值需要重新计算。在整个仿真计算过程中，模型中的导纳是恒定的，仅在仿真的准备阶段生成1次节点导纳矩阵即可，这显著缩短了仿真所需的时间。

3）基于前向欧拉法的传统仿真算法在网络拓扑发生变化时，会出现非状态变量突变的现象，进而导致数值振荡，所以需要改用其他的数值积分方法。本文提出的能量路由器半隐式延迟解耦模型利用矩阵分裂把待求解的状态方程分为2组，在计算中互差半个时间步长，由于状态变量不会突变，可以保留原本的数值积分方法，便于模型的统一与并行计算。半隐式延迟解耦模型选择用中心积分进行离散化，该方法在电磁暂态仿真的时间尺度下，与隐式梯形法有几乎相同的效果，因此第2章提出的等值模型的精确度接近于详细模型。

5 算例验证

编程实现四模块CHB-QAB解耦模型，并将仿真结果与PSCAD/EMTDC中搭建的详细模型进行对比。系统采用ISOP型拓扑，如图16所示。

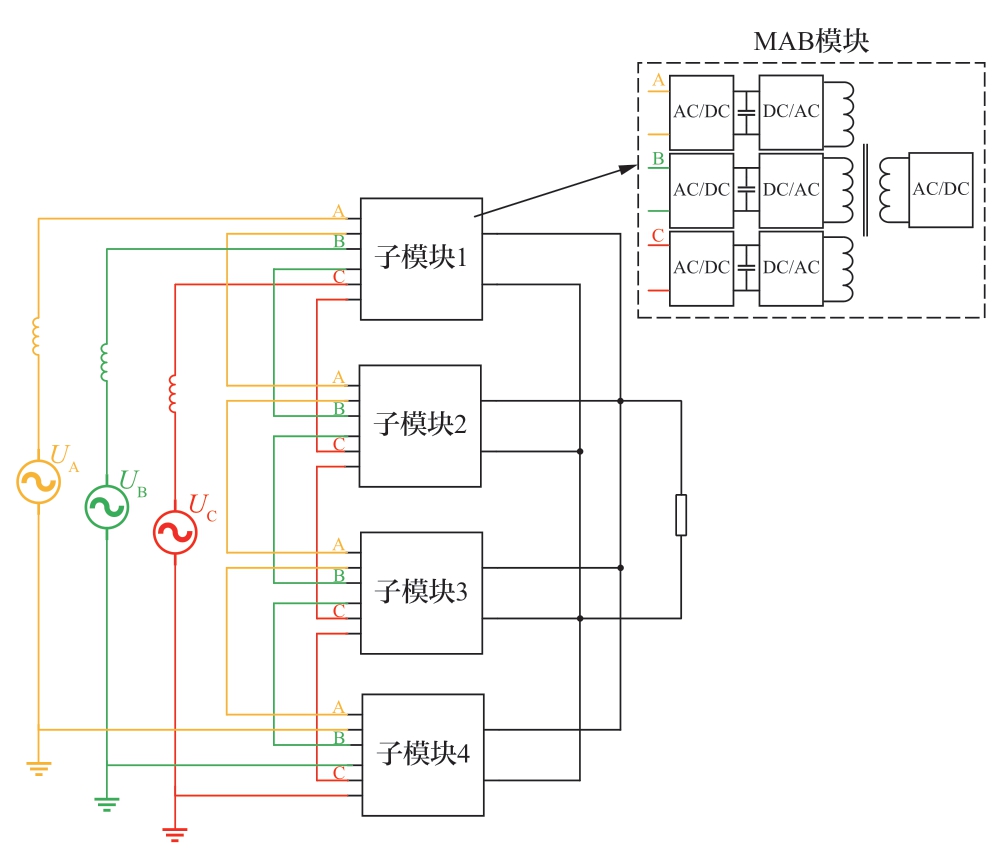
图16 系统拓扑
Fig.16 System topology

测试所用CPU为Intel(Core) 8核i7-10875H，仿真步长1 µs，具体参数见表1。

表1 系统参数
Table 1 System parameters

参数 数值交流电源/kV 40直流负荷/Ω 4 MAB开关频率/kHz 10级联H桥开关频率/kHz 1高压侧电容/F 0.01低压侧电容/µF 500 MAB内电感/µH 100 MAB变比N 1∶1交流侧电抗/mH 6

5.1 仿真精度

基于PSCAD/EMTDC仿真平台，将本文提出的半隐式延迟解耦模型与由分立元件所搭的模型进行比较，图17为模型对比结果。子模块输入侧和输出侧的电压波形如图17 （a） 和 （b） 所示。变压器一次侧和二次侧的电压波形如图17 （c） 和 （d） 所示。图17（e）和 （f） 表示变压器二次侧直流母线电压和负荷电流的波形。

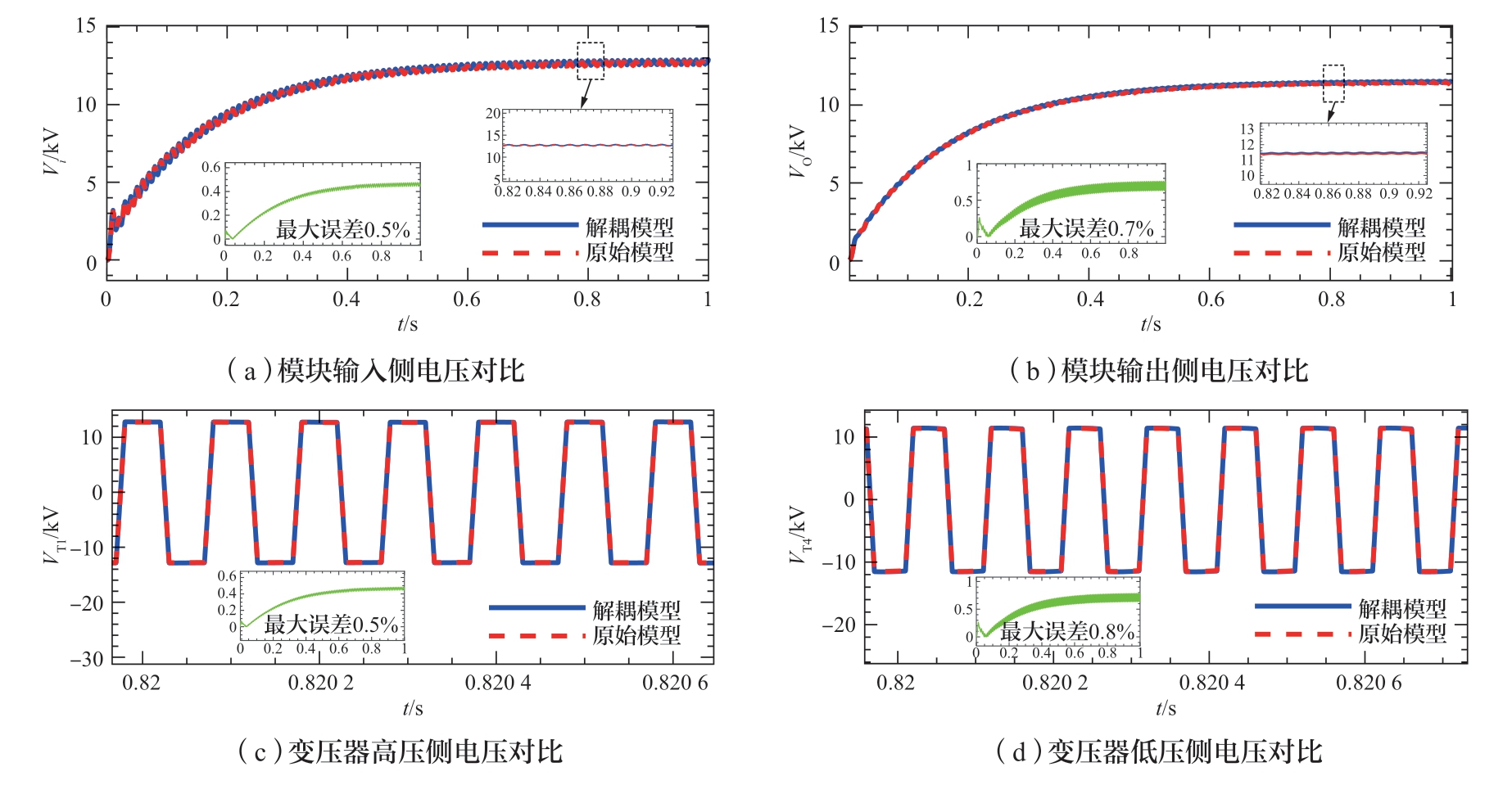
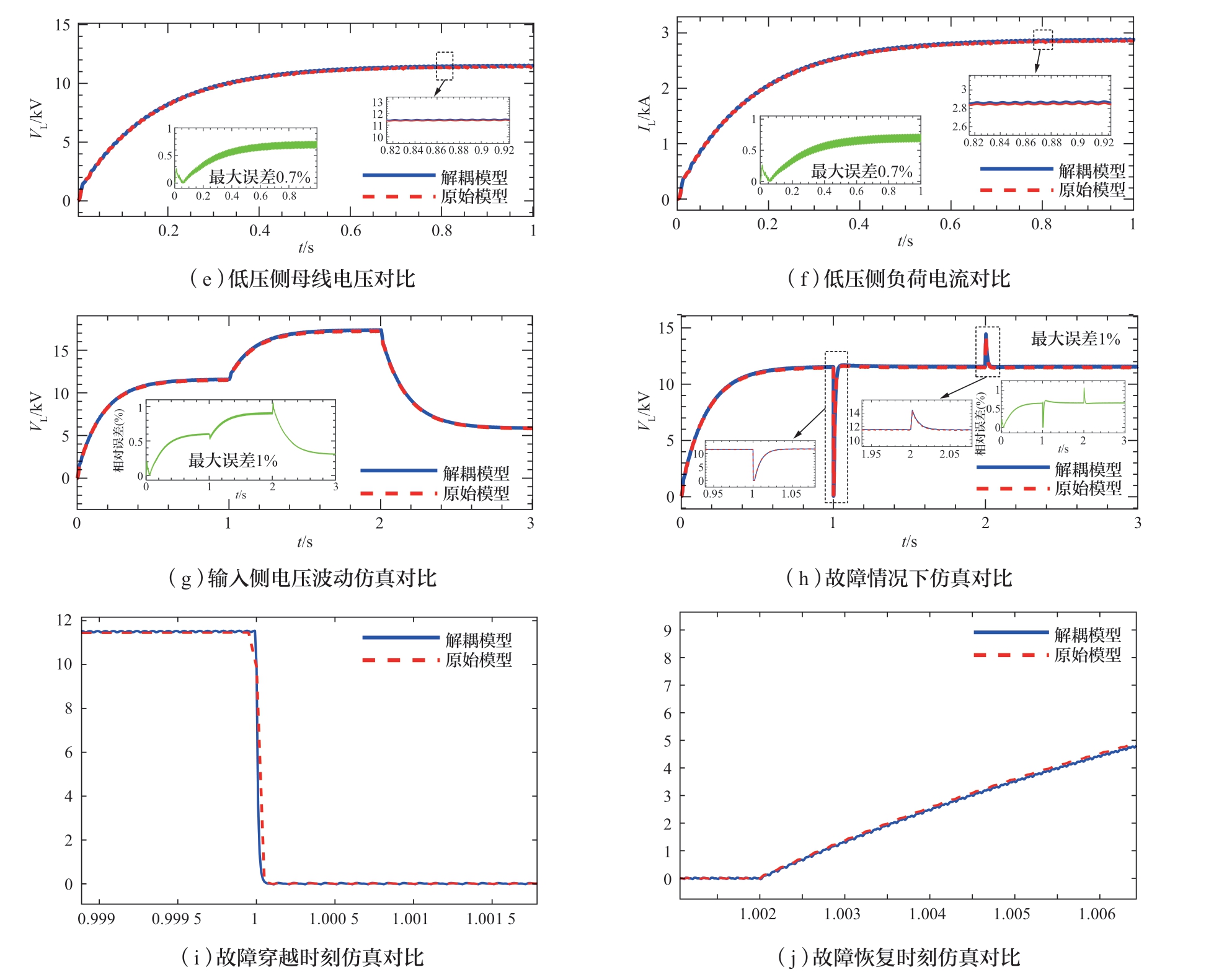
图17 仿真结果波形对比和相对误差
Fig.17 Simulation result waveform comparison and relative error

图17 （g） 表示设备输入侧电压变化时，输出侧电压VL的波形，总时长为3 s。0～1 s，输入侧电压初始值10 kV，仿真开始后逐渐进入额定运行状态；2 s时提高至15 kV，持续时间为1 s；3 s时降低至5 kV，到仿真结束为止。

图17 （h） 表示输出侧直流线路发生故障，输出侧电压VL的波形，负载为4 Ω，总时长为3 s。0～1 s，仿真开始后逐渐进入额定运行状态；1 s时输出侧直流线路发生短路故障，2 ms后故障恢复；2 s时发生断线故障，2 ms后故障恢复，到仿真结束为止。图17 （i） 和图17（j） 分别为短路故障穿越时刻与恢复时刻的输出侧电压波形。

对比以上仿真波形，本文提出的半隐式仿真模型在各种工况下都具有与分立元件模型十分接近的计算结果，二者的相对误差始终不超过1%，这表示前者在精确度方面符合电磁暂态仿真对模型的需求。

5.2 仿真效率

基于PSCAD/EMTDC仿真平台，建立各种规模的CHB-QAB详细模型，模块数依次为4、10、20、40、80、100，同时建立相同规模的解耦等效模型（equivalent decoupling model，EDM），并对解耦模型分别进行串行与并行计算，对比不同算法耗费的时间，以此比较各自的仿真效率，如表2所示。对于仿真相关参数的设置，总的仿真时长取0.5 s，时间步长取1 µs，令QAB开关频率为10 kHz。

表2 不同子模块个数CPU耗时对比
Table 2 CPU time consumption comparison under different numbers of submodules

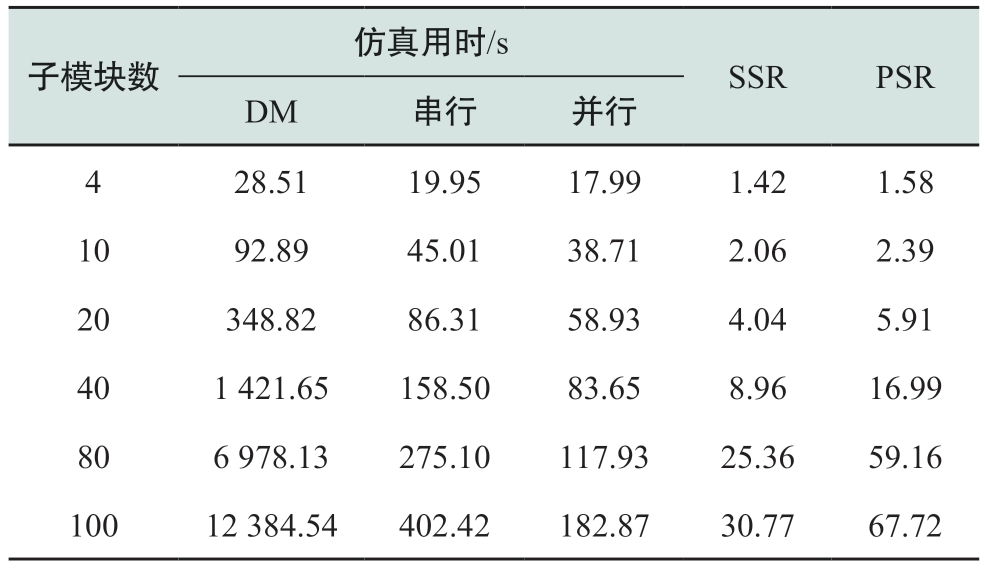
子模块数仿真用时/s SSR PSR DM 串行 并行4 28.51 19.95 17.99 1.42 1.58 10 92.89 45.01 38.71 2.06 2.39 20 348.82 86.31 58.93 4.04 5.91 40 1 421.65 158.50 83.65 8.96 16.99 80 6 978.13 275.10 117.93 25.36 59.16 100 12 384.54 402.42 182.87 30.77 67.72

不同时间步长下的CPU耗时对比如表3所示，不同开关频率下的CPU耗时对比如表4所示。其中，将DM仿真耗费的时间与EDM采用串行计算仿真耗费的时间的比值，命名为SSR（serial speedup ratio），而对于DM仿真耗费的时间与EDM采用并行计算仿真耗费的时间的比值，则命名为PSR（parallel speedup ratio）。

表3 不同仿真步长CPU耗时对比
Table 3 CPU time consumption comparison of models under different simulation steps

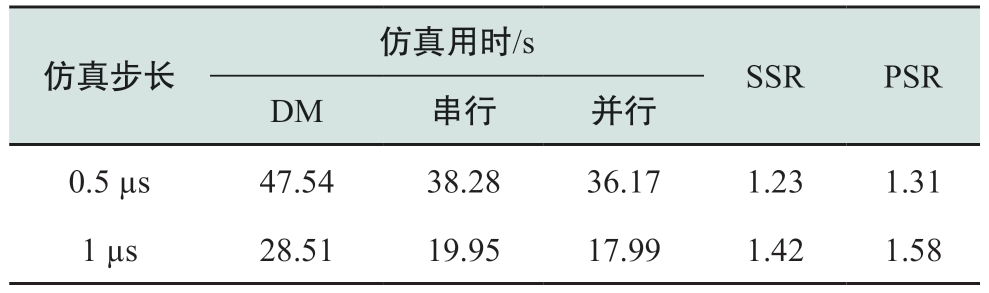
仿真步长仿真用时/s SSR PSR DM 串行 并行0.5 µs 47.54 38.28 36.17 1.23 1.31 1 µs 28.51 19.95 17.99 1.42 1.58

表4 不同开关频率CPU耗时对比
Table 4 CPU time consumption comparison of models under different switching frequencies

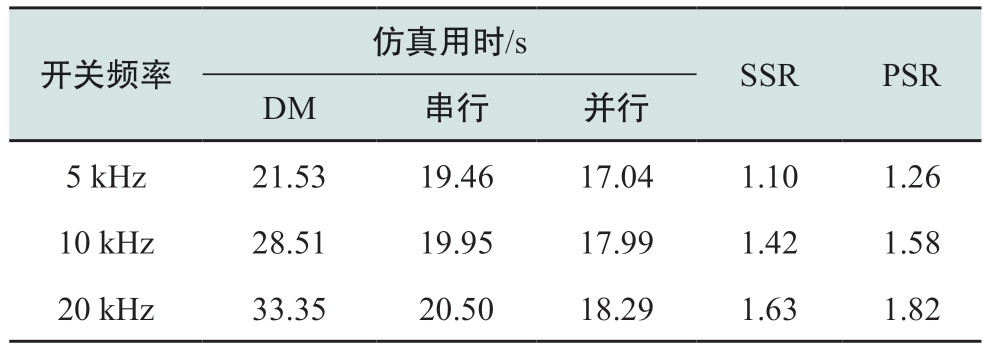
开关频率仿真用时/s SSR PSR DM 串行 并行5 kHz 21.53 19.46 17.04 1.10 1.26 10 kHz 28.51 19.95 17.99 1.42 1.58 20 kHz 33.35 20.50 18.29 1.63 1.82

通过观察表2—4中的数据可以得出结论，本文提出的能量路由器半隐式延迟解耦模型可以明显地提高仿真效率与计算速度，这一加速作用针对各种规模与时间尺度的系统，以及开关频率各不相同的仿真场景都是有效的。此外，对于规模较大的系统，并行计算对仿真效率的提高作用相对于串行计算更为显著。本文的仿真算例由8核心CPU进行计算，如果使用性能更好的CPU或GPU，可以获得更明显的加速效果。

6 结论

本文基于半隐式延迟解耦电磁暂态仿真方法，先列写系统状态方程，推导出H桥的解耦电路，端口电能变换解耦拓扑，根据原始模型推导出不同类型能量路由器的解耦模型，最后以多模块CHB-QAB为例进行了算例验证并给出计算流程。

详细模型与半隐式解耦模型的算例对比结果表明，本文的解耦模型兼具高仿真精度与效率，模块数量和仿真加速比呈正相关趋势，即系统的模块数越多，仿真加速比越大。

本文提出的解耦算法将设备的状态方程分解为2个子系统，不仅降低了矩阵运算的阶数，还实现了子模块之间的并行仿真，使仿真速度显著加快。而且等值后得到的解耦模型是恒导纳模型，省去了当系统运行状态发生改变时，反复计算节点导纳矩阵并进行LU分解的步骤，系统状态的更新在模型中的受控电压源与电流源中得以体现，这也大幅度提高了计算效率。由于不会产生非状态量突变带来的数值振荡问题，避免了解耦后的子系统之间进行算法切换，从而实现解耦形式，仿真的细粒度以及并行的高度一致性。

本文所提出的模型兼具精度和速度的优势，对于包含隔离型、模块化和高频链的能量路由器，其模块数和变换链路级越多，越能凸显该模型的优势，为目前应用中的能量路由器模型规模庞大、结构复杂、计算效率低等缺点的改进提供了有效途径。