0 引言

新能源的大量并网对储能设备提出了更高的要求[1-2]，而抽水蓄能作为技术成熟、经济性好的储能技术[3-4]，成为了提升新能源消纳率，保障电网安全稳定性的关键设备[3]。其中，又以全功率变速抽蓄机组运行模式最为灵活，整体性能最为优异，进而成为国家大力扶持的对象[7]。

按变流器所控制的物理量，可将全功率变速抽蓄机组划分为I型机组与II型机组[8]。I型机组采用变流器控制电磁功率，调速器控制转速的模式，能够快速实现功率的调节[9]，但该类机组中水锤效应将直接作用于轴系[10]，这导致其在出力调节过程中将发生转速反调及导叶超调2个固有现象，存在一定的轴系损伤甚至机组失稳隐患[11-12]。II型机组采用变流器控制转速，调速器控制功率的模型，虽然能够实现机组稳定性及整体效率的提升，但功率调节以s为单位[13]，这在一定程度上限制了机组对新能源的消纳能力及对电力系统的支撑能力。综上，从电网的视角出发，I型全功率变速抽蓄机组更具发展价值，因此需要对该类机组调速系统的稳定性开展研究。

目前学界关于I型全功率变速抽蓄机组调速系统稳定性的研究尚处于起步阶段，但在传统定速抽蓄机组及双馈变速抽蓄机组领域的相关研究能够为本文提供一定的参考。文献[14]建立了传统水电机组调速器小信号模型，并推导了其稳定域的解析表达式，文献[15-16]分别建立了II型双馈变速抽蓄机组机电/电磁暂态小信号模型，并讨论了其对电网频率特性的影响，文献[17]虽建立了I型全功率变速抽蓄机组电磁暂态小信号模型，但对机组稳定性影响因素的分析尚不够充分。

I型机组采用恒功率控制，该环节本身即为非线性环节，因此通过小信号模型分析机组稳定性可能存在一定的偏差，需要与非线性模型进行进一步的对比分析。Hopf分岔理论是分析非线性系统稳定性的重要手段，在水电机组稳定性的分析中也有一定的应用。文献[18-19]将Hopf分岔理论应用于常规水电机组调速系统的稳定性分析中，文献[20]建立了双馈抽蓄机组非线性模型，并计算了不同控制策略下机组稳定域的基本模态，文献[21-22]则在此基础上简要分析了机组各参数对稳定域的影响。然而，机组各参数对其非线性稳定域的具体影响尚不清晰，且由于Hopf分岔的计算量较大，仍希望在小信号模型适用时沿用线性模型的分析结果，而目前研究对于非线性模型及小信号模型适用范围的讨论尚属空白。

据此，本文旨在建立I型全功率变速抽蓄机组的非线性模型，推导非线性视角下机组的稳定域，并详细分析机组各参数对非线性稳定域的影响。进一步地，本文将探讨机组参数对非线性模型与小信号模型所求稳定域之间偏差的影响，并分别给出2类模型的适用范围。

1 I型全功率变速抽蓄机组非线性模型

I型全功率变速抽蓄机组整体模型如图1所示，其包含水力、机械及电气等子模块。本文采用子模块建模方法，在建立各模块机电暂态模型的基础上整合得到机组整体模型。本文旨在分析机组有功功率调节过程中调速系统的稳定性，考虑到模型的时间尺度，首先做出如下假设或说明：

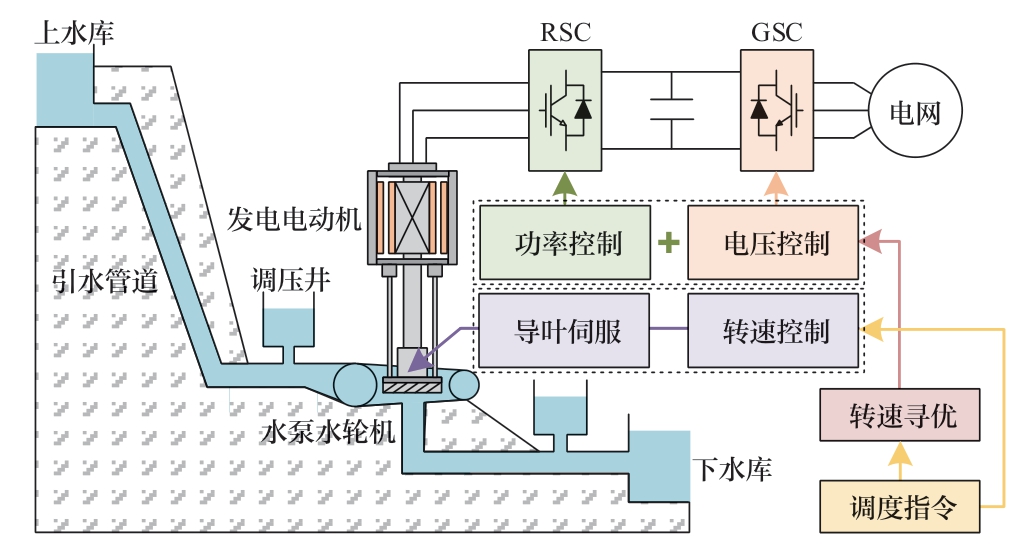
图1 I型全功率变速抽蓄机组结构
Fig.1 Structure of type-I full-power VSPS

1）忽略暂态过程中直流母线电压变化；

2）由于能量流动方向的单一性，将变流器电压-电流双闭环控制简化为单电流环控制；

3）暂不考虑机组参与无功功率调节的情况；

4）暂不考虑控制器的死区及限幅环节；

5）只考虑机组运行在水泵水轮机高效区的情况；

6）后续建模均采用标幺制单位。

水力子系统主要包含引水管道及水泵水轮机，用于实现水流的重力势能到机组转子动能间的能量转换。引水管道提供水流流通的通路，考虑水头损失情况下，其方程如式（1）所示。

式中：h代表水头的偏差量；q代表流量的偏差量；Tw为水锤效应时间常数；kq为水头损失系数。

目前学界尚未提出水泵水轮机的解析模型。然而在高效区内，可以用式（2）所示的6参数模型来近似描述水泵水轮机的转矩及流量特性。

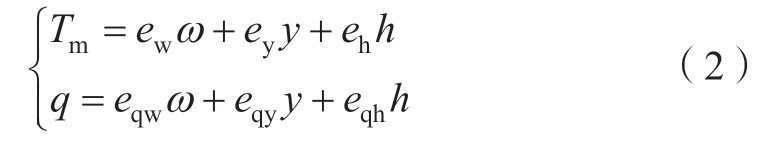
式中：ω为机组转速的偏差量；Tm为机组机械转矩的偏差量；y表示导叶开度的偏差量；ew、eh、ey、eqw、eqh、eqy分别代表水泵水轮机的6个传递系数。

机组的机械子系统包括调速器及转子运动方程。在功率优先控制中，调速器控制框图如图2所示，其通过伺服电机控制导叶开度来实现机组转速的调节。调速器的状态方程如式（3）所示[33]。

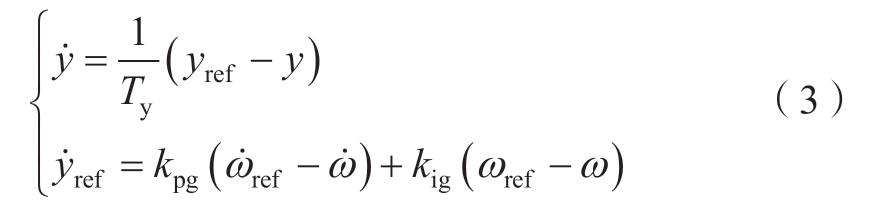
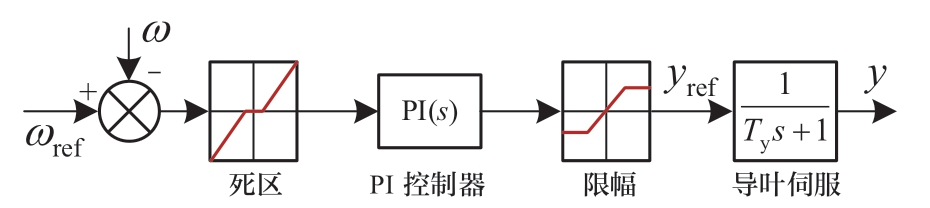
图2 调速器控制框图
Fig.2 Governor control block diagram

式中：Ty代表导叶动作时间常数；kpg与kig代表调速器控制参数。

机电暂态下采用一阶转子运动方程即可，如式（4）所示。

式中：Tem代表电磁转矩的偏差量；TJ代表机组惯性时间常数；D代表机组阻尼系数。

电气子系统包括转速寻优环节及全功率变流器。水泵水轮机在水头及出力一定时，存在一个使其效率最高的转速点，即最优转速。转速寻优环节的作用即为根据机组出力指令及当前水头计算最优转速，由文献[8]可知，最优转速与功率指令和水头近似呈线性关系，且斜率与工作水头几乎无关。忽略暂态过程中水头的变化，最优转速偏差量与功率指令偏差量之间的关系可简写为式（5）。

全功率变流器分为机侧及网侧2部分，其中机侧变流器通过开关管的动作调节机组电磁功率，而网侧变流器用于维持直流母线电压。基于前述简化假设，不考虑网侧变流器及电压外环动态特性的情况下，全功率变流器的控制框图如图3所示[24]。在标幺制下，iq与Tem有相等的数值，此外，机侧变流器可简化为时间常数为Tc的惯性环节，因此全功率变流器的状态方程如式（6）所示。

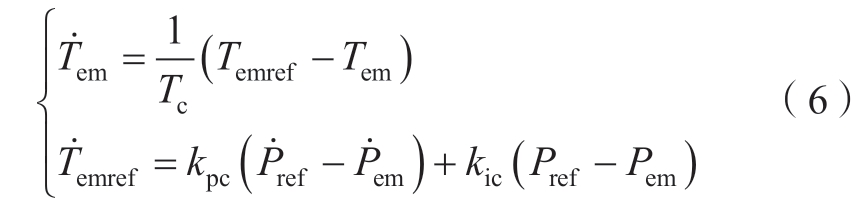
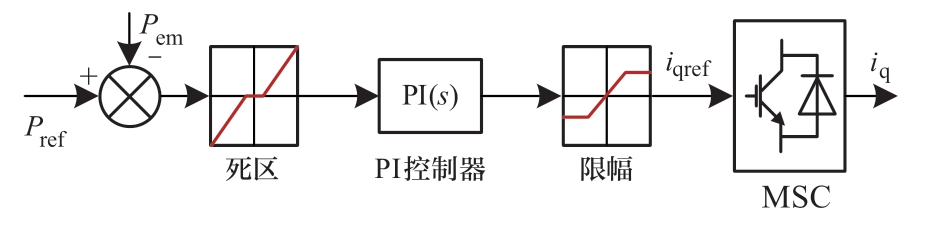
图3 变流器控制框图
Fig.3 Converter control block diagram

式中：kpc与kic代表变流器控制参数。

机组电磁功率偏差的计算式如（7）所示，其中ωn与Temn分别代表转速与电磁转矩基准值，此处均取为1。而在小信号模型中二阶项可以忽略，进而式（7）式可以简化为式（8）。

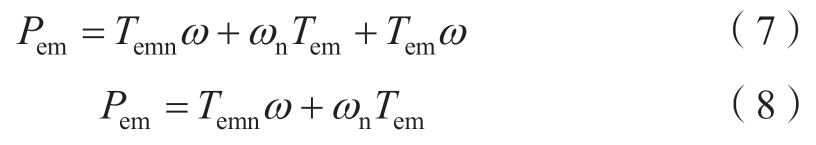
式（1）—（7）构成了I型全功率变速抽蓄机组非线性模型，将式（8）替代式（7）则构成机组的小信号模型。由于Tc是一个很小的数值，因此可以认为电磁功率能够立即跟踪功率指令，据此可以将非线性模型降阶到4阶，其状态方程如较为复杂，详见附录A，在后续的分析中均采用该降阶模型。

如图4所示，利用水泵水轮机的特性曲线及电机的等功率线，以机组功率指令上升为例论述机组潜在的转速失稳风险。出力调节前机组稳定运行于A点，某一时刻功率指令从P0跃升至Pref，此后变流器快速动作将电磁转矩提升至Pref对应的等功率线上，即B点所在位置。此时制动性质的电磁转矩大于驱动形式的机械转矩，因此机组沿等功率线开始减速。然而，由于电机恒功率控制要求转速与电磁转矩的乘积一定，机组减速过程中电磁转矩反倒上升，进一步加剧了减速的趋势，以此类推形成了潜在的正反馈过程。若调速器动作及时，即机械转矩沿AC变化，则在C点处机组停止减速。随后在调速器控制机组，电磁转矩沿等功率线经CBD达到D点，完成出力的调节。而若调速器不能及时动作，则由于正反馈的存在，转速将一直下跌直至机组失稳，如图中曲线BE、AF所示。

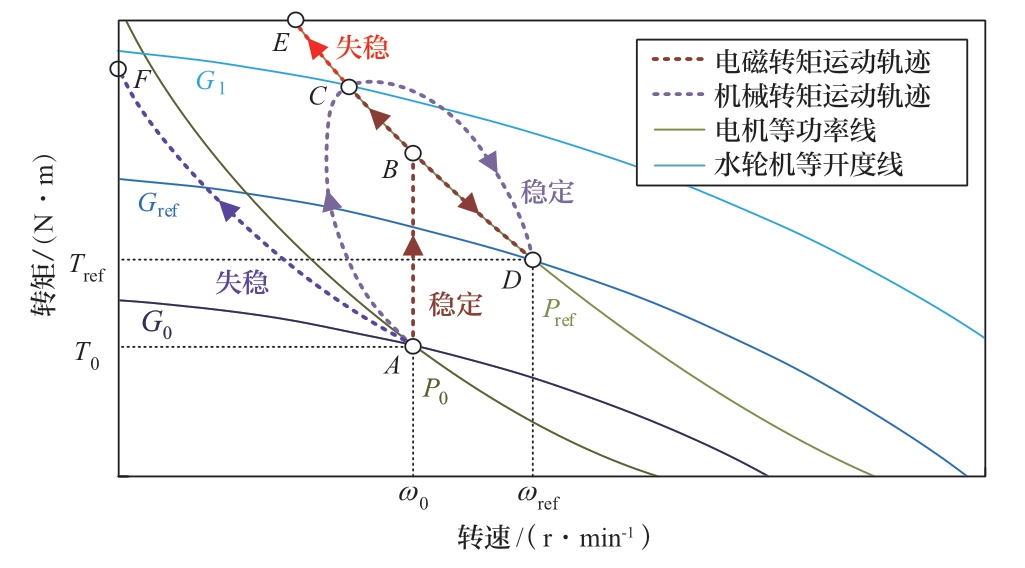
图4 机组出力调节过渡过程轨线图
Fig.4 Trajectory diagram for the transient process of unit output regulation

综上所述，转速的反调及导叶的超调均是功率优先控制下全功率变速抽蓄机组的固有特性，也是机组调速系统稳定性风险的外在表现。接下来，本文将利用Hopf分岔理论分析非线性条件下机组调速系统稳定域特征及其主要影响因素。

2 基于Hopf分岔理论的机组稳定性分析

2.1 Hopf分岔理论

Hopf分岔是非线性动力系统中常见的现象，即当某个参数μ（称为分岔参数）变化到某一临界值μc时，系统的平衡点发生稳定性的转变，并产生一个极限环。即系统从一个稳定的平衡态转变为周期性振荡状态。

Hopf分岔又可分为超临界分岔和亚临界分岔两类，如图5所示。当系统发生超临界分岔时，系统平衡点将从一个稳定的结点变为一个被稳定的极限环包围的不稳定结点，即系统从平衡状态进入一个稳定的周期性振荡状态。而当系统发生亚临界Hopf分岔时，围绕稳定结点的不稳定极限环将逐步向内收缩，直至将稳定的结点变为不稳定的结点，即系统从平衡状态进入一个发散振荡状态[25]。

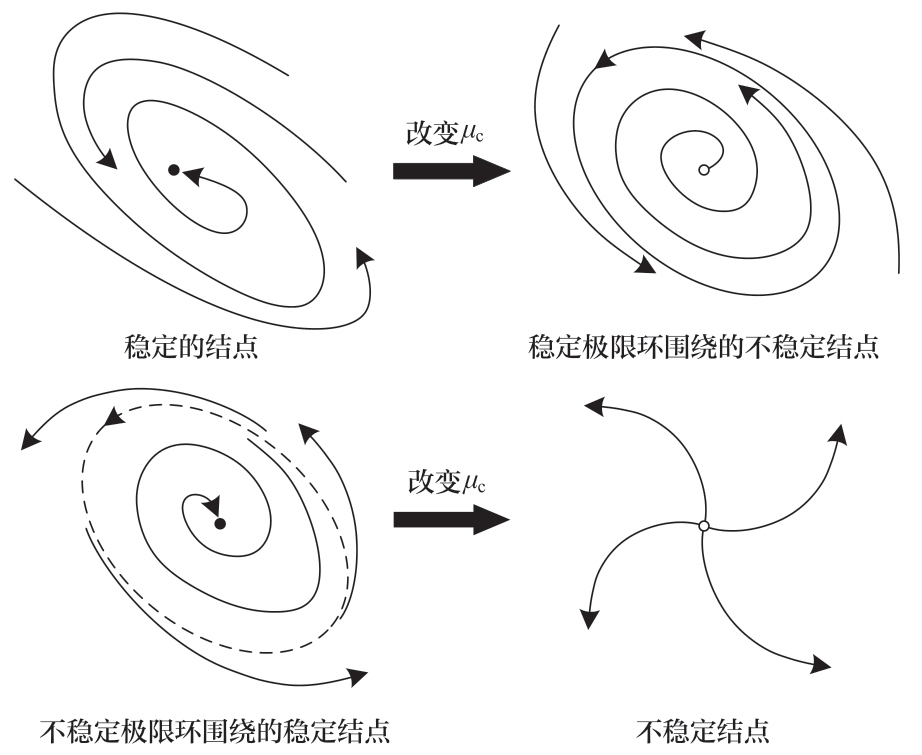
图5 超临界分岔与亚临界分岔
Fig.5 Supercritical bifurcation and subcritical bifurcation

判断Hopf分岔及其形式的方法如下：

1）计算系统的稳定点；

2）计算状态方程在稳定点附近的雅可比矩阵；

3）求雅可比矩阵特征方程有纯虚数根时对应的μc值；

4）按式（9）计算分岔点的横截系数

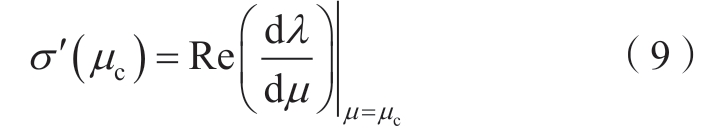
如果σ'大于0，则发生亚临界分岔，反之则发生超临界分岔。

2.2 机组稳定性分析

首先计算机组的平衡点，当功率指令为Pref时，系统的平衡点S记为式（10），其具体值较为复杂，详见附录A。需要注意的是，这里的平衡点指机组功率指令改变后系统新的不动点。

附录 A I型全功率变速抽蓄机组非线性模型

I型全功率变速抽蓄机组的四阶状态方程较为复杂，为了模型的简化，首先定义：

机组状态方程如式（A2）所示。

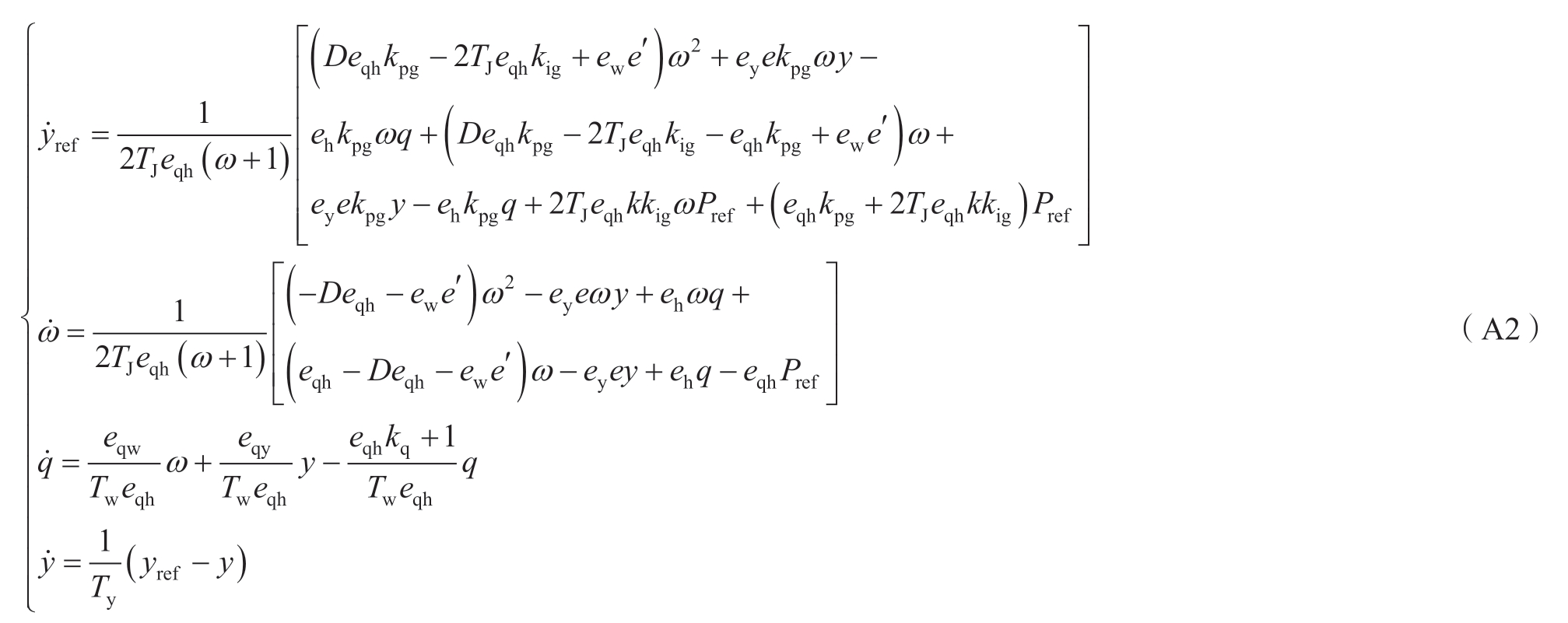
机组平衡点S的坐标为：

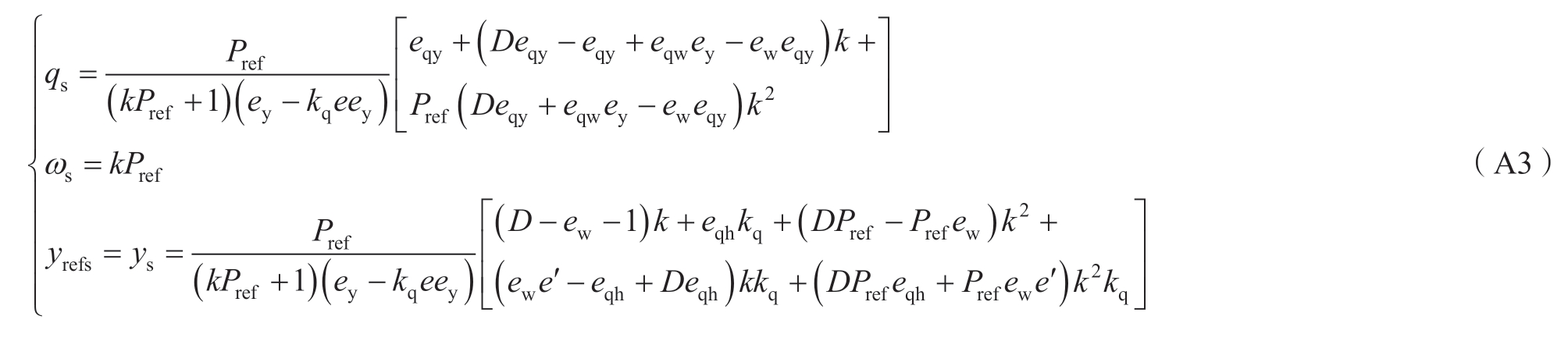
将机组在S点附近线性化，并求出状态方程在该点处的雅可比矩阵J如式（11）所示。

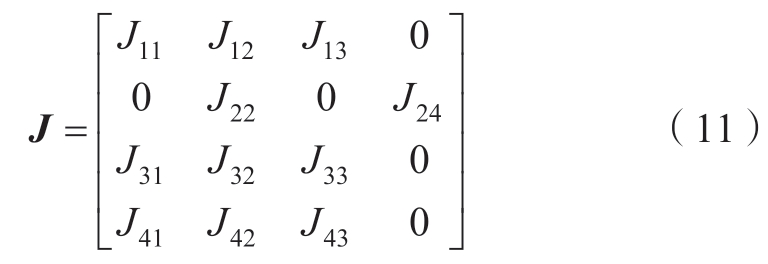
J矩阵的特征方程如式（12）所示。

其分岔点处横截系数的计算如式（13）所示。

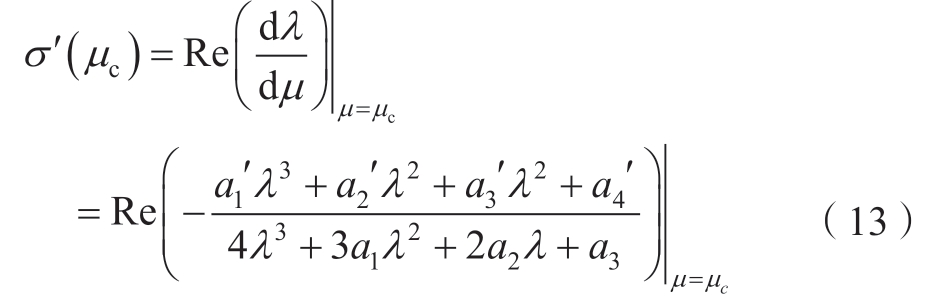
其中：

以春厂坝全功率变速抽蓄机组[7]为例，其关键参数如表1所示。以kpg为自变量，kig为分岔参数，在改变kpg时计算分岔发生时的kig值如图6所示，曲线与坐标轴围成的蓝色区域即为机组调速系统的稳定域。

表1 机组典型参数
Table 1 Typical unit parameters

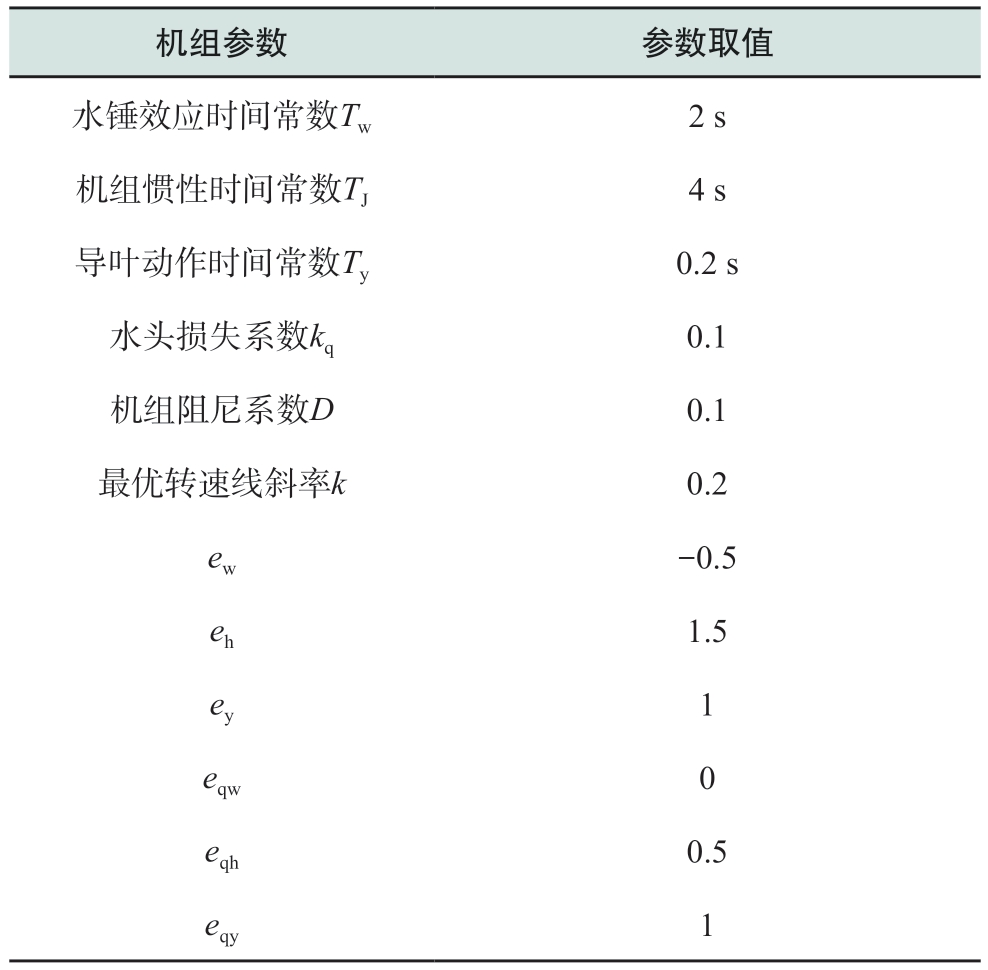
机组参数 参数取值水锤效应时间常数Tw 2 s机组惯性时间常数TJ 4 s导叶动作时间常数Ty 0.2 s水头损失系数kq 0.1机组阻尼系数D 0.1最优转速线斜率k 0.2 ew -0.5 eh 1.5 ey 1 eqw 0 eqh 0.5 eqy 1

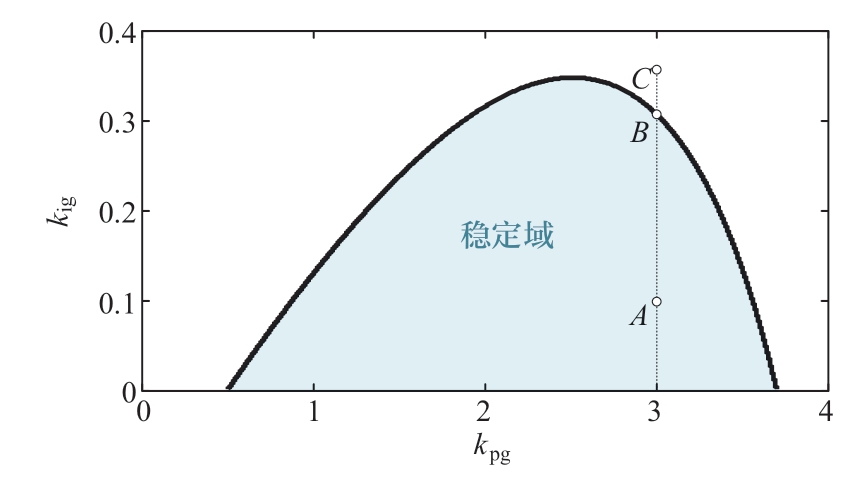
图6 机组非线性模型稳定域
Fig.6 Stability domain of the unit nonlinear model

计算分岔点对应的横截系数，结果如图7所示，由图可知，机组横截系数始终大于0，分岔类型始终为亚临界分岔，即当kig越过分岔点时，机组将从平衡状态直接进入一个发散振荡状态。

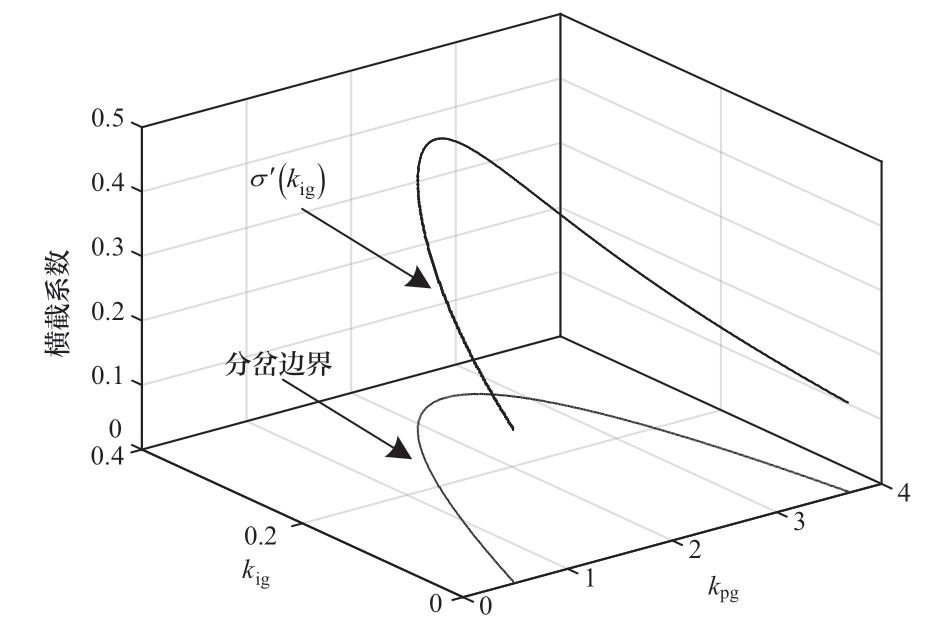
图7 分岔点横截系数
Fig.7 Cross-section coefficient of bifurcation point

2.3 仿真及实验验证

沿用表1数据，出力调节前机组工作于额定功率点，在t=0 s时功率指令上升5%，绘制图6中A、B、C 3点处机组转速及功率的变化情况，结果如图8所示。由图可知，机组在A点 （稳定域内） 转速收敛到最优转速值，在B点 （分岔边界） 转速发生等幅振荡，而在C点（稳定域外）转速发生发散振荡，这与前述分析是一致的。

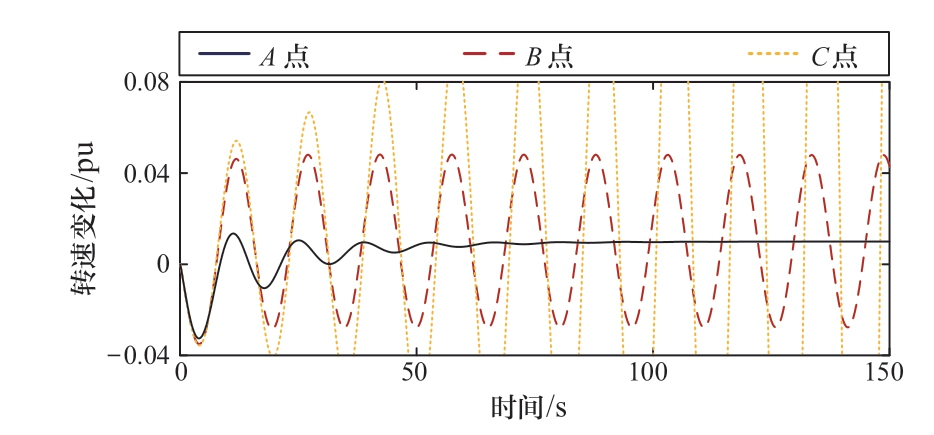
图8 各点处机组转速变化规律
Fig.8 Variation of unit speed at different points

为进一步验证分析结果的准确性，基于文献[8]中给出的I型机组电磁暂态模型，并结合如图9所示的RT-lab控制在环实验平台对分析结果进行进一步的验证，实验参数详见附录B。得到图6中A、B、C点对应调速器控制参数下机组出力调节过程中电磁功率，转速与导叶开度的变化情况如图10所示。由图可知，除C点处由于导叶限幅环节导致机组转速变化情况与图8理论分析结果存在一定差异外，式（A2）所述非线性简化模型及其对应的稳定性判据能够较为准确地描述机组出力调节过程中的动态特性及稳定性。

附录 B 机组模型参数表

本文使用的全功率变速抽蓄机组模型其他关键参数如表B1所示。

表B1 机组参数
Table B1 Unit parameters

额定容量 额定转速 额定转矩 电机极对数 工作水头5 MVA 750 r/min 63.7 kN·m 4 200 m直流母线电压机组转动惯量 开关频率 开度额定值 直流母线电容1500 V 6.5 t·m2 10 kHz 20° 5 mF

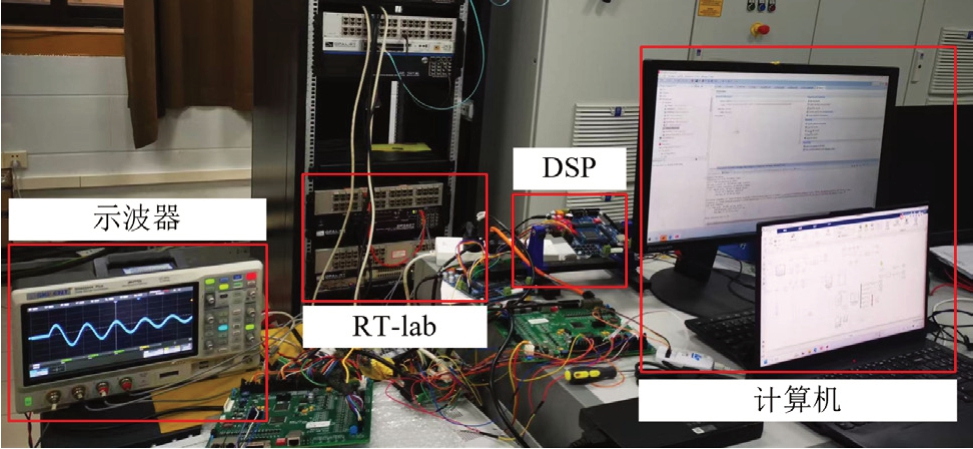
图9 实验平台架构
Fig.9 Experimental platform architecture

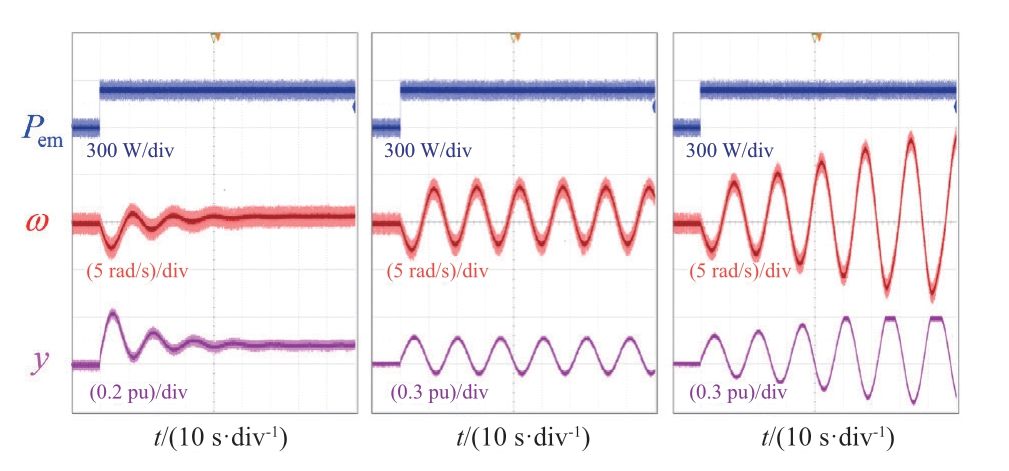
图10 各点实测波形
Fig.10 Measured waveforms at different points

3 机组稳定域影响因素分析

在第2章，本文通过非线性动力学中的分岔理论推导了I型全功率变速抽蓄机组的稳定域。然而，非线性系统的稳定域分析的计算量远大于线性系统，因此有必要分析机组非线性模型稳定域的影响因素，提取非线性系统与线性系统分析结果的主要差异及其成因，并归纳二者的适用范围。

3.1 机组稳定性影响因素

由图4的分析知，I型全功率变速抽蓄机组易发生失稳的根本原因是水力环节与电气环节之间响应速度的差异，因此在简化电气环节后的四阶模型中，水泵水轮机参数成为机组稳定性的主要影响因素。

首先分析水泵水轮机6个传递系数对系统稳定性的影响，在表1所示参数的基础上，分别使各传递系数增加0.1，计算分别采用小信号模型（small signal model，SSM）以及不同功率指令下的非线性模型（non-linear model，NLM）时，机组稳定域面积的变化率，结果如图11所示。由图可知，机组稳定域与ew、eh及eqy成负相关，与eh、ey及eqw成正相关，且受eqy的影响最为显著。此外，在功率指令上升时，非线性模型稳定域对各参数的灵敏度低于小信号模型，在功率指令下降时则相反。

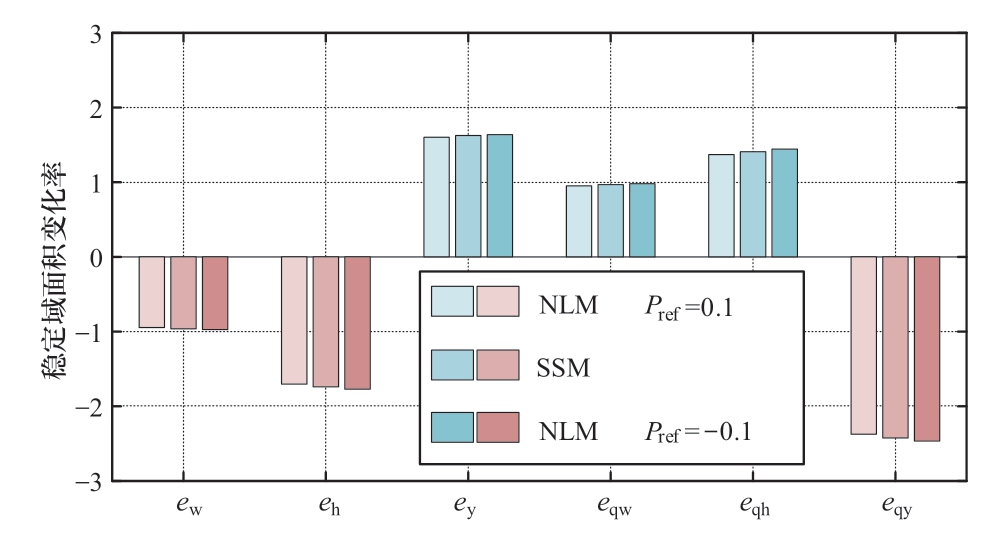
图11 各传递系数对稳定域面积的影响
Fig.11 Impact of each transfer coefficient on the stability domain area

稳定域面积的变化率可以衡量各参数对机组稳定域整体的作用效果，而稳定域边界曲线的具体形态则可以进一步反映各参数对稳定性的影响。此处以Pref=0.05为例，选用稳定域边界曲线与横轴的交点坐标kpgmax、kpgmin及kig能取到的最大值kigmax，结果如图12所示。由图可知，kpgmin主要受ew与ey影响，这是便于由图4直观理解的：由于图4中C点位置受调速器初期动作速度与水泵水轮机等开度线的倾斜程度共同影响，绝对值较大的ew（ew一般为负值）对应倾斜程度较高的等开度线，因而此时较慢的导叶动作速度也能使机组稳定，而较大的ey代表机械转矩对导叶的变化更为灵敏，因此无需较大的kpg也能达到同样的机械转矩输出效果。而相比之下kpgmax与kigmax的影响因素更为复杂，与水泵水轮机6个传递系数均有一定关联，其中，eh与eqy对二者的影响均相对较大。

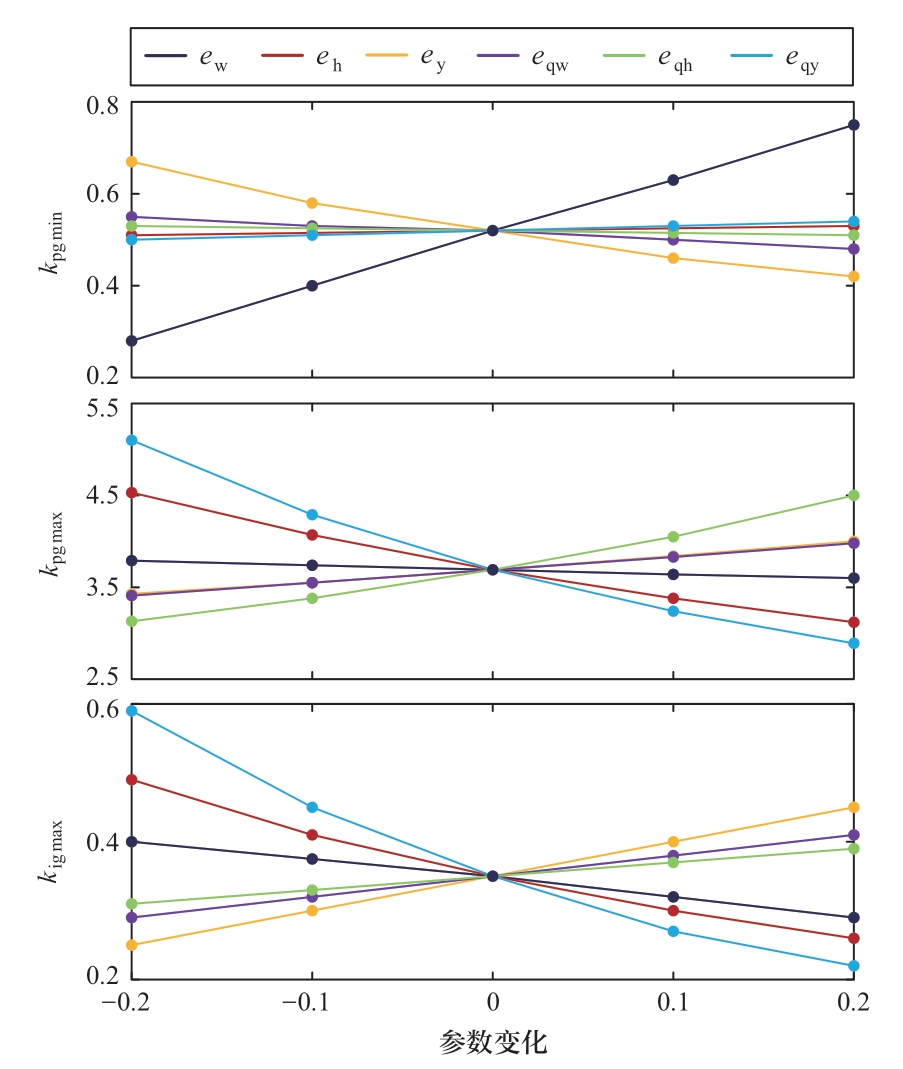
图12 各传递系数对稳定域极值点的影响
Fig.12 Impact of each transfer coefficient on the extreme points of the stability domain

3.2 非线性模型与小信号模型对比分析

与小信号模型不同的是，非线性模型的稳定域与稳定点S的位置有关。而S仅与功率指令及k有关。因此Pref与k的取值是小信号模型与非线性模型之间差异的重要影响因素。

继续沿用表1参数，绘制在不同的Pref及k值下，机组非线性模型及小信号模型稳定域面积差异百分比ΔS的变化情况，结果如图13所示。由图可知，在不同的k值下二者面积差异均呈现如式（15）所示的抛物线关系，即当功率指令下调时，小信号模型稳定域计算结果偏保守，而当功率指令上调时，小信号模型计算结果偏乐观。此外，随着k值的增加，二者面积的差异逐步减小，即小信号模型更适用于宽转速范围的I型全功率变速抽蓄机组的稳定性分析中。

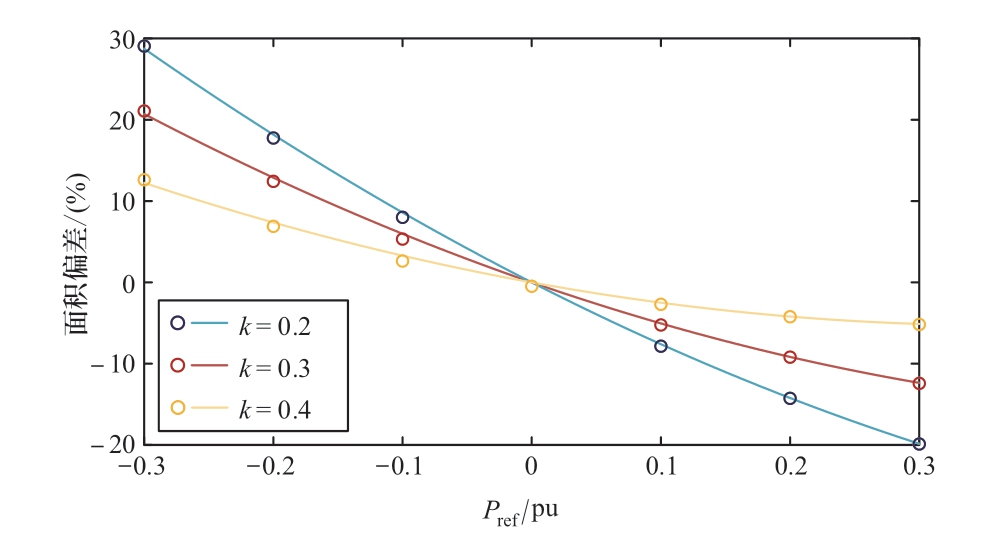
图13 SSM与NLM的偏差程度
Fig.13 Degree of deviation between SSM and NLM

出于计算简便的考虑，在小信号模型稳定域面积大于非线性模型稳定域面积，且二者相差10%以内时，采用小信号模型较为适宜。由上述分析可知，二者稳定域面积的偏差主要与k与Pref有关，在不同的Pref下小信号模型（SSM）的适用范围如图14中蓝色区域所示。由图可知，在功率指令上调时，小信号模型对稳定域的估计均偏乐观，因此应使用非线性模型，而在功率下调幅度较小时，所有的k值下小信号模型与非线性模型的稳定域面积相差均在10%以内，随着功率指令绝对值的增加，小信号模型在k较小时将不再适用。

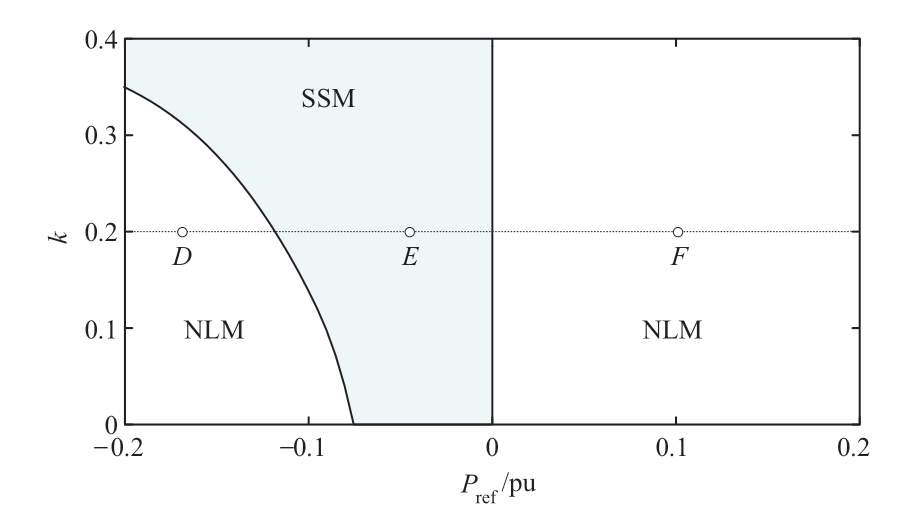
图14 SSM与NLM的适用范围
Fig.14 Applicability of SSM and NLM

在图14中选取D、E、F 3点，取kpg=2.5，kig=0.35，同样基于图9所示实验平台，对比采用SSM及NLM时所得机组转速变化情况与实测波形的偏差程度，结果如图15所示。由图可知，D所在区域中小信号模型对机组稳定性的估计过于保守，F所在区域则会将不稳定的控制参数配合误判为稳定，E所在区域则能在做到不过于保守的同时防止不稳定参数组合的误判，这验证了图14所划分出的小信号模型适用范围的准确性。

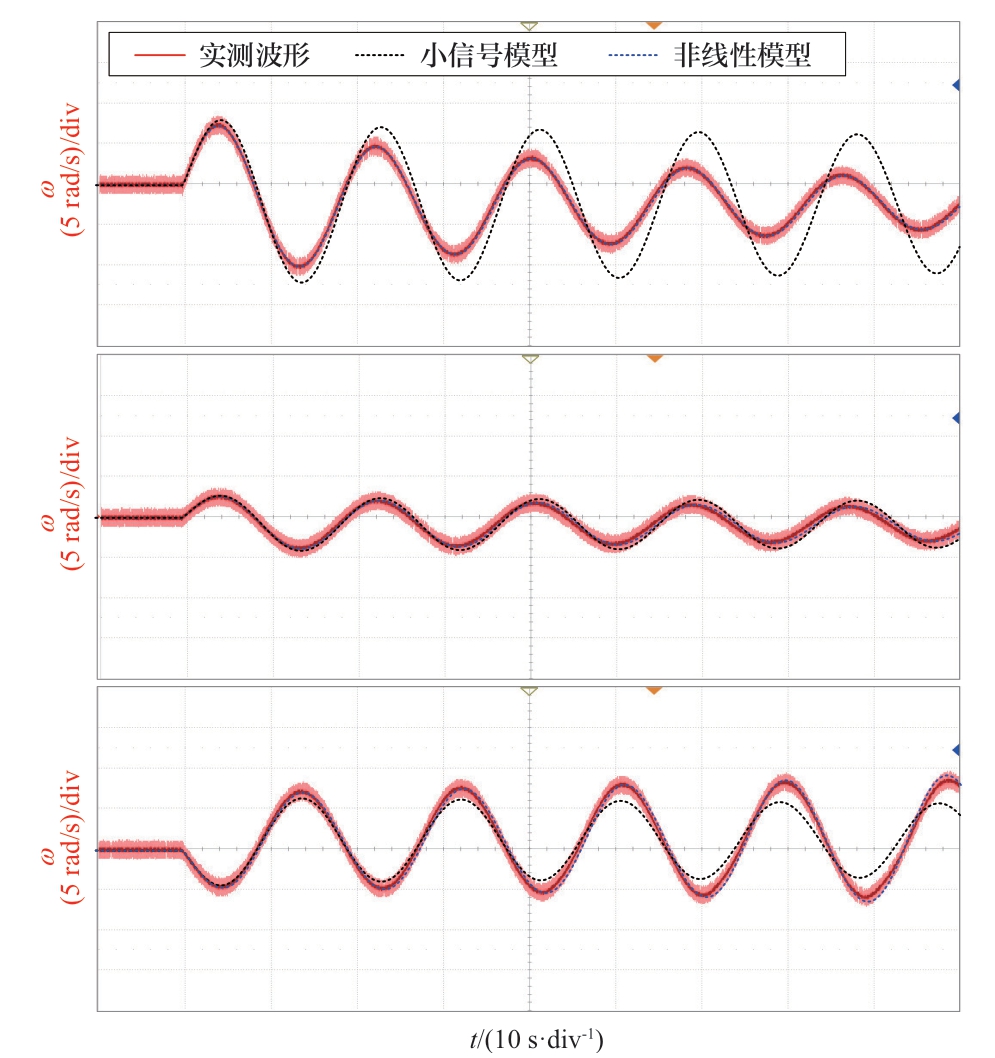
图15 SSM适用范围验证
Fig.15 Verification of the applicability of SSM

4 结论

本文建立了I型全功率变速抽蓄机组非线性模型，推导了非线性视角下机组的稳定域，分析了机组各参数对非线性稳定域的影响及非线性模型与小信号模型间差异的影响因素，最终给出了非线性模型与小信号模型分别的适用范围。根据理论分析及仿真验证，本文可得出以下结论。

1）I型全功率变速抽蓄机组分岔类型为亚临界分岔，即当调速器控制参数超出某一范围时，机组将从稳定直接过渡到发散振荡。机组非线性稳定域中kpg的下界主要与ew与ey有关，kpg的上界与kig的最大值则与6个传递系数均有关。

2）机组小信号稳定域与非线性稳定域之间的差异主要与k与Pref有关，当出力下调时，小信号模型总是偏保守，出力上调时小信号模型则偏乐观。且二者之间的差异与Pref的绝对值成正比，与k成反比。

3）出于计算简明与不发生稳定性误判的原则，在功率下调时采用小信号模型为宜，且当功率下调幅度较大时，k应大于某临界值。其余情况应采用非线性模型进行稳定性分析。