0 引言

随着新能源渗透率的不断提高，电力系统逐渐呈现出高比例可再生能源和高比例电力电子装备的“双高”特性[1]。相比于同步发电机主导的传统电力系统，电力电子装备的低惯性、低短路电流和弱抗扰性使得“双高”电力系统具有非线性、时变性、不确定性和复杂性等动态特性[2]。并网逆变器作为新能源发电的核心装备，承担着能量高效转换的关键任务，其与电网的联接与交互是影响新能源并网发电系统稳定、高效运行的关键因素[3-9]。

随着新能源发电单元对同步发电机组的逐步取代，电网强度不断降低，文献[10]指出，基于锁相环的跟网型逆变器在低短路比的弱电网下容易出现失稳振荡现象。与跟网型逆变器不同，构网型逆变器通过外部功率环生成并网公共耦合点（point of common coupling，PCC），电压幅值与相位参考实现与电网同步，在弱电网下具有更好的稳定性，因此近些年来受到了越来越多的关注。目前，关于构网型逆变器稳定性的研究包括许多方面，其中小信号稳定性已经从不同的方面得到了广泛的研究[11]，近些年来关于构网型逆变器暂态稳定性问题的研究也在逐渐深入：例如文献[12]探究了功率控制参数对构网型逆变器暂态稳定性的影响，并提出了一种暂态阻尼方法，同时提高了系统的同步稳定性和频率稳定性；文献[13]通过构建李雅普诺夫能量函数对构网型逆变器的暂态行为进行描述，并通过修改有功功率参考提高了系统的暂态稳定性。然而，由于构网型逆变器的电压源特性，其输出电流高度依赖于外部系统条件[14]。当电网遭遇故障时，传统的同步发电机可以提供5～7 pu过电流[15]，但基于电力电子半导体器件的构网型逆变器通常只能承受1.2～2 pu过电流[16-17]，这意味着在发生故障时，并网逆变器必须采用适当的限流方法来限制流过逆变器桥臂的电流。

在不改变构网型逆变器基本同步控制结构的情况下，主要有2种限流策略。一种是基于电流饱和算法的限流器，在电网发生严重故障时，通常通过修改电流基准使逆变器处于电流源状态，以满足故障电流的限制要求。另一种是虚拟阻抗法，当逆变器电感电流超过标称值时，通过按比例增加虚拟阻抗来修正电压控制回路参考值。因此，该策略可以在电网故障下保持电压源特性，并在故障清除后自动恢复[18]。文献[19]指出，限流器在故障时刻对电流的抑制能力更好，因此本文将针对限流器开展研究，探究其对构网型逆变器暂态稳定性的影响。文献[20]分析了在优先限流器作用下构网型逆变器的暂态行为，并提出了一种稳定性增强P-f下垂控制策略，帮助构网型逆变器在限流状态下保持稳定。文献[21]表明，将限流器的偏移角与滤波器阻抗和线路阻抗组成的阻抗角对齐，就能最大程度保证逆变器的构网能力。文献[22]发现适当调节限流器的饱和电流相位，能够提高构网型逆变器在限流模式中的瞬态稳定性，并提出了一种动态限流方法，保证构网型逆变器在电网故障下的暂态稳定性与安全性。基于d轴优先限流器，文献[23]揭示了限流保护会改变构网型逆变器的输出功率特性，使得减速面积变小从而减低了暂态稳定性。然而，使用限流器的构网型逆变器在电压源和电流源之间的模式切换逻辑尚未得到广泛研究。文献[24]提出了构网型逆变器在排除电网故障后如何恢复正常运行的标准，但其忽略了无功回路的影响。然而，以上分析研究忽略了故障恢复后的去饱和问题，基于d轴优先限流器的构网型逆变器在遭遇电网故障后仍存在无法恢复正常稳定工作的风险[25]，这将严重影响构网型逆变器的电压源特性。

在此基础上，本文从理论上分析了基于d轴优先限流器的构网型逆变器模式切换逻辑，同时考虑了无功回路的影响。本文的主要贡献如下：①推导了构网型逆变器在不同模式下的稳定边界；②得到了构网型逆变器在正常模式和限流模式之间的模式切换条件；③提出了一种电流抗饱和策略，通过PI控制器限流和虚拟电阻实现故障后限流模式向正常模式的切换，改善了构网型逆变器的电压源特性。

1 构网型逆变器的暂态稳定性与模式切换条件

1.1 系统概述

构网型逆变器的系统拓扑和控制结构如图1所示。Vdc为直流侧母线电压，逆变器通过LC滤波器与电网相连，其中Lf和Cf为滤波电感和滤波电容。根据戴维南定理，电网可以等效成理想电压源与电网阻抗的串联形式，其中Vg为电网电压幅值，Lg和Rg分别为电网线路电感和线路电阻。iLabc、vabc、iabc分别是滤波电感电流、滤波电容电压也即是逆变器输出电压和PCC电压、逆变器输出电流，其在dq坐标系下分别表示为iLdq、vdq、idq。

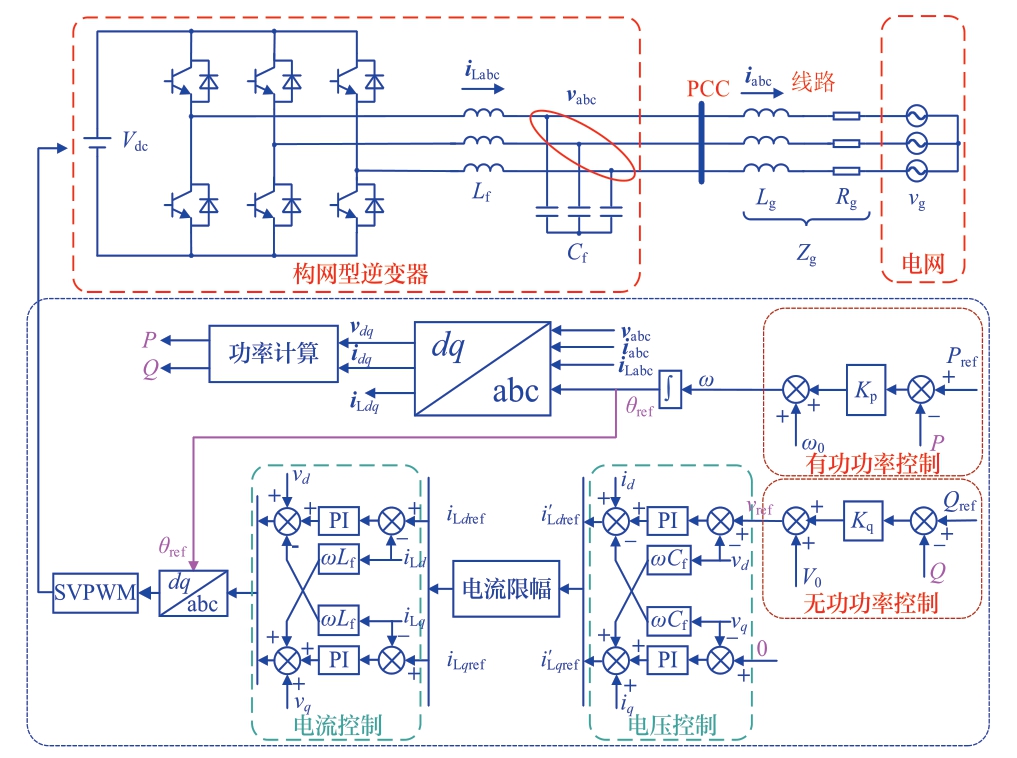
图1 构网型逆变器系统拓扑图及控制框图
Fig.1 System topology and control structure of the GFM inverter

构网型逆变器的控制由外部功率环与内部电压电流环组成。其中外部功率环采用P-f、Q-V下垂控制，Kp和Kq分别为有功功率和无功功率的下垂系数，vref和θref是功率环产生的输出电压的幅值和相位参考，此外θref为控制中dq坐标变换与反变换的参考角度。其中功率环的输出可以表示为

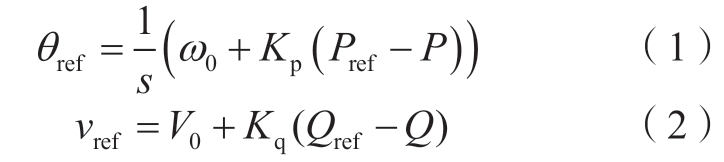
式中：ω0和V0分别为角频率和输出电压参考值；Pref和P分别为有功功率参考和逆变器输出的有功功率；Qref和Q分别为无功功率参考和逆变器输出的无功功率。

构网型逆变器的内部控制环由dq坐标系下的电压电流双环解耦控制组成，为了防止过流损坏逆变器内部的电力电子器件，通常会在电压环与电流环之间增加电流限幅策略。本文采用d轴优先限流器进行限流，在正常模式下，限流器不起作用；而当电网故障使得电感电流参考大于电感电流所允许的最大值Imax时，电流参考直接由限流器给出，其表达式为

式中：iLdref、iLqref为电感电流参考值；、为电压环输出的电感电流参考值。

为了简化后续分析，做出以下假设：①构网型逆变器直流输入侧通常接有大电容或者其他储能设备，因此将其直流侧电压Vdc视为定值；②流过滤波电容Cf中的电流相比于滤波电感Lf中的电感电流太小，可以忽略，近似认为逆变器输出电流等于电感电流；③由于电压环带宽远大于外部功率环，因此在正常模式下，分析由功率环引起的暂态稳定性问题时，可以忽略电压环的动态行为，将逆变器等效成一个电压源；④由于电流环带宽远大于电压环，因此在限流模式下，分析电压环的动态行为时，忽略电流环的影响，考虑电感电流能够快速跟踪其参考[14]。

1.2 模式切换逻辑

在正常模式下，功率环自主产生构网型逆变器输出电压的幅值与相位参考，并经由电压电流环实现电压理想跟踪，其简化电路和电压向量图如图2所示。此时，逆变器的输出功率可以写为

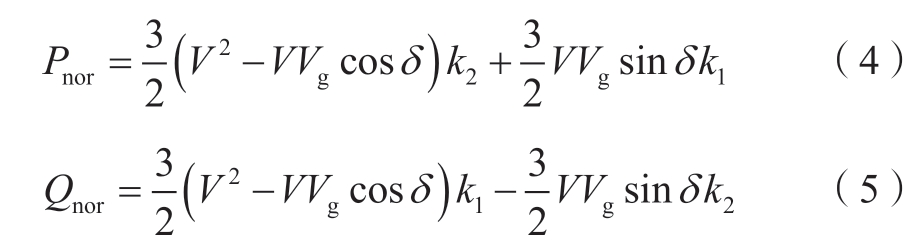
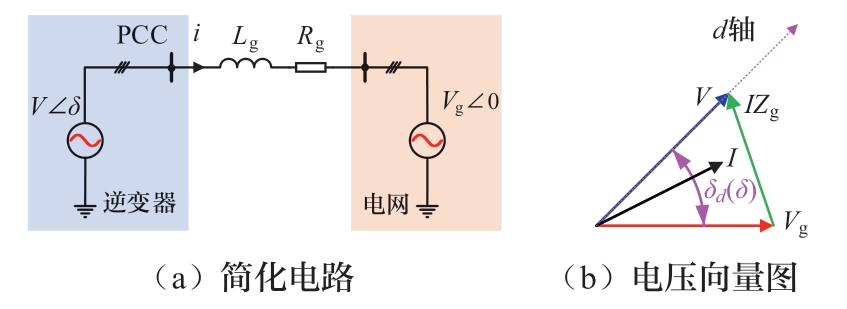
图2 正常模式下构网型逆变器的简化形式
Fig.2 Simplified form of the GFM inverter in the normal mode

式中：V为PCC点的电压幅值，其可以通过联立式（2）和式（5）求得；δ为相角，表现为PCC电压与电网电压的相位差；k1 = Xg/(Xg2+Rg2)；k2 = Rg/(Xg2+Rg2)；δd为d轴与电网电压的相位差，也称为虚拟相角，在正常模式下，V = vref，δd = δ。

根据图2，得到构网型逆变器在正常模式下输出电流的表达式为

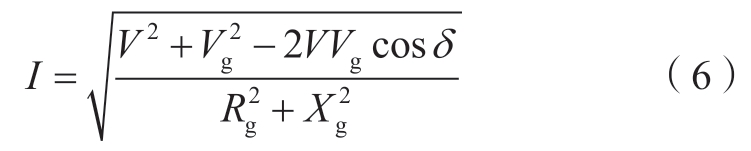
根据式 （3），当电流参考大于Imax时，逆变器进入限流模式。定义此时的功角为模式切换角δs，其表达式由式 （7） 所示。

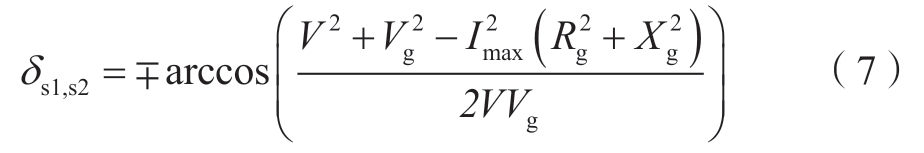
在限流模式下，电感电流参考由限流器给出，构网型逆变器可以等效成一个电流源。图3为限流模式下构网型逆变器的简化电路图，其输出有功功率Plim与PCC电压矢量的表达式分别如下所示：

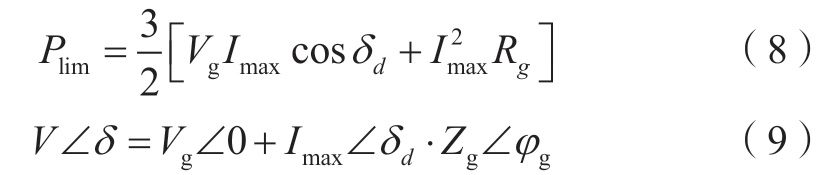
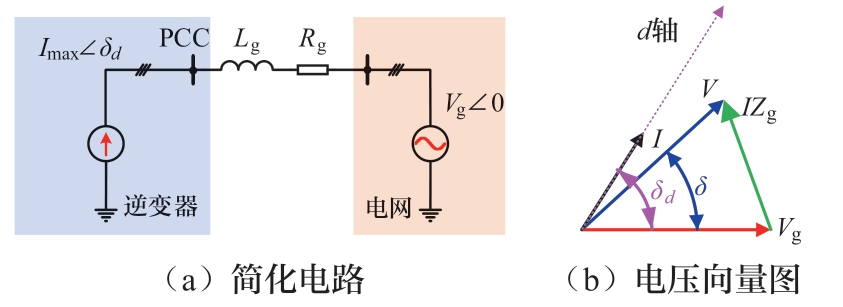
图3 限流模式下构网型逆变器的简化形式
Fig.3 Simplified form of the GFM inverter in current limiting mode

式中：Zg为电网阻抗；φg为电网阻抗角，且

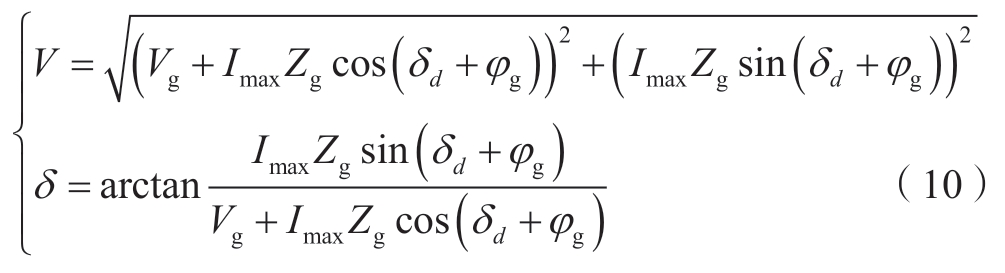
若逆变器能够从限流模式切换回正常工作模式，恢复电压源特性，那么需要让d轴重新以逆变器输出电压定向，且输出电压幅值与正常模式下的电压环参考相等，即

实际上，式（11）包含了幅值与相角2个要求，仅当2个条件同时满足时才能发生从限流模式到正常模式的切换。以Vg = 0.6 pu为例，基于式（10）图4给出了限流模式下的PCC电压及其在正常模式下参考的幅值与相角随虚拟相角的变化曲线，尽管电压幅值曲线存在交点，但相角曲线始终未出现交截情况，说明在整个虚拟相角周期，逆变器无法实现从限流模式到正常模式的自然过渡。

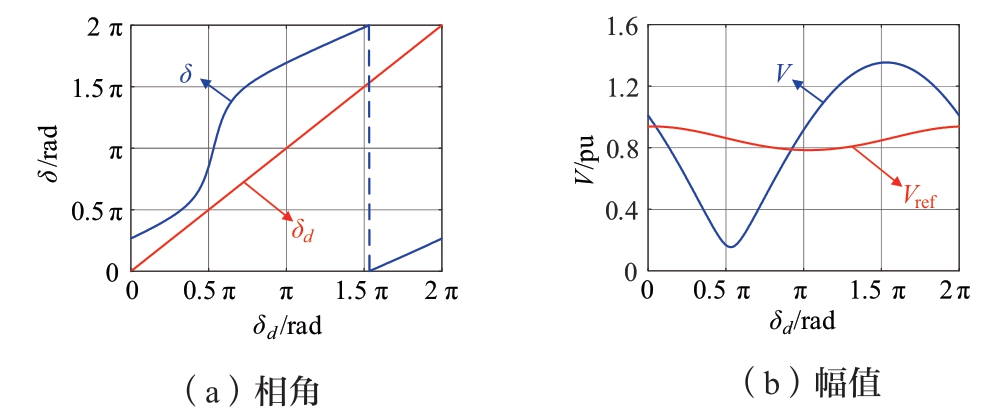
图4 Vg = 0.6 pu时限流模式下的PCC电压及其在正常模式下参考的幅值与相角曲线
Fig.4 The amplitude and phase angle curve of PCC voltage in the current limiting mode and its reference in the normal mode when Vg = 0.6pu

图5显示了不同电网电压下的模式切换角δs1,s2。当构网型逆变器工作在正常模式且δs1 < δ < δs2时，其输出电流小于Imax，因此，该区域称为电流非饱和区。为了阐明构网型逆变器在遭遇不同程度电网故障下的暂态稳定性，图5描绘了由方程Pnor = Pref计算的正常模式下稳定平衡点（stable equilibrium point, SEP）的相位δsep。可以观察到，当电网电压下降时，δs2和δsep都会增大，并且二者曲线在Vg = 0.607 pu处相交。当δs2 < δsep，也即Vg < 0.607 pu时，构网型逆变器在故障后到达正常模式下的SEP之前将不可避免地进入限流模式，且此后在自然状态下无法实现向正常模式的过渡，这表明逆变器无法在正常模式下保持稳定。

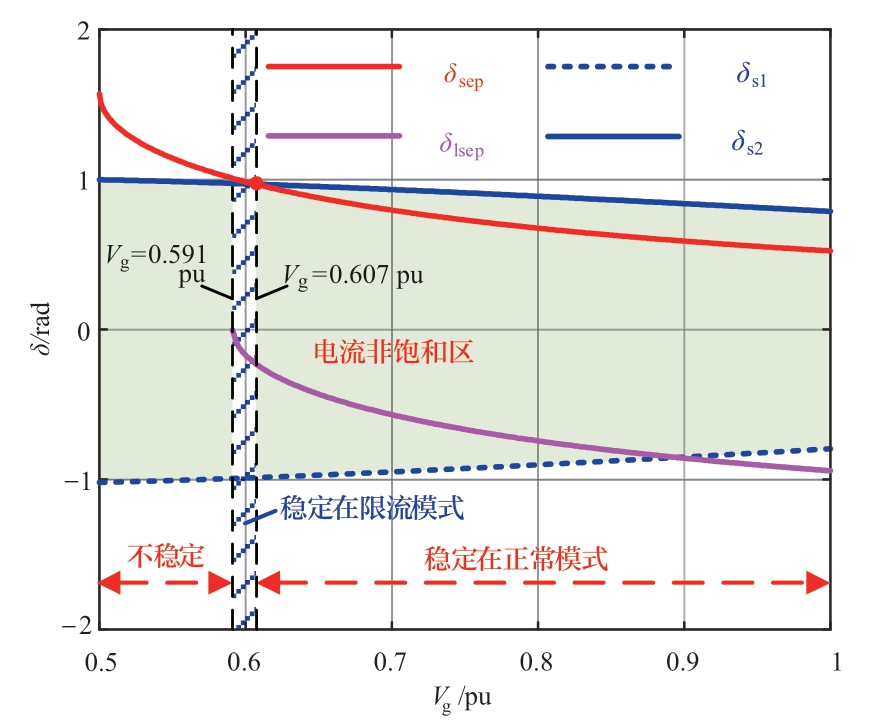
图5 不同电网电压下的模式切换角δs与新稳定点的相位δsep，δlsep
Fig.5 Mode switching angle δs and phase δsep, δlsep of new SEP under different grid voltages

此外，为了区分进入限流模式后的稳定性，图5还描绘了由方程Plim = Pref计算的限流模式下SEP的相位δlsep随电网电压Vg变化的曲线。如图所示，当电网电压Vg进一步降至0.591 pu以下时，限流模式下的P-δ曲线与参考功率没有交点，其最大输出有功功率小于功率参考值，构网型逆变器将无法与电网保持同步，导致暂态不稳定。仅当0.591 pu < Vg < 0.607 pu时，逆变器会进入限流模式，并最终稳定在限流模式，但此时逆变器处于电流源状态，其输出电压不可控，且减速面积小，稳定裕度低，无法对电网电压起支撑作用。

2 电流抗饱和策略

构网型逆变器触发限流的条件是电压环产生的电流参考值大于限流值Imax，而一旦进入限流模式，在自然状态下很难恢复到正常模式。因此，有必要设计电流抗饱和控制，以保证构网型逆变器的正常非饱和运行。

电压环的控制示意图如图6所示，其控制的目标是使逆变器的输出电压vdq跟踪其参考vrefdq。首先将电压vdq与其参考vrefdq的误差信号送入PI控制器进行调节，同时引入解耦控制回路，因此电压环的输出i'Lref由两部分组成：实际电感电流（忽略电容器动态时，iLdq =idq+jωCfvdq）和电压PI控制器的输出，其等效电压控制图如图7所示。在限流模式下，电感电流参考由限流器给出，实际电感电流等于限流幅值Imax。

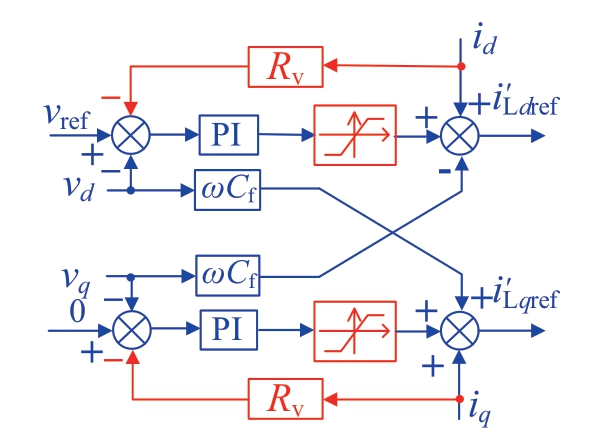
图6 构网型逆变器电压控制框图
Fig.6 Voltage control block diagram of the GFM inverter

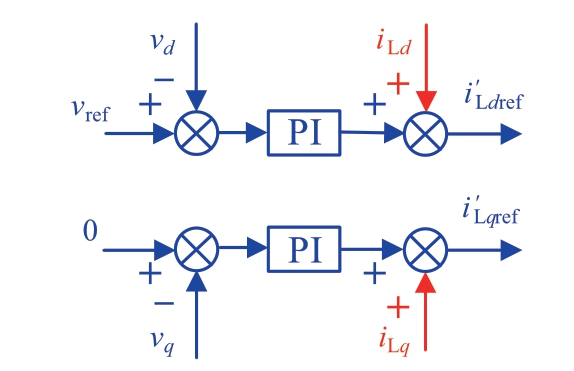
图7 构网型逆变器电压控制等效图
Fig.7 Equivalent diagram of voltage control for the GFM inverter

同样以Vg = 0.6 pu为例，图8为限流模式下的PCC电压及其参考的dq分量随虚拟相角δd的变化曲线。对d轴分量，电压参考vref总是大于PCC电压vd，PI控制器的输出持续增加，这进一步阻止了构网型逆变器回到正常模式。因此在实际控制中对PI控制器进行限幅，将其输出限制在[-Ilim，Ilim]内，其示意图如图6红线所示。此外，由于在限流模式下电压环失效，引入虚拟电阻Rv不会改变逆变器的动态特性，但它显著降低了d轴参考电压vref。随着虚拟电阻的增加，vd与vref曲线发生交截，当vd > vref时，d轴PI控制器的输出将在一段时间后从Ilim变为-Ilim。限流模式下，电流严格d轴定向，iLd = Imax，iLq = iq = 0，因此Rv对电压的q轴分量没有影响，q轴PI控制器的输出也为-Ilim。若需要逆变器脱离限流模式，则须满足

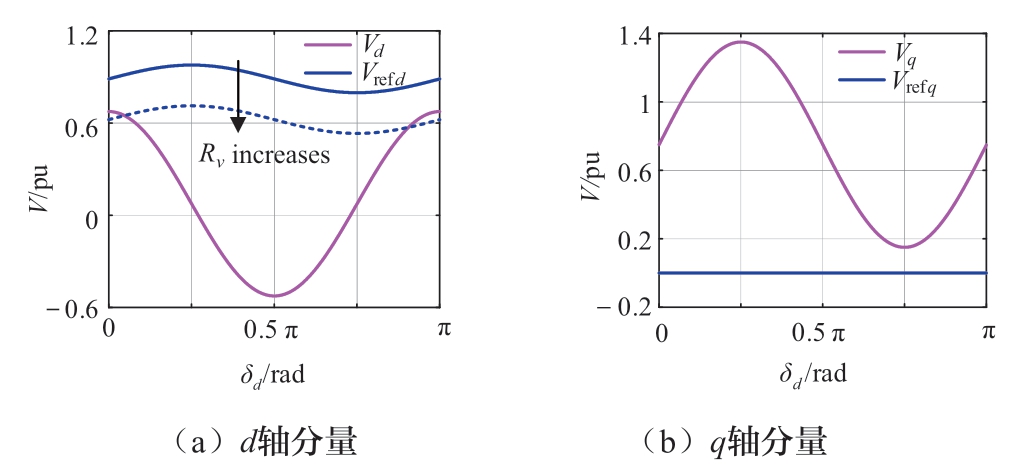
图8 限流模式下的PCC电压及其参考
Fig.8 PCC voltage and its reference in the current limiting mode

综上所述，在电流抗饱和策略中，虚拟电阻Rv的设计需要确保vd与vref存在交点，PI控制器限幅值设计条件为Ilim < Imax。一旦i'Lref < Imax且虚拟相角δd在电流非饱和区[δs1，δs2]内，构网型逆变器将退出限流模式。

3 仿真验证

为了验证对构网型逆变器暂态稳定性分析和所提控制策略的有效性，在MATLAB/Simulink平台中进行了仿真验证，其系统与控制参数如表1所示。在电网故障发生前，构网型逆变器都处于正常模式，且电网电压幅值Vg = 1.0 pu，电网故障均发生在t = 1 s处。

表1 系统与控制参数
Table 1 System and control parameters

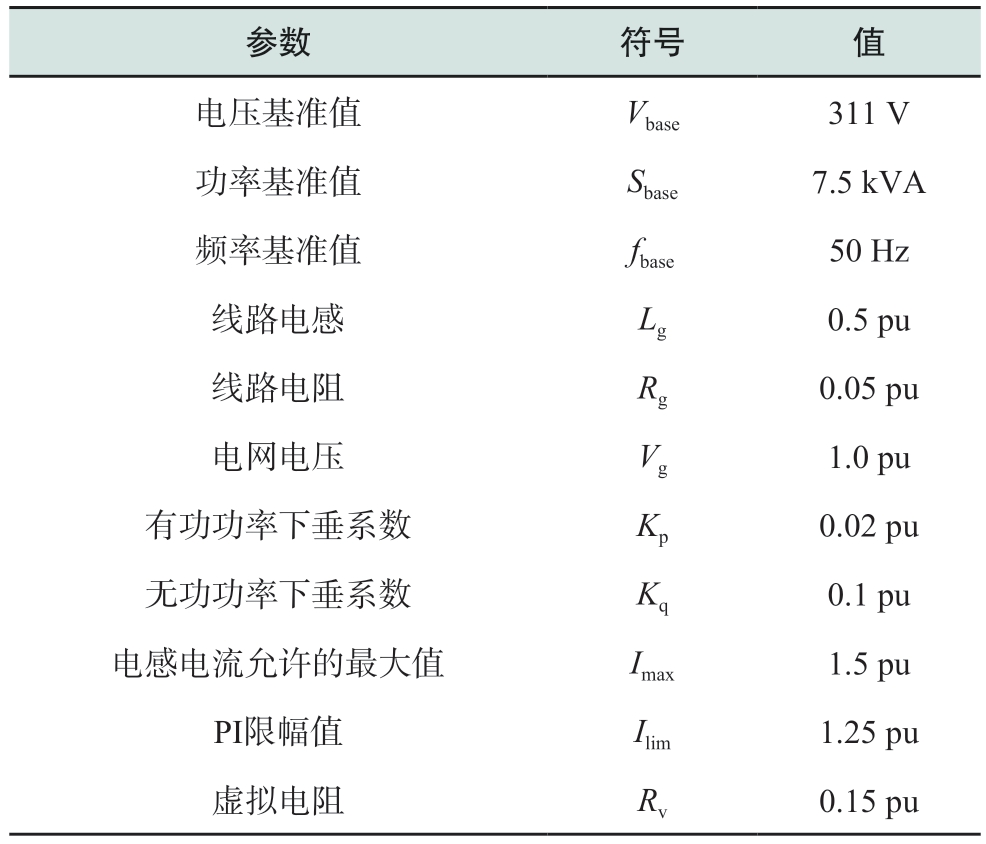
参数 符号 值电压基准值 Vbase 311 V功率基准值 Sbase 7.5 kVA频率基准值 fbase 50 Hz线路电感 Lg 0.5 pu线路电阻 Rg 0.05 pu电网电压 Vg 1.0 pu有功功率下垂系数 Kp 0.02 pu无功功率下垂系数 Kq 0.1 pu电感电流允许的最大值 Imax 1.5 pu PI限幅值 Ilim 1.25 pu虚拟电阻 Rv 0.15 pu

3.1 冲击电流与暂态虚拟电阻

图9 （a） 为Vg = 0.6 pu时没有限流保护的构网逆变器遭遇电网故障时的仿真波形图，除了前文提到的稳态过流，逆变器在故障发生瞬间也存在瞬态过流风险。而在d轴优先限流器作用下，图9 （b） 中构网型逆变器在故障发生后就始终处于限流模式。文献[26]中提到使用瞬态虚拟电阻可以抑制逆变器的瞬态过流现象，且其对暂态稳定性的影响可以忽略不计，因此在后续分析中，在故障瞬间都对逆变器采用瞬态虚拟电阻以防止出现瞬态过流现象。

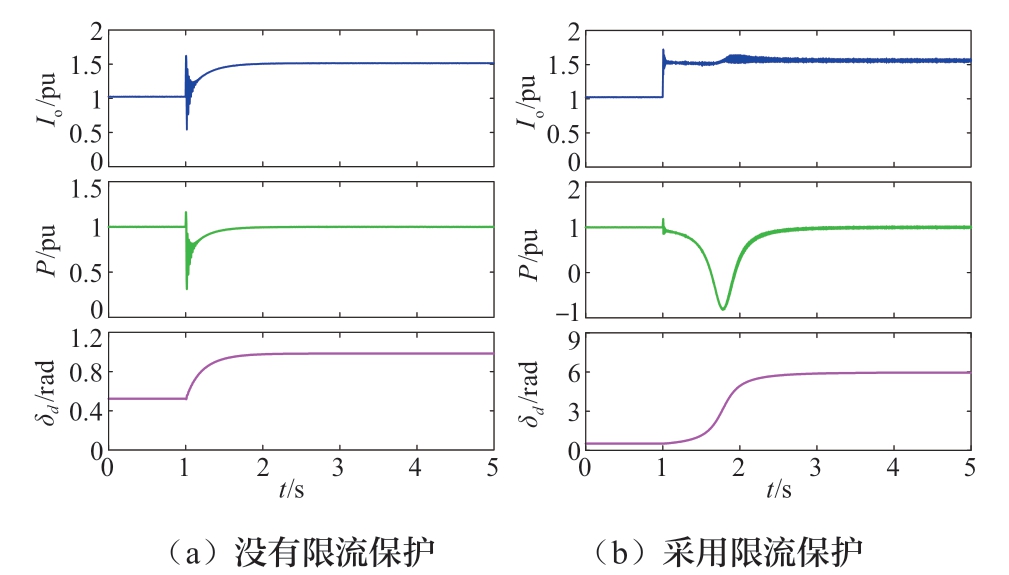
图9 限流保护对暂态稳定性的影响
Fig.9 Influence of current limiting protection on transient stability

3.2 不同电网压降下的暂态稳定性

图10为构网型逆变器采取暂态虚拟电阻后在不同电网压降下的仿真波形图。当Vg = 0.8 pu时，逆变器始终保持在正常模式且最后恢复稳定；当Vg = 0.4 pu时，逆变器在相角超过模式切换角后进入并一直保持在限流模式，且由于最大输出功率小于参考功率而发生暂态失稳，无法与电网保持同步；仅当Vg = 0.6 pu时逆变器在进入限流模式后，最终稳定在了限流模式的SEP上。

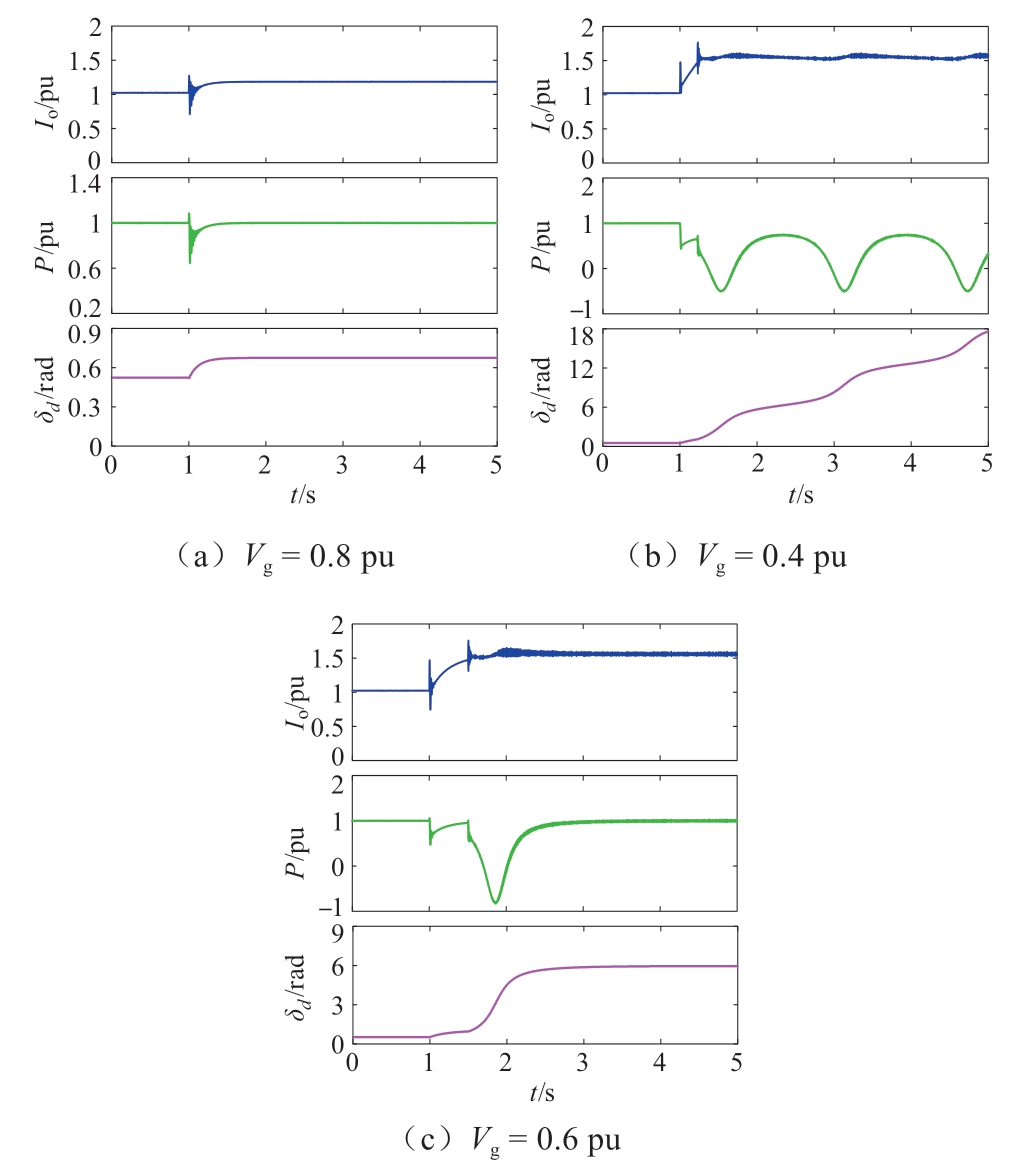
图10 构网型逆变器在不同电网压降下的仿真波形图
Fig.10 Simulation waveforms of the GFM inverter under different grid voltage sags

3.3 所提电流抗饱和策略的有效性

为了验证所提电流抗饱和策略的有效性，在图10（c）的基础上在t = 3s时加入引入PI限幅与虚拟电阻，其仿真波形图如图11所示。在控制策略生效后经过一段时间系统恢复到了正常模式，其输出电流明显降低，这段时间为d轴PI控制器的退饱和过程，其输出从Ilim变为-Ilim。但由于电网故障并未得到清除，逆变器相角仍不断增大，在相角超过模式切换角后再一次进入限流模式，并重复之前的暂态行为。

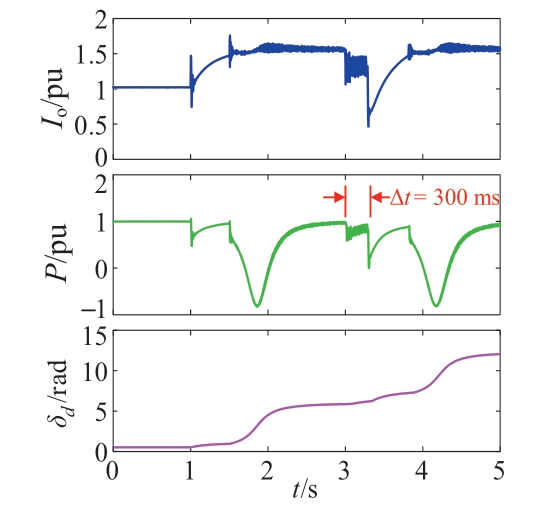
图11 Vg = 0.6 pu时采取电流抗饱和策略下的仿真波形图
Fig.11 Simulation waveform with current anti saturation strategy when Vg = 0.6 pu

为了探究PI限幅值Ilim与虚拟电阻Rv的大小对电流抗饱和的作用效果，图12分别为仅采用PI限幅、仅采用虚拟电阻、PI限幅值为1 pu和虚拟电阻为0.25 pu时的仿真波形图。从图12 （a） 和 （b） 中可以看出，仅使用电流抗饱和策略中的单一策略无法使逆变器恢复正常模式，而图12 （c） 和（d） 说明减小PI限幅值或增大虚拟电阻的大小可以加快构网型逆变器模式切换的速度。

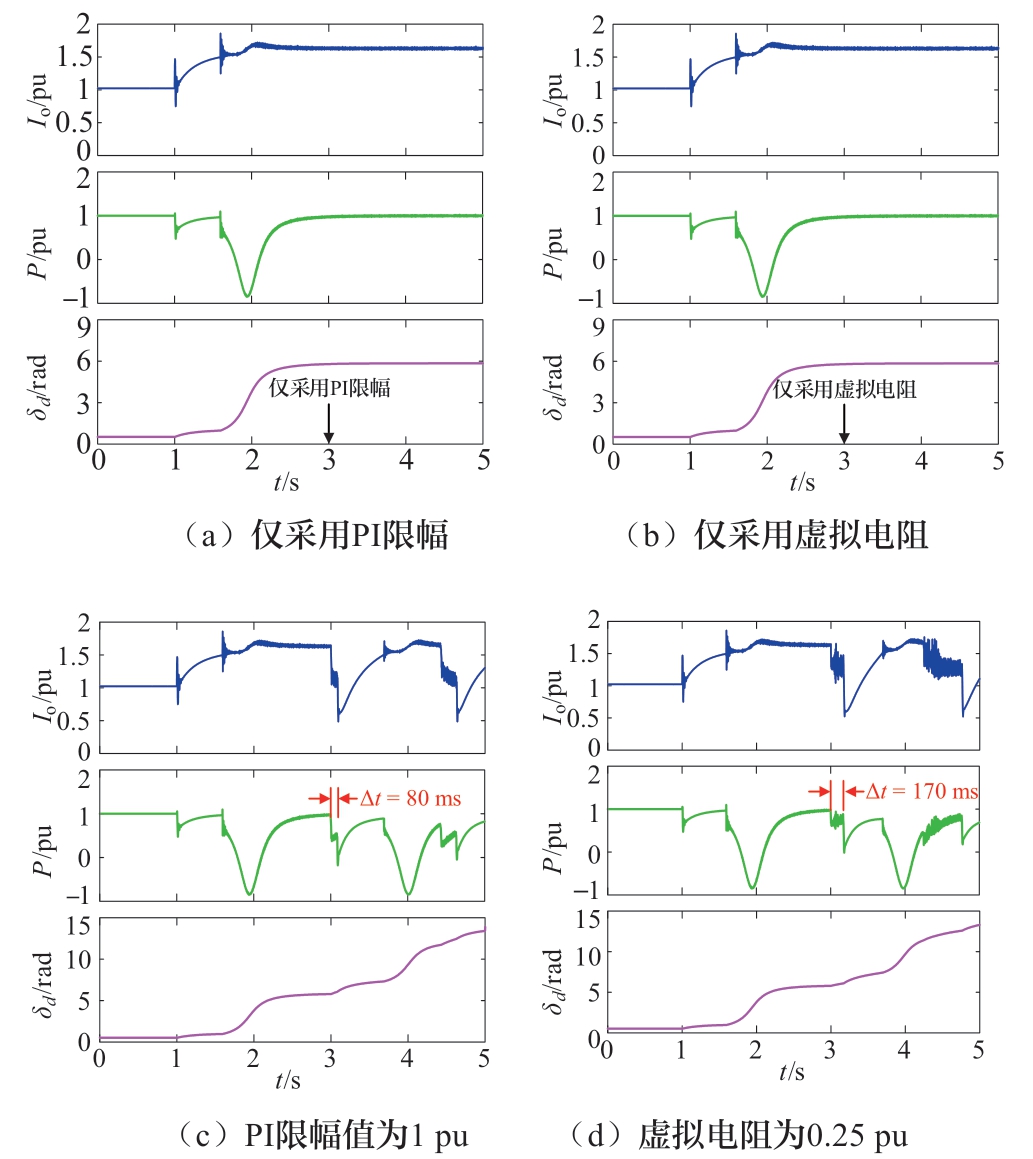
图12 Vg = 0.6 pu时的仿真波形图
Fig.12 Simulation waveform when Vg = 0.6 pu

图13为复杂电网故障条件下的仿真波形图，其中在t = 1 s时Vg跌落至0.6 pu，在t = 3 s时Vg恢复至0.8 pu，唯一不同的是图13 （b） 在电网故障恢复瞬间采用所提控制策略。在不采取任何控制策略情况下，图13 （a）在故障部分恢复后仍然处于限流模式，仅有相角略微减小；而图13 （b） 在故障部分清除后恢复正常模式且保持稳定。

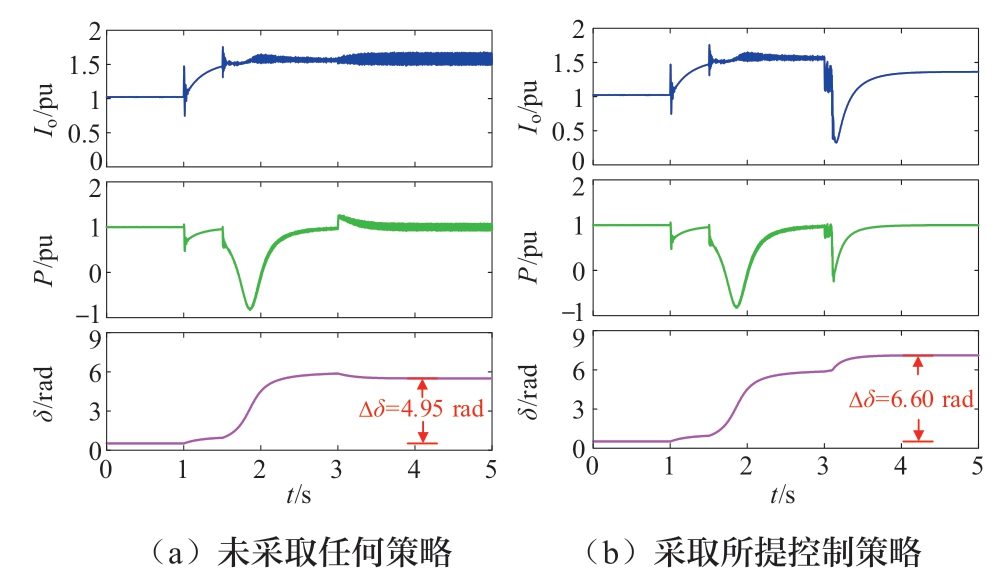
图13 电网故障且部分恢复后的仿真波形图
Fig.13 Simulation waveforms after fault and partial recovery

除电压跌落外，相位跳变也是电网常见故障之一。图14给出了电网相位跳变后的仿真波形图，其中在t = 1s时发生电网相位跳变Δθg = -0.5 rad，图14（a）在故障后并未采取任何策略，逆变器在经过一段时间后一直处于限流模式；图14（b）在故障后采取了所提控制策略，逆变器在同样经过一段时间后恢复到了正常模式，但由于电流抗饱和策略中虚拟电阻的存在，逆变器的稳态输出电流大于1 pu，因此在t = 3 s时撤去了所提控制策略，逆变器最终恢复到了故障前的稳态工作点。仿真结果与前文理论分析一致，验证了理论分析的正确性与所提控制策略的有效性。

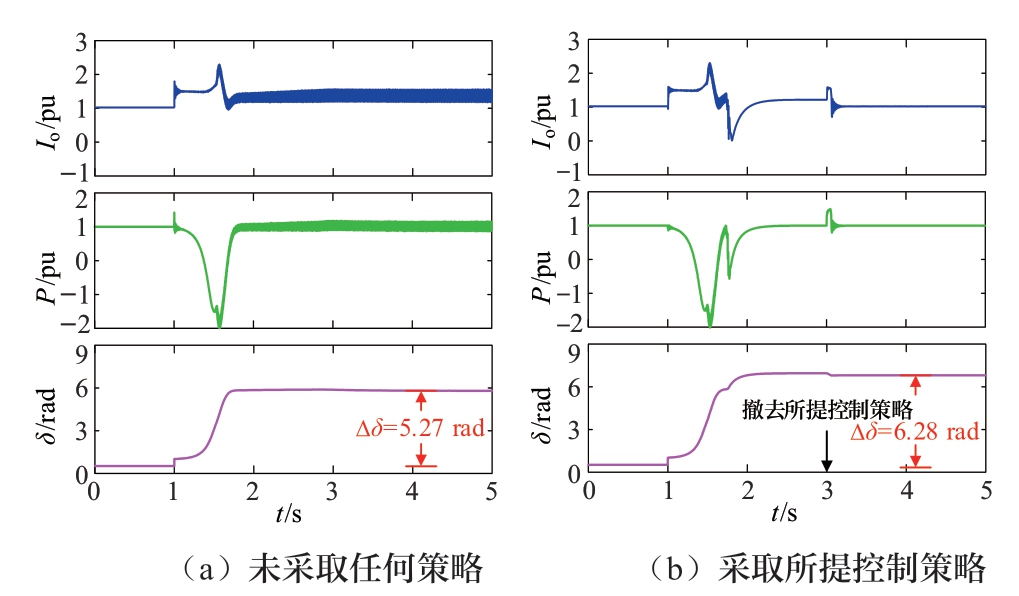
图14 电网相位跳变后的仿真波形图
Fig.14 Simulation waveforms after phase jump of the grid

4 结论

本文研究了构网型逆变器在限流保护下的暂态稳定现象，在考虑无功控制环的基础上，通过模式切换角与新稳定点的相位大小关系描述了构网型逆变器在不同电网故障下的动态行为，刻画了不同模态的运行边界，推导了构网型逆变器的模式切换条件。针对构网型逆变器难以从限流模式过渡到正常模式的现象，提出了一种基于虚拟电阻和PI控制器限幅的电流抗饱和策略，并给出了PI控制器限幅值的设计范围。仿真结果表明，本文提出的电流抗饱和策略不仅能抑制故障过程中的积分器饱和现象，还能促进构网型逆变器从限流模式恢复到正常电压源模式，增强了故障清除后构网型逆变器的暂态稳定性与构网能力。