相关论文:
-

-
全球能源互联网
第8卷 第6期 2025年11月;页码:677-689
同步机电源占比对经柔性直流送出的新能源基地电网暂态同步稳定性的影响
Influence of Proportion of Synchronous Generator on Transient Synchronous Stability of Renewable Energy Base Grid Transmitted by VSC-HVDC System
- 浙江大学电气工程学院,浙江省 杭州市 310027
- FANG Jie, ZHANG Zheren*, XU Zheng (College of Electrical Engineering, Zhejiang University, Hangzhou 310027, Zhejiang Province, China
关键词
Keywords
摘 要
Abstract
新能源联合水电等同步机电源经柔性直流送出的外送模式具有传输高效、调控灵活以及供能可靠等优势,能够提升能源利用率、促进能源结构的优化转型。采用V/f控制的送端换流站能够良好应用于纯新能源送出场景,但在新能源联合同步机电源外送的场景下,二者的容量占比将影响送端交流系统的暂态稳定性。为探讨同步机电源占比对该送端系统暂态稳定性的影响,首先构建了送端交流系统暂态稳定性分析通用模型,随后阐述了基于能量型Lyapunov函数的暂态稳定性分析方法,分析了同步机电源占比对Lyapunov暂态稳定边界以及暂态过程的影响,研究了满足暂态稳定性要求的同步机电源容量占比,最后通过仿真验证了理论分析的准确性和有效性。
The hybrid transmission mode of renewable energy combined with hydropower and other synchronous generators transmitted by voltage source converter high-voltage direct current (VSC-HVDC) offers high-efficiency transmission,flexible regulation and reliable power supply.It enhances the efficiency of energy utilization and promotes the optimization and transformation of energy structures.The adoption of Voltage-to-Frequency (V/f) control strategy in the sendingend converter station can be effectively applied to the power transmission of pure renewable energy base.However, in the scenario where renewable energy is integrated with synchronous generator power for external transmission, the capacity proportion between the two will affect the transient stability of the sending-end AC system.To investigate the impact of synchronous generator capacity proportion on the transient stability of this sending-end system, a generalized analytical model for transient stability assessment in sending-end systems is established firstly.Subsequently, an analysis method for transient stability based on Lyapunov energy function is proposed to analyze how the capacity proportion influences the boundary of Lyapunov transient stability and the transient process.Furthermore, the critical capacity proportion of synchronous generator that meets the requirements of transient stability is studied.Finally, the accuracy and effectiveness of the theoretical analysis are verified through simulation.
0 引言
作为能源转型进程中的关键任务,构建新型电力系统能保障能源的安全可靠供应,实现能源领域的绿色发展[1-6]。以中国西部地区为主的九大清洁能源基地具有新能源储备优势,未来将有力推动新型电力系统的构建[7-9]。2023年底,西部地区12个省份新能源装机总规模已超4亿kW[10],以光伏、风电为代表的新能源凭借其清洁、可再生的显著优势在电力供应体系中的地位日益提升[11-16]。水电、火电等同步机电源因其技术成熟等优势,在能源转型进程中也起着重要作用[17-21]。为提高能源调度灵活性与新能源消纳水平,西部地区正依托新能源与水电的互补特性实现水风光一体化规划建设,布局了金沙江、澜沧江上游等水风光一体化基地,其中,雅砻江流域水风光一体化基地的累计发电量已突破1万亿kWh,成为世界最大的清洁能源基地[8,22]。
然而,中国能源资源与负荷中心呈逆向分布[23],能源在生产和消费上的平衡需要通过大规模跨区域输电工程来实现。在大规模新能源基地外送场景中,基于模块化多电平换流器的柔性直流输电系统(modular multilevel converter based high voltage direct current,MMC-HVDC)能为远距离电力传输提供更高效、灵活且稳定的解决方案[24-28]。对新能源联合同步机电源经柔性直流(voltage source converter high-voltage direct current,VSC-HVDC)外送模式而言,送端系统涉及的多类型设备间具有复杂的动态耦合机理,目前已有学者针对该场景开展了控制策略、小信号稳定性、调度优化等方面的研究。文献[29]考虑送端双换流站协同配合与大基地-多端柔直系统功率传递过程,提出了一种支撑受端频率的水光互补新能源基地-多端柔性直流输电系统协同控制策略及参数优化方法。文献[30]针对风光火打捆外送系统并网产生的低频振荡问题,提出了一种抑制低频振荡的控制器优化策略。文献[31]综合考虑了稳态电气参数和小信号稳定性,定量评估了全跟网型光伏场景下水光不同出力配比时柔直的功率传输范围。文献[32]聚焦水风光互补系统,探讨了长期、短期尺度下的多能源互补协调运行问题。
清洁能源基地中的电源容量占比是系统规划设计阶段需要重点关注的问题,其关乎电力系统的整体效能与可持续发展。文献[33]聚焦新能源基地交流送出场景,推导了跟网型新能源场站所需的构网型变流器容量配比,以保障新能源场站的安全稳定运行。文献[34]构建了风-光-氢综合能源系统容量配置优化及决策模型,以应对新能源出力与电负荷的不确定性,并响应未来电动汽车的充电需求。文献[35]针对新能源基地接入弱电网场景中的构网型变流器定容问题,从小干扰稳定视角提出了构网型与跟网型变流器容量配比的解析公式和估算方法。在纯新能源送出场景下,采用V/f控制的送端换流站能够为送端系统提供稳定的电压幅值及频率支撑[36],V/f控制策略目前已被证明有良好应用[37]。然而,在新能源联合同步机电源送出的场景下,不合理的同步机电源占比将威胁系统的安全稳定运行[31],甚至可能造成电源与送端换流站发生失步,此时V/f控制策略可能不再适用于送端换流站,但文献[33-35]等对容量配置的研究并未从暂态稳定性的角度对常规控制策略在上述送出场景下的适应性进行评估,因此分析同步机电源占比对上述送端系统暂态稳定性的影响仍具有重要研究价值。同时,尽管Lyapunov法在电力系统暂态稳定性分析中已有运用[38-41],但利用能量型Lyapunov函数对此展开分析仍具有较大应用潜力。
本文针对新能源联合同步机电源经柔直送出的送端交流系统建立暂态稳定性分析数学模型,运用能量型Lyapunov函数法剖析同步机电源容量占比对送端系统暂态稳定性的影响,并基于此提出容量占比的评估方法,最终通过时域仿真软件PSCAD验证理论分析的正确性与所提方法的有效性。
1 经柔直送出的新能源-同步机电源送端系统简介
本文以图1所示的新能源联合同步机电源经柔性直流送出系统的送端交流系统为研究对象。其中,新能源基地、同步机电源分别经交流线路1、交流线路2连接至送端换流站交流母线PCC1处。
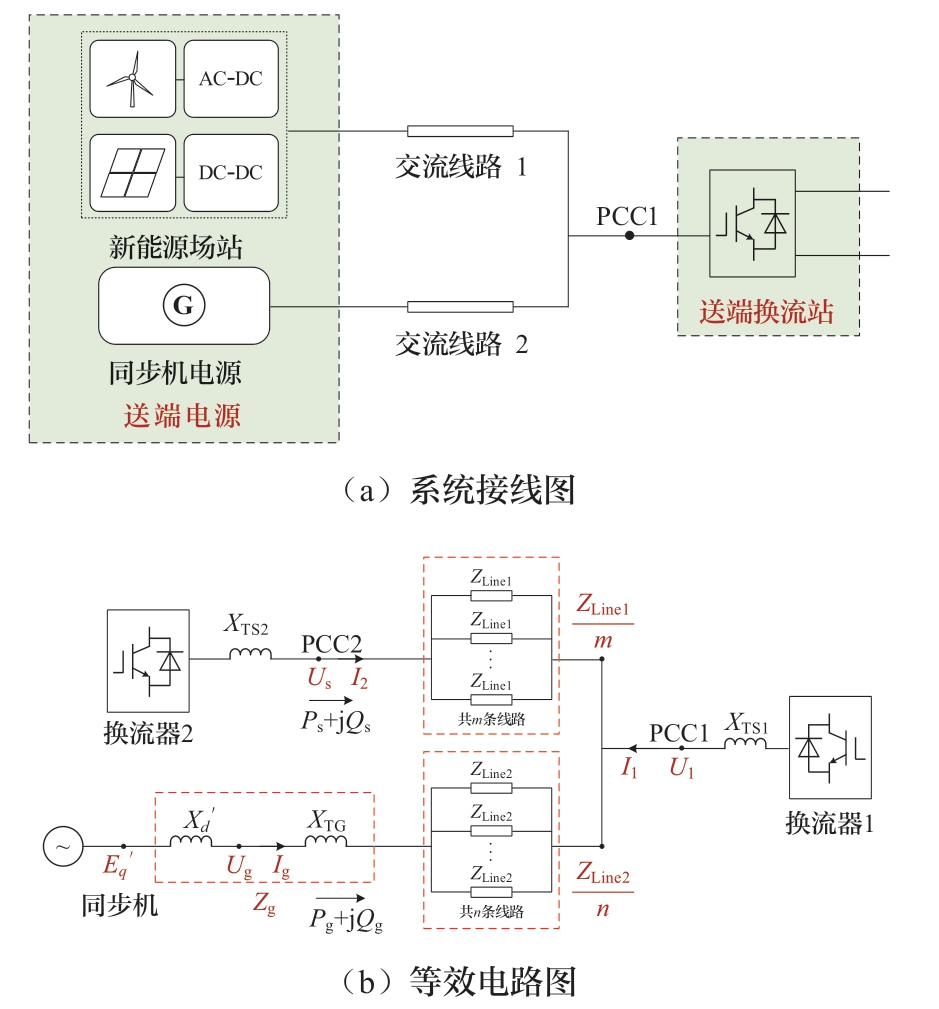
图1 新能源联合同步机电源经柔直送出的送端系统
Fig.1 Sending-end system with renewable energy-synchronous machine transmitted by VSC-HVDC
针对所研究的暂态稳定性问题,本文采用的前提和假设如下。
1)送端换流站采用V/f控制模式。送端换流站为整个新能源基地电网确立支撑电源,即送端换流站确立整个新能源基地电网的运行频率,同时控制送端换流站交流母线PCC1点电压幅值恒定。
2)送端新能源基地电网的暂态稳定性主要表现在送端新能源基地3个电源(即送端换流站、新能源基地的非同步机电源和同步机电源)之间的同步稳定性。由于送端换流站确立了送端新能源基地电网的额定频率运行条件,送端新能源基地3个电源之间的同步稳定性就表现为新能源基地的非同步机电源保持额定频率运行的能力以及同步机电源保持额定频率运行的能力。因此本文在暂态稳定性分析中,主要考察新能源基地的非同步机电源和同步机电源在大扰动下回到额定频率运行的能力。
3)送端换流站的直流电压由其他换流站控制,在研究中忽略送端换流站直流电压的动态变化,即假设送端换流站直流侧为理想直流电压源。
4)柔直与新能源并网换流器的内环电流控制器响应速度较快[42-43],在暂态稳定性的研究过程中不考虑电流内环的动态特性。
5)理论推导时,同步机采用经典二阶模型,暂态过程中保持E'q不变。
6)高压交流输电线路、变压器及同步机等效阻抗中的电阻分量相对较小,因此忽略其影响。
经过上述简化,图1 (a)所示的送端系统可等效为图1 (b) 所示的电路,其中代表送端换流站的换流器1采用V/f控制,代表新能源场站的换流器2采用当前广泛应用于新能源并网的跟网型控制。图1 (b) 中,ZLine1、ZLine2分别为线路1 (共m回)、线路2(共n回)中每回输电线路的阻抗。XTS1、XTS2、XTG分别为换流器1的联接电抗、换流器2的联接电抗、同步机升压变压器的漏抗。![]() 为同步机的暂态电抗;Zg为
为同步机的暂态电抗;Zg为![]() 与XTG的阻抗之和。U1和I1分别为PCC1处的电压和注入电流;Us、I2、Ps和Qs分别为换流器点PCC2处的电压、注入电流、输出有功功率与输出无功功率;
与XTG的阻抗之和。U1和I1分别为PCC1处的电压和注入电流;Us、I2、Ps和Qs分别为换流器点PCC2处的电压、注入电流、输出有功功率与输出无功功率;![]() 为同步机的q轴暂态电势,Ig、Pg和Qg分别为同步机的机端注入电流、输出有功功率与输出无功功率。
为同步机的q轴暂态电势,Ig、Pg和Qg分别为同步机的机端注入电流、输出有功功率与输出无功功率。
2 暂态稳定分析通用模型
2.1 通用性等值电路建模
在本文中,Adq、Adsqs、Adgqg分别为相量A在换流器1的dq旋转坐标系、换流器2的dsqs旋转坐标系、同步机的dgqg旋转坐标系中的矢量表示。其中:δ、δPLL分别为dg轴(对应E′q)、ds轴与d轴之间的夹角,ω、ωPLL分别为其角速度。
同步机和换流器的三相接地故障通常比单相接地故障更为严重[44],因此本文后续仅针对交流系统中某一回送出线路发生更为严重的三相金属性接地故障进行推导,并将换流器2送出线路、同步机送出线路发生故障分别记为故障1、故障2。根据图1所示拓扑,本文将考虑故障态和非故障态的等值电路归纳为图2所示的通用性电路。
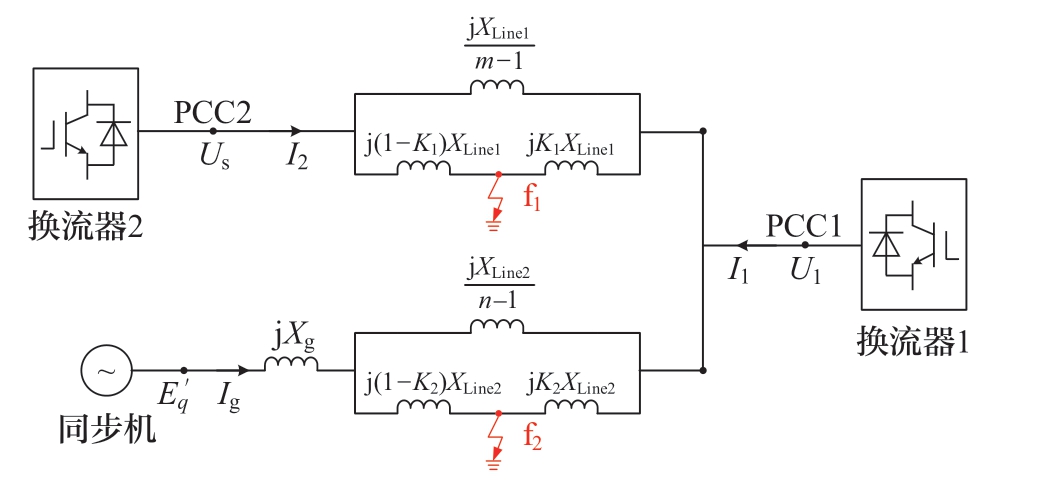
图2 送端系统通用性等值电路图
Fig.2 Generalized equivalent circuit model of the sending-end system
其中:XLine1、XLine2分别表示线路1、线路2中每回输电线路的阻抗;Ki用于描述故障i的发生位置fi,当Ki越接近于0时,线路i上的故障点fi离换流器1越近,i=1或2,且满足Ki∈(0,1)。
非故障态下,换流器1、换流器2的外特性分别等效为电压源、电流源;故障态下,换流器1、换流器2的外特性均等效为电流源[36]。令I1max、I2max分别表示限流状态下换流器1和换流器2的输出电流相量,φ1、φ2分别为I1max与d轴、I2max与ds轴之间的夹角。根据图2所示等值电路推导可知,故障态下同步机的机端电流Ig、换流器2的PCC电压Us均与I1max、I2max、E′q耦合,由此得到故障态下Ig与Us的表达式为
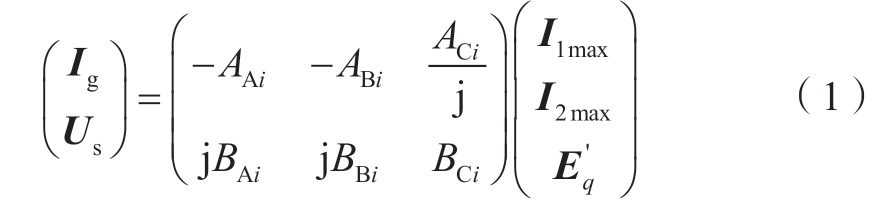
式中:Ig、Us、I1max、I2max、![]() 为上文提及电气量的相量形式,pu;AAi、ABi、ACi、BAi、BBi、BCi为影响因子(i=1或2,对应于故障i的发生),均为非负常数,表征了I1max、I2max与
为上文提及电气量的相量形式,pu;AAi、ABi、ACi、BAi、BBi、BCi为影响因子(i=1或2,对应于故障i的发生),均为非负常数,表征了I1max、I2max与![]() 对Ig或Us的影响程度,其表达式与故障位置、系统阻抗参数等有关,具体见附录A式(A1)—(A12)。
对Ig或Us的影响程度,其表达式与故障位置、系统阻抗参数等有关,具体见附录A式(A1)—(A12)。
2.2 跟网型换流器的暂态稳定性分析模型
换流器1采用V/f控制且忽略其内环电流控制的影响,因此其不存在失步问题,本文仅考虑换流器2与同步机的暂态过程。对于暂态稳定性分析,如果只考虑锁相环动态,换流器2的并网动力学模型与同步机类似[45-46]:
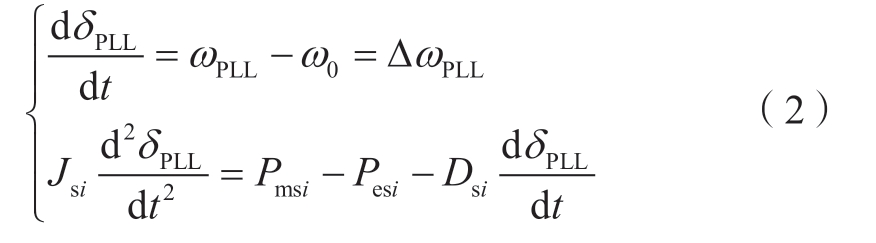
式中:Jsi为换流器2等效惯性系数(i=0表示系统处于非故障态,i=1或2表示故障发生于线路i上);Pmsi为换流器2等效机械功率,pu;Pesi为换流器2等效电磁功率,pu;Dsi为换流器2等效阻尼系数。
2.3 同步机的暂态稳定性分析模型
同步机的二阶转子运动方程表达式为
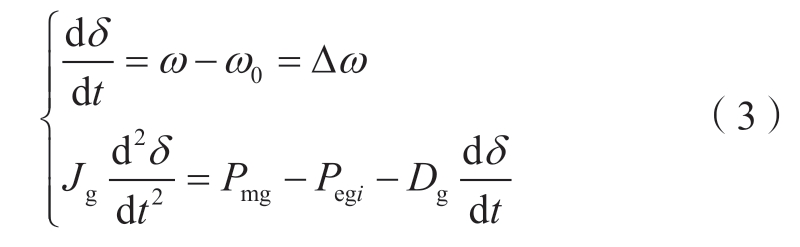
式中:Jg为同步机惯性系数;Pmg为同步机机械功率,pu;Pegi为同步机电磁功率(i=0表示系统处于非故障态,i=1或2表示故障发生于线路i上),pu;Dg为同步机阻尼系数。
暂态过程中,除Pegi外的上述其余量均可视为常数,因此需着重关注Pegi在2种状态下的表达式。
非故障态下,Peg0的表达式为
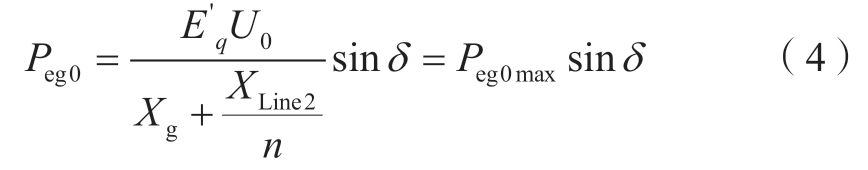
故障下的Ig转换至dgqg旋转坐标系后,记为
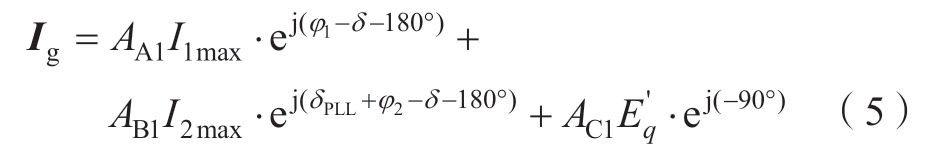
由此得到故障态下的Pegi表达式为
其中:
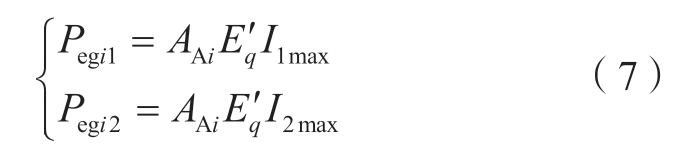
2.4 描述故障下送端系统暂态稳定性的状态方程
根据式(2)—(7),用于上述送端系统暂态稳定性分析的状态方程推导结果为

式中:Ai为状态方程系数(i=1,2,…,11),均为非负常数,其表达式见附录A式(A13)—(A23)。
附录 A 各影响因子与状态方程系数的详细表达式
2.1节中各影响因子AAi,ABi,ACi,BAi,BBi,BCi(i = 1 或 2)的详细表达式如式(A1)—(A12)所示。


2.4节中各状态方程系数Aj( j=1,2,…,11)的详细表达式如式(A13)—(A23)所示。
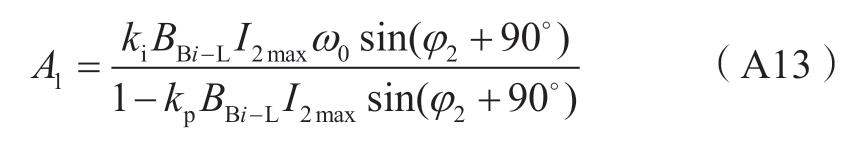

其中:
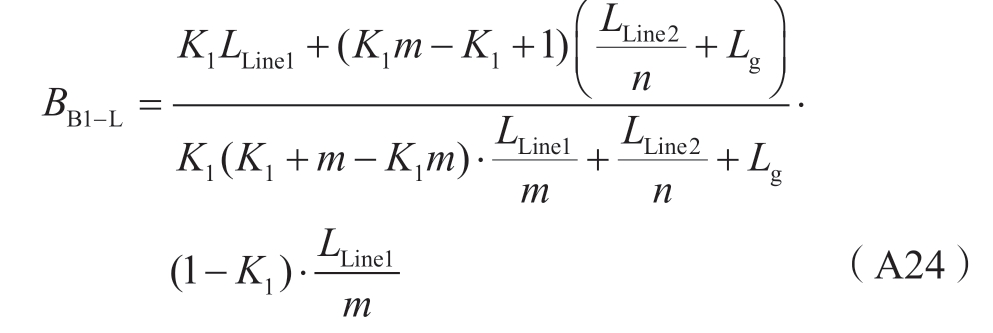
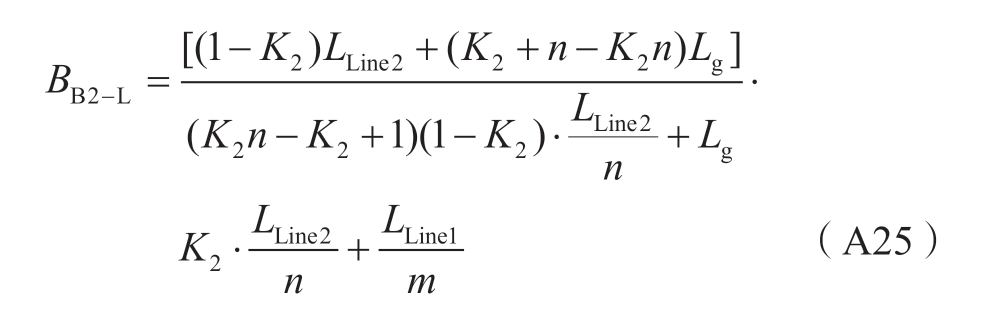
3 基于能量型Lyapunov函数的送端交流系统暂态稳定性评估方法
3.1 送端交流系统的能量函数构建
经过合理的控制设计与参数优化后,换流器2的同步单元PLL可具备良好的锁相能力,使其暂态稳定性明显优于同步机[47-49]。因此,本文评估送端交流系统暂态稳定性时着重关注同步机的暂态稳定性。
根据图2所示,不考虑阻尼项时,同步机在稳态运行下的转子运动方程为
现以如下2个平衡点为积分初始点δEP与ΔωEP:
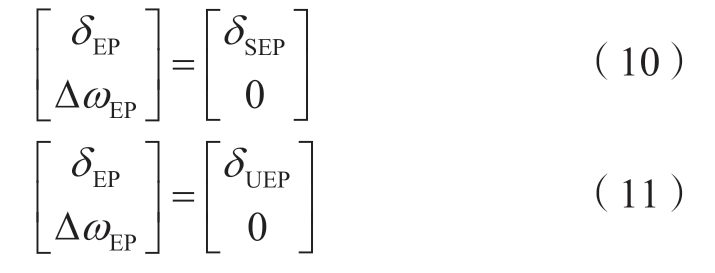
式中:δSEP为同步机稳定平衡点,rad;δUEP为同步机不稳定平衡点,rad。
将同步机的转子运动方程两侧同时乘以Δω,经过移项、积分运算等步骤后,可以构建得到能量函数V。能量函数V的表达式为
其中:
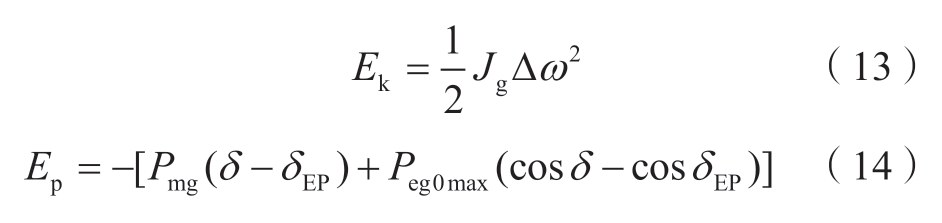
构建的能量函数V满足Lyapunov函数的定义时,需要满足以下3个条件:①系统平衡点是V的1个平稳点;②V在其中1个平衡点的邻域内是正定的;③V的导数是非正的。
第①个条件利用V的梯度ΔV来检验:
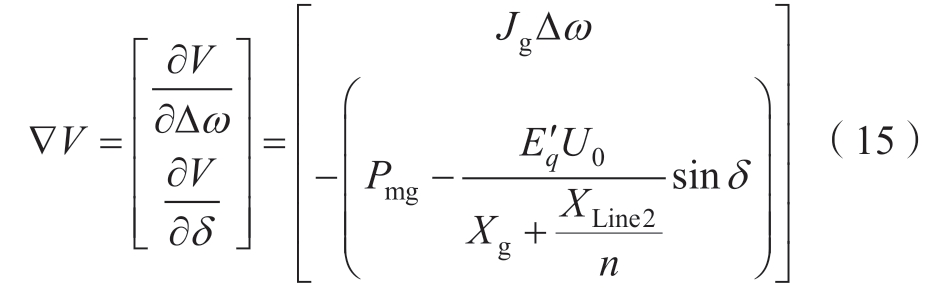
在设定的平稳点处, V=0,即能量函数V的梯度为0,满足Lyapunov平稳点的要求。
V=0,即能量函数V的梯度为0,满足Lyapunov平稳点的要求。
第②个条件利用Hessian矩阵来检验:
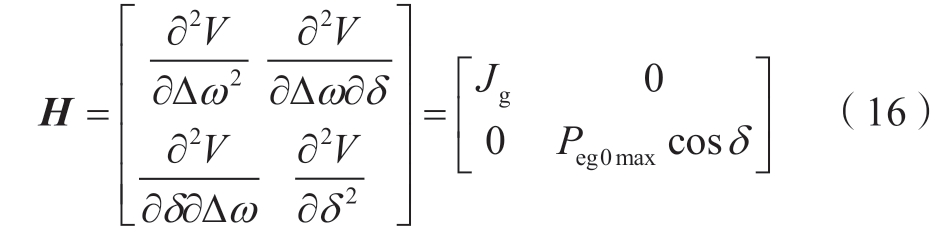
根据Sylvester定理,利用H矩阵判断正定的条件为:Jg>0且cosδ>0。由于Jg始终大于0,而cosδ在δSEP处为正、在δUEP处为负,因此该条件对δ=δSEP、Δω=0是成立的,即能量函数V在式(10)所对应平稳点处是正定的。
第③个条件利用考虑阻尼时的V的导数来进行检验:
由此得到的能量函数V的导数表示同步机功角所具有能量的耗散衰减速率。因此,能量函数V满足Lyapunov函数的导数非负这一条件。
在式(10)所示平稳点处,Ek、Ep、V可分别理解为功角相对于该平稳点所具有的动能、势能与总能量,因此取该点为能量函数V对应的平稳点。
3.2 送端系统的暂态稳定性评估
能量函数V的稳定临界值,即暂态稳定边界与不稳定平稳点δUEP上的V值对应,记为Vcr,有:
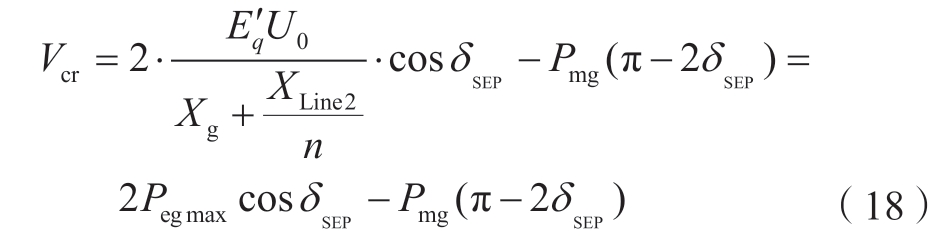
若δ0与Δω0表示某阶段暂态过程所对应的初始状态,不考虑阻尼与外部能量时,同步机稳定应满足的条件为
4 同步机容量比例对暂态稳定的影响
在图1 (a)所示的送端交流系统中,新能源场站与同步机电源通常由多回线路送出,在进行暂态稳定性校核时需要选择多回线同时故障:一方面,多回线路中的某一回线故障后,同步机机端残压高于多回线同时故障(暂态稳定性更好),计算暂态稳定性边界时,需要选择更为恶劣的多回线同时故障;另一方面,实际情况下存在多回送出线路同时发生故障的可能性。因此,考虑将2条送出线路都等效为线路阻抗一定的等效单回线路,等效单回线路故障就对应于多回线路同时故障。
现将换流器1、换流器2、同步机的容量分别记为S1N、S2N、Sg,用kSg表示同步机容量占换流器1容量的比例后,三者之间满足:
4.1 容量比例对暂态稳定边界的影响
当线路长度一定时,同步机的传输功率极限Peg max一定。δSEP与Pmg的关系为
由此,暂态稳定边界Vcr关于δSEP的导数为
当Peg max恒定时,δSEP随着Sg的增大而在(0,π/2)上增大,因此Vcr随着Sg的增大而减小。上述分析说明:当换流器1的容量S1N确定且线路参数一定时,同步机的装机容量Sg(对应于Sg占S1N的比例kSg)越大,Lyapunov能量函数V的稳定临界值Vcr越小,对应的Lyapunov稳定域边界也就越小。因此,kSg增大不利于系统的暂态稳定性。
4.2 容量比例对故障期间暂态过程的影响
φ2取-90°后(故障期间换流器2向交流系统注入无功电流),在故障i下,同步机电磁功率Pegi的表达式为
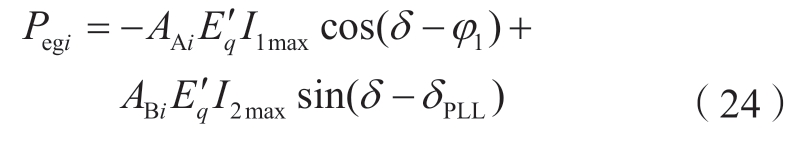
影响因子中,仅有AAi与ABi对故障态下的同步机电磁功率有影响,因此着重关注其取值。单回路系统中,故障态下的AAi与ABi表达式中仅有AA1不为0,其表达式为
AAi与ABi均不随kSg的变化而变化,因此kSg对故障态下的Pegi无影响。但增大kSg会同时增大Pmg,在Pegi无变化的情况下,同步机的净转矩将增大,V的轨迹到达稳定边界Vcr的时间(也即故障清除时间)将缩短,因此kSg增大将恶化同步机的暂态特性。
4.3 基于暂态稳定性的容量占比评估方法
以故障清除时间(critical clearing time,CCT)为量化指标时,kSg应当使系统任意点发生故障时的CCT不小于所期望的CCT值,即:系统最严重故障下的CCT为期望的CCT时,基于式(8)得到的对应kSg即为该期望CCT下最大的同步机容量占比。根据式(6),当换流站1在限流模式下的电流相角φ1有利于同步机的稳定性时,对同步机而言,线路1与线路2上的最严重故障均位于送端换流站的交流侧出口。因此,送端换流站的交流侧出口发生三相金属性接地故障时,使系统CCT为期望CCT值的kSg即为最大的同步机容量比例。
过大的同步机容量占比kSg对Lyapunov暂态稳定边界及故障暂态过程均有恶化作用,因此在不同期望CCT下,能使系统保持同步稳定的同步机最大容量比例kSg-max将随着期望CCT的增大而减小。
5 同步机容量比例对暂态稳定影响的数值计算结果
5.1 算例简介
基于图2所示的等值电路图,利用4.3节所提出的同步机容量占比评估方法,在不同期望CCT、不同送出线路长度下,对能使系统保持同步稳定的同步机最大容量比例kSg-max进行数值计算。其中,同步机与换流器2均满发,换流器2无功指令值为0;采用三回线输出的线路2等效为单回路;故障为三相金属性接地故障,且发生于换流器1的交流侧出口。系统其他主要参数如表1所示。
表1 系统主要参数
Table 1 Main parameters of the system
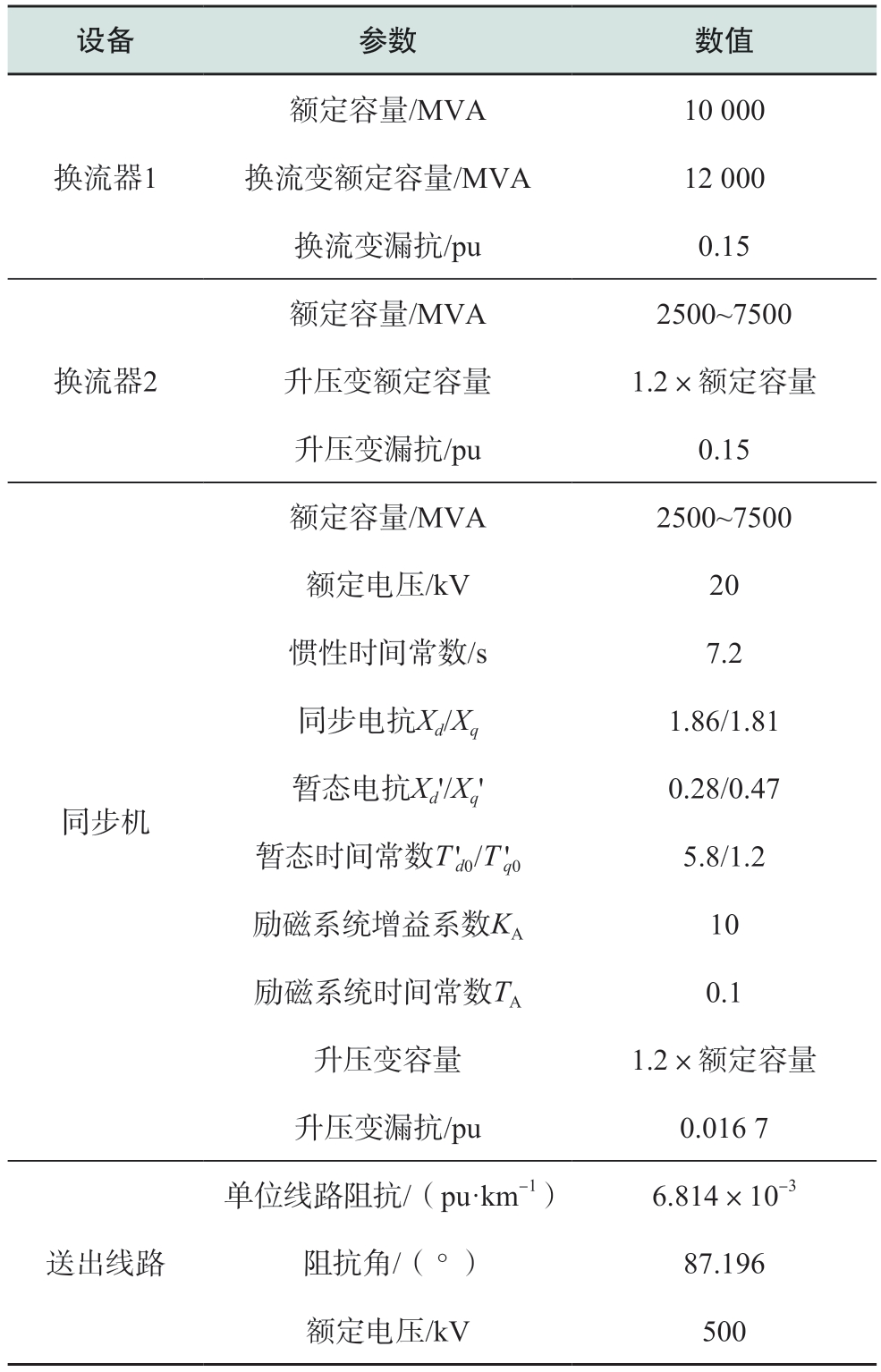
设备 参数 数值换流器1额定容量/MVA 10 000换流变额定容量/MVA 12 000换流变漏抗/pu 0.15换流器2额定容量/MVA 2500~7500升压变额定容量 1.2×额定容量升压变漏抗/pu 0.15同步机额定容量/MVA 2500~7500额定电压/kV 20惯性时间常数/s 7.2同步电抗Xd/Xq 1.86/1.81暂态电抗Xd'/Xq' 0.28/0.47暂态时间常数T'd0/T'q0 5.8/1.2励磁系统增益系数KA 10励磁系统时间常数TA 0.1升压变容量 1.2×额定容量升压变漏抗/pu 0.016 7送出线路单位线路阻抗/(pu·km-1) 6.814×10-3阻抗角/(°) 87.196额定电压/kV 500
5.2 容量比例对暂态稳定性影响的解析分析
在期望CCT为100 ms、线路2长度l2=420 km的条件下:图3 (a) 显示,随着kSg提升,稳定边界的上、下、左、右边界极值 (分别记作Δωup、Δωdown、δleft、δright)均向着稳定区域缩小的方向变化;图3 (b) 显示,随着kSg提升,暂态稳定边界逐渐缩小,故障期间的功角变化逐渐加快。二者的变化规律均说明了同步机容量比例增加对系统暂态特性具有恶化作用,也印证了第4章理论分析的正确性。
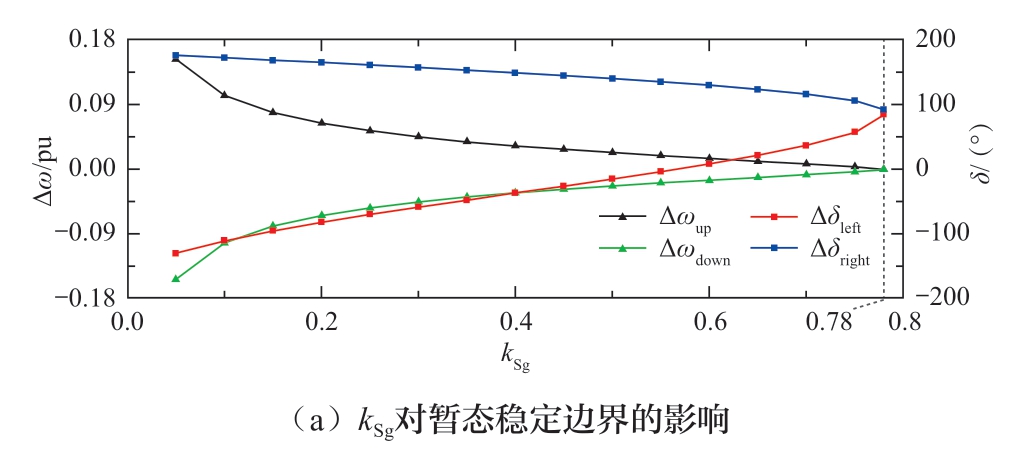
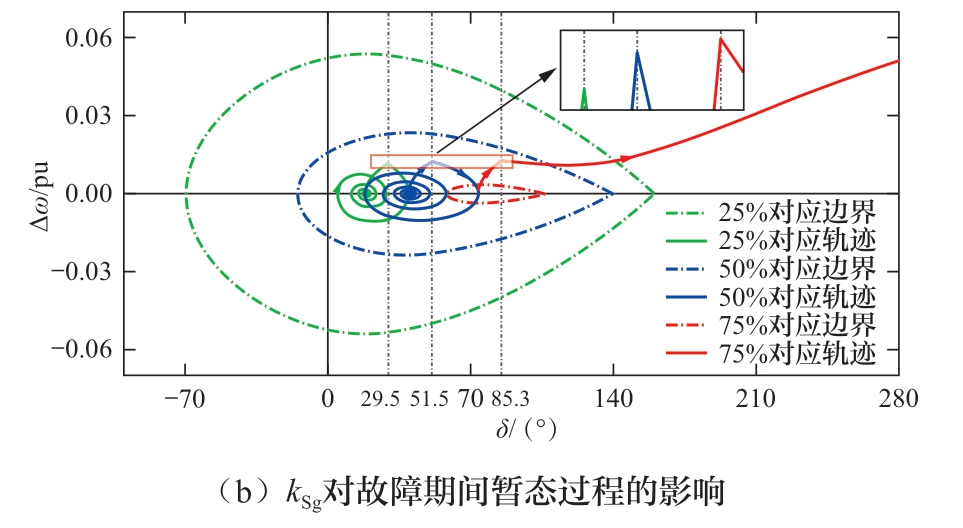
图3 同步机容量占比kSg对暂态稳定性的影响
Fig.3 Influence of synchronous machine capacity proportion kSg on transient stability characteristics
本文针对期望CCT对同步机最大容量占比kSg-max的影响开展解析分析时,选取的线路2长度分别为300 km、420 km,并将kSg-max随期望CCT变化的解析结果绘制于图4中。据图4所示,随着期望CCT的提升,kSg-max逐渐减小。因此,在送端换流站采用V/f控制策略的情况下,若系统易发生持续时间相对较长的故障时,送端的同步机电源占比应相对较低。
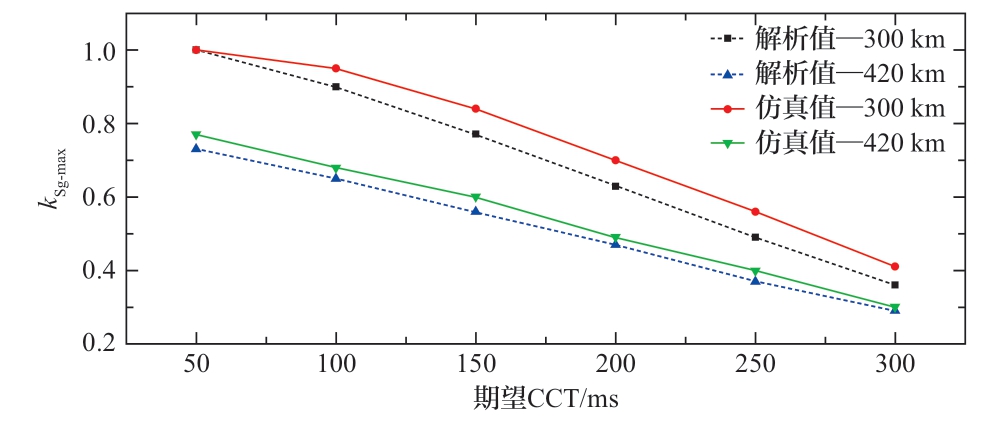
图4 不同期望CCT下的同步机最大容量比例kSg-max
Fig.4 The maximum capacity proportion kSg-max of synchronous generator under different expected CCTs
在给定线路参数下,线路2阻抗由其长度l2决定,因此在研究线路2阻抗对同步机最大容量占比kSg-max的影响时,分别以期望CCT为100 ms、期望CCT为200 ms为例,将kSg-max随l2变化的趋势绘制于图5中。据图5所示,随着线路2的增长,能使系统保持同步稳定的kSg-max逐渐减小。因此,在送端换流站采用V/f控制策略的工况下,为保证送端系统的暂态稳定性,当同步机电源送出线路的阻抗较大时,同步机电源占比应相对较低。
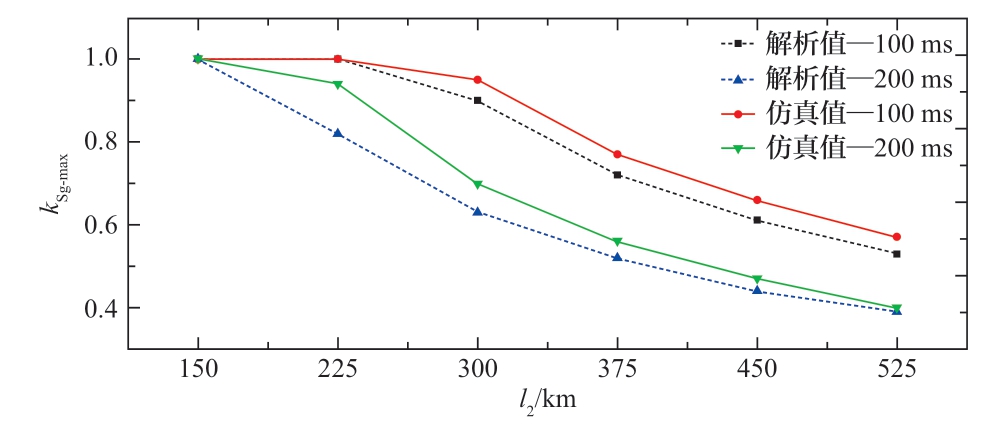
图5 不同线路2长度下的同步机最大容量比例kSg-max
Fig.5 The maximum capacity proportion kSg-max of synchronous generator under different lengths of Line 2
以上解析结果说明:同步机容量占比增加将恶化系统的暂态特性,不利于送端系统实现故障穿越,在同步机容量占比过高的情况下,送端换流站V/f控制策略的应用将受到限制,这与第4章理论分析结果一致。
6 仿真验证
本文在PSCAD平台中基于图2搭建了仿真测试系统,以验证研究分析的正确性及所提方法的有效性。测试系统的工况与5.1节数值计算所采用的算例一致,系统主要参数如表1所示。其中,同步机采用6阶模型,三相金属性接地故障均在7.0 s时发生于换流器1的交流侧出口。
为验证期望CCT对同步机最大容量占比的影响,测试系统分别选取长度为300 km、420 km的同步机送出线路开展仿真验证,同步机最大容量占比的数值计算与时域仿真结果对比如图4所示。
图4所示的数值计算结果与时域仿真结果反映了期望CCT与同步机最大容量占比之间的关系,均说明期望CCT的增大将导致同步机的最大容量占比逐渐下降;由于解析计算采用的同步机2阶模型忽略了同步机励磁系统等对同步机暂态稳定性的增强作用,利用所提方法得到的数值计算结果比时域仿真结果更具保守性,但二者间的误差基本在10%以内,所提方法仍具有较高精确性。
为验证同步机送出线路阻抗对同步机最大容量占比的影响,测试系统分别选取期望CCT为100 ms、期望CCT为200 ms的工况开展仿真验证,同步机最大容量占比的数值计算与时域仿真结果对比如图5所示。
图5显示,利用本文所提方法得到的数值计算结果与时域仿真结果均说明:同步机送出线路阻抗增大时,能保持系统同步稳定的同步机最大容量占比逐渐下降。同样地,通过解析得到的数值计算结果比时域仿真结果更具保守性,基于该数值进行工程规划,能在一定程度上增大系统实际的暂态稳定裕度。
本文针对不同期望CCT与线路2长度开展了仿真测试,将部分仿真结果绘制于图6中。根据图6的同步机功角变化波形可知,送端系统同步机的失稳形式表现为同步机与采用V/f控制的送端换流站之间发生功角失稳。
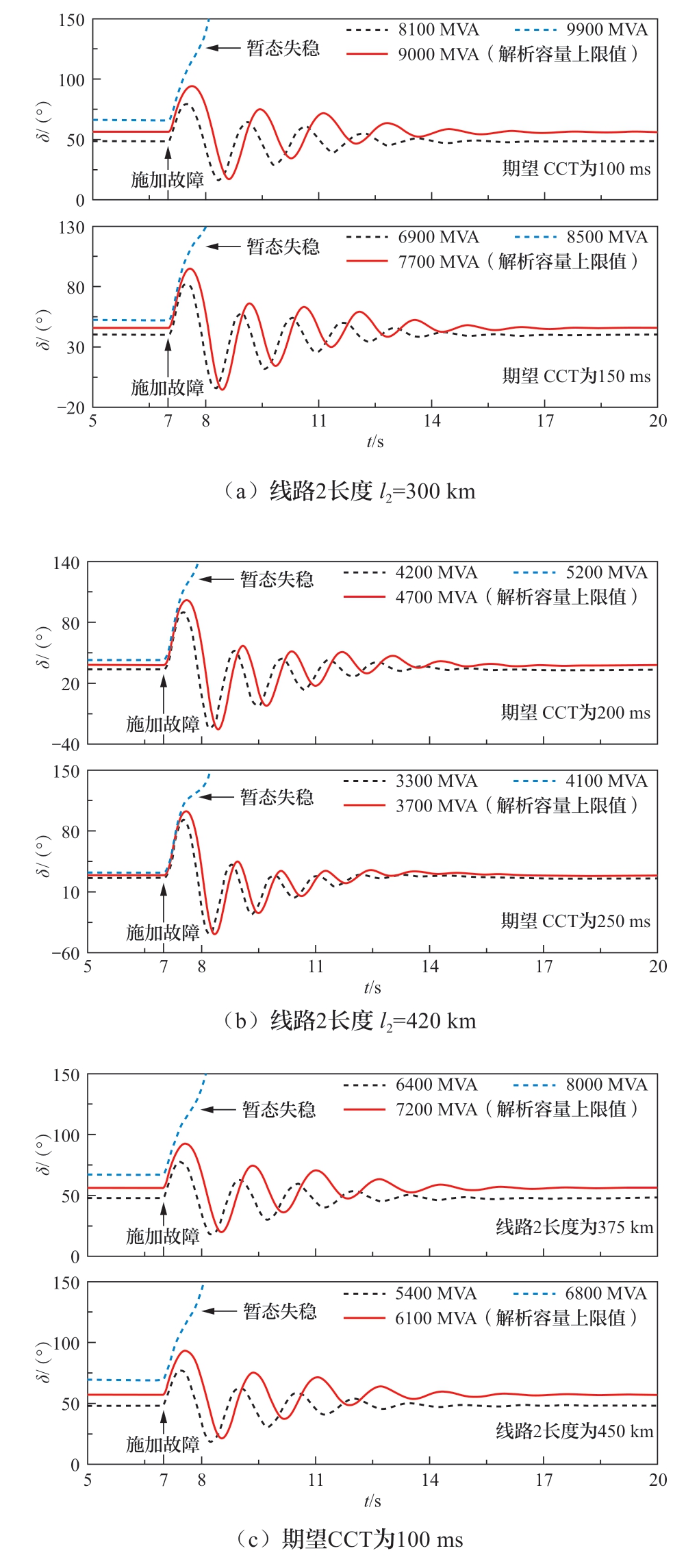
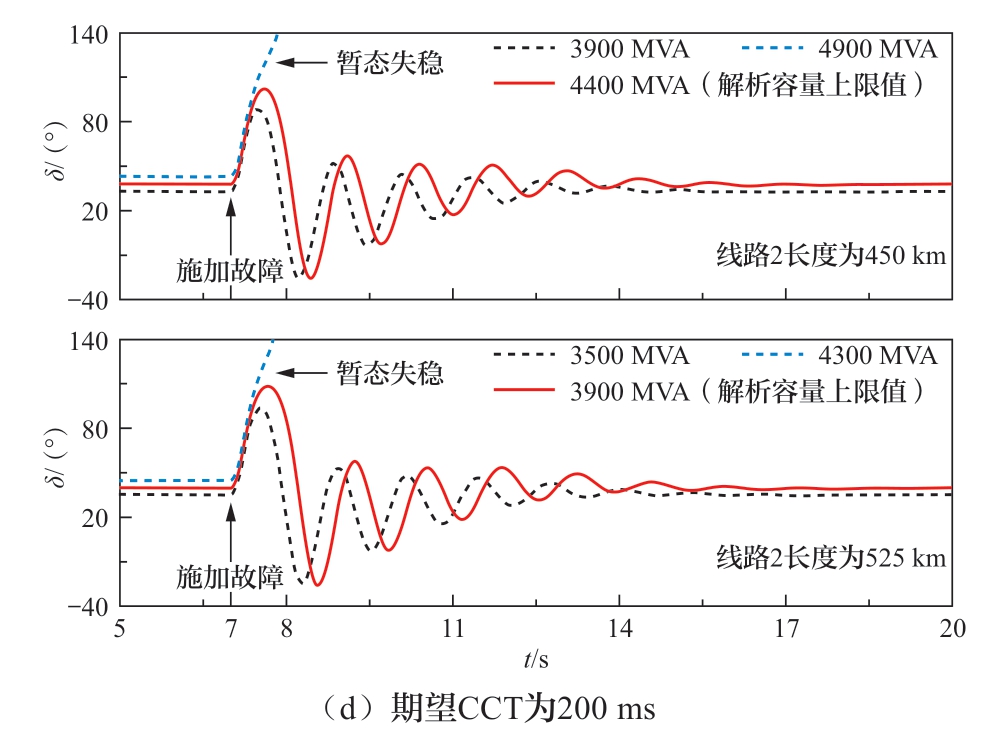
图6 不同线路2长度、期望CCT下的同步机功角波形图
Fig.6 Power angle waveforms of synchronous machines under different lengths of Line 2 and different expected CCTs
基于图6所示波形图可知,仿真系统中的同步机在其容量占比小于解析值10%或等于解析值时能够保持同步稳定,在其容量占比大于解析值10%时失去同步,进一步印证了同步机容量占比过大不利于送端系统暂态稳定性的结论,也证明了解析结果相对于仿真结果的保守性。
此外,在期望CCT为200 ms、l1=150 km、l2=375 km的工况下,不同故障位置、不同故障类型下的kSg-max仿真结果记于表2与表3中。
表2 不同三相金属性接地故障位置下的kSg-max
Table 2 kSg-max of three-phase metallic grounding faults at different locations

三相金属性接地故障位置kSg-max(<1)某一回线故障 三回线同时故障k1=0.5 0.77 0.70 k2=0.5 0.90 0.56 PCC1 0.56(某一回线故障与三回线同时故障等价)
表3 PCC1处不同故障类型下的kSg-max
Table 3 kSg-max under different fault types at PCC1

PCC1处故障类型 kSg-max(<1)单相金属性接地故障 0.99两相金属性接地故障 0.72三相金属性接地故障 0.56
如表2所示,多回线同时故障下的kSg-max更小,表明其严重性高于某一回线故障;如表2与表3所示,PCC1处三相金属性接地故障下的kSg-max最小,说明这一故障位置与故障类型对应的故障最为严重。以上结果均印证了相应假设的合理性与正确性,证明了依据所提方法得到的kSg-max能确保系统在不同位置与类型的故障下均不发生暂态失稳。
7 结论
本文基于能量型Lyapunov函数法研究了同步机电源容量占比对新能源联合水电、火电等同步机电源经柔直送出系统暂态稳定性的影响,并基于此提出了容量占比的评估方法。本文的主要研究结论如下。
1)同步机容量占比过大不利于系统的暂态稳定性。一方面,能量型Lyapunov函数的稳定临界值随同步机容量占比的提升而减小;另一方面,同步机容量占比的提升将增大同步机的净转矩,缩短能量型Lyapunov函数到达暂态稳定临界能量的时间。在同步机容量占比过高的情况下,V/f控制策略不再适用于送端换流站。
2)若系统易发生持续时间相对较长的故障或同步机电源送出线路的阻抗较大时,为保证送端系统的暂态稳定性,同步机电源占比应相对较低。
3)基于本文所提的容量占比评估方法,可解析得到能保持系统同步稳定的同步机电源最大容量占比,由于忽略了同步机励磁系统等因素,该方法所得结果比时域仿真结果更为保守。但基于该数值进行工程规划,能在一定程度上增大系统实际的暂态稳定裕度。
针对上述送端系统,本文揭示了送端整流站V/f控制策略在高同步机电源占比下的应用局限性,因此未来亟须围绕系统控制策略的优化设计开展研究,增强送出系统对不同电源配比的适应能力,进一步实现新型电力系统对能源的灵活配置。
参考文献
-
[1]
贺之渊,杨杰,吴亚楠,等.能源转型下的未来交流和直流联合运行模式及发展趋势探讨 [J].中国电机工程学报,2023,43(1):99-114.HE Zhiyuan, YANG Jie, WU Yanan, et al.Investigation on the future AC and DC combined operation form and development trend under energy transition[J].Proceedings of the CSEE,2023, 43(1): 99-114(in Chinese). [百度学术]
-
[2]
王国法,刘合,王丹丹,等.新形势下我国能源高质量发展与能源安全[J].中国科学院院刊,2023,38(1):23-37.WANG Guofa, LIU He, WANG Dandan, et al.Highquality energy development and energy security under the new situation for China[J].Bulletin of Chinese Academy of Sciences, 2023, 38(1): 23-37(in Chinese). [百度学术]
-
[3]
单葆国,刘青,张莉莉,等.新形势下“十四五”后三年中国电力需求形势研判[J].中国电力,2023,56(3):1-11.SHAN Baoguo, LIU Qing, ZHANG Lili, et al.Analysis of China’s power demand situation in the last three years of the “14th Five-Year Plan” under the new situation[J].Electric Power, 2023, 56(3): 1-11(in Chinese). [百度学术]
-
[4]
王朋,张迪,张勇军,等.新型电力系统数智化关键技术应用研究与展望[J].电力系统保护与控制,2025,53(6):175-187.WANG Peng, ZHANG Di, ZHANG Yongjun, et al.Application research and prospect of key technologies of digital intelligence in new power system[J].Power System Protection and Control, 2025, 53(6): 175-187(in Chinese). [百度学术]
-
[5]
黄河,王建学,肖云鹏,等.新型电力系统电力电量平衡分析关键技术与研究框架[J].电力建设,2024,45(9):1-12.HUANG He, WANG Jianxue, XIAO Yunpeng, et al.Key technologies and research framework of power balance analysis in new power system[J].Electric Power Construction,2024, 45(9): 1-12(in Chinese). [百度学术]
-
[6]
张祖菡,刘敦楠,凡航,等.基于大语言模型的电力系统预测技术研究综述[J].发电技术,2025,46(3):438-453.ZHANG Zuhan, LIU Dunnan, FAN Hang, et al.Overview of power system forecasting technology based on large language model[J].Power Generation Technology, 2025, 46(3): 438-453(in Chinese). [百度学术]
-
[7]
牟长兴,张俊涛,程春田,等.考虑时空相关性的流域水风光多能互补系统高维不确定性场景生成方法 [J].电网技术,2024,48(9):3614-3623.MOU Changxing, ZHANG Juntao, CHENG Chuntian, et al.High-dimensional uncertainty scenario generation method for hydro-wind-solar multi-energy complementary system considering spatio-temporal correlation[J].Power System Technology, 2024, 48(9): 3614-3623(in Chinese). [百度学术]
-
[8]
中华人民共和国政府网.我国西部清洁能源基地加快建设[EB/OL].(2024-06-16)[2025-02-26].http://www.gov.cn/yaowen/shipin/202406/content_6957637.htm. [百度学术]
-
[9]
刘泽洪,周原冰,李隽,等.中国西北西南电网互联研究[J].全球能源互联网,2023,6(4):341-352.LIU Zehong, ZHOU Yuanbing, LI Jun, et al.Research on interconnection of northwest southwest power grid in China[J].Journal of Global Energy Interconnection, 2023, 6(4): 341-352(in Chinese). [百度学术]
-
[10]
中华人民共和国政府网.我国西部地区能源基地加快建设新能源装机总规模占全国四成左右[EB/OL].(2024-06-18)[2025-02-26].http://www.gov.cn/lianbo/bumen/202406/content_6957858.htm. [百度学术]
-
[11]
栗峰,丁杰,周才期,等.新型电力系统下分布式光伏规模化并网运行关键技术探讨[J].电网技术,2024,48(1):184-199.LI Feng, DING Jie, ZHOU Caiqi, et al.Key technologies of large-scale grid-connected operation of distributed photovoltaic under new-type power system[J].Power System Technology,2024, 48(1): 184-199(in Chinese). [百度学术]
-
[12]
李晖,刘栋,姚丹阳.面向碳达峰碳中和目标的我国电力系统发展研判[J].中国电机工程学报,2021,41(18):6245-6259.LI Hui, LIU Dong, YAO Danyang.Analysis and reflection on the development of power system towards the goal of carbon emission peak and carbon neutrality[J].Proceedings of the CSEE, 2021, 41(18): 6245-6259(in Chinese). [百度学术]
-
[13]
李响,武海潮,王文雪,等.考虑大规模新能源接入的电网性能评价指标体系[J].电力系统保护与控制,2024,52(15):178-187.LI Xiang, WU Haichao, WANG Wenxue, et al.Performance evaluation index system of a power grid considering largescale new energy[J].Power System Protection and Control,2024, 52(15): 178-187 (in Chinese). [百度学术]
-
[14]
范宏,李婷,严嘉鑫,等.基于按需比例分配机制的风光火氢多时间尺度协同规划[J].电力工程技术,2024,43(2):33-43.FAN Hong, LI Ting, YAN Jiaxin, et al.Multi-time scale collaborative planning of wind, light, fire and hydrogen based on on-demand proportional distribution mechanism[J].Electric Power Engineering Technology, 2024, 43(2): 33-43(in Chinese). [百度学术]
-
[15]
孙浩男,杜鹏,刘念,等.大规模风光储场站群功率跟踪优化控制实时仿真[J].电力建设,2024,45(8):62-74.SUN Haonan, DU Peng, LIU Nian, et al.Real-time simulation of optimal power tracking control for large-scale windphotovoltaic-storage power station clusters[J].Electric Power Construction, 2024, 45(8): 62-74(in Chinese). [百度学术]
-
[16]
赵心怡,谢俊,周翠玉,等.风-光-抽蓄零碳电力系统多时间尺度协调调度模型[J].电力工程技术,2023,42(3):121-129.ZHAO Xinyi, XIE Jun, ZHOU Cuiyu, et al.A multi-time scale coordinated dispatching model of wind-photovoltaicpumped storage zero-carbon power system[J].Electric Power Engineering Technology, 2023, 42(3): 121-129(in Chinese). [百度学术]
-
[17]
国家能源局.国家能源局发布2025年1-3月份全国电力工业统计数据[EB/OL].(2025-04-20)[2025-05-07].https://www.nea.gov.cn/20250420/ea90b16331c446a1bad218c4b3c0df7d/c.html. [百度学术]
-
[18]
张俊涛,程春田,于申,等.水电支撑新型电力系统灵活性研究进展、挑战与展望[J].中国电机工程学报,2024,44(10):3862-3885.ZHANG Juntao, CHENG Chuntian, YU Shen, et al.Progress,challenges and prospects of research on hydropower supporting the flexibility of new power systems[J].Proceedings of the CSEE, 2024, 44(10): 3862-3885(in Chinese). [百度学术]
-
[19]
乔丰翔,陆涛,周晓鸣.考虑电碳协同的火电发电商中长期交易策略[J].电力需求侧管理,2024,26(5):106-112.QIAO Fengxiang, LU Tao, ZHOU Xiaoming.Mediumand long-term trading bidding strategies for thermal power producers considering electricity-carbon synergies[J].Power Demand Side Management, 2024, 26(5): 106-112(in Chinese). [百度学术]
-
[20]
李展,杨振勇,刘磊,等.火电机组深度调峰工况下炉侧蓄热系数对一次调频能力的影响分析[J].发电技术,2024,45(2):226-232.LI Zhan, YANG Zhenyong, LIU Lei, et al.Analysis of the influence of furnace side heat storage coefficient on primary frequency modulation capacity under deep modulation condition of thermal power unit[J].Power Generation Technology, 2024, 45(2): 226-232(in Chinese). [百度学术]
-
[21]
王放放,杨鹏威,赵光金,等.新型电力系统下火电机组灵活性运行技术发展及挑战[J].发电技术,2024,45(2):189-198.WANG Fangfang, YANG Pengwei, ZHAO Guangjin, et al.Development and challenge of flexible operation technology of thermal power units under new power system[J].Power Generation Technology, 2024, 45(2): 189-198(in Chinese). [百度学术]
-
[22]
王义民,刘世帆,李婷婷,等.雅砻江能源基地水风光互补短期调度运行模式对比研究[J].水利学报,2023,54(4):439-450.WANG Yimin, LIU Shifan, LI Tingting, et al.Comparative study on short-term dispatching operation mode of Yalong River energy base with complementary water, wind and light[J].Journal of Hydraulic Engineering, 2023, 54(4): 439-450(in Chinese). [百度学术]
-
[23]
杨丽娜.我国大宗能源开发利用的分布格局及其时空变化[D].兰州:兰州大学,2012.YANG Lina.Distribution pattern and temporal and spatial changes of bulk energy development and utilization in China[D].Lanzhou: Lanzhou University, 2012(in Chinese). [百度学术]
-
[24]
徐政,肖晃庆,张哲任,等.柔性直流输电系统[M].2版.北京:机械工业出版社,2017.XU Zheng, XIAO Huangqing, ZHANG Zheren, et al.Flexible DC transmission system[M].2nd ed.Beijing: China Machine Press, 2017(in Chinese). [百度学术]
-
[25]
FLOURENTZOU N, AGELIDIS V G, DEMETRIADES G D.VSC-based HVDC power transmission systems: an overview[J].IEEE Transactions on Power Electronics, 2009,24(3): 592-602. [百度学术]
-
[26]
王硕,何柏娜,程婷,等.MMC-HVDC双极故障条件下自适应限流控制策略[J].电力工程技术,2024,43(6):53-63.WANG Shuo, HE Baina, CHENG Ting, et al.Adaptive current limiting control strategy under MMC-HVDC bipolar fault condition[J].Electric Power Engineering Technology, 2024,43(6): 53-63(in Chinese). [百度学术]
-
[27]
郑少明,刘一民,董鹏,等.张北工程风电柔直汇集系统次、超同步振荡分析[J].全球能源互联网,2023,6(6):608-617.ZHENG Shaoming, LIU Yimin, DONG Peng, et al.Analysis of sub/super-synchronous oscillation between wind farm and MMC in Zhangbei project[J].Journal of Global Energy Interconnection, 2023, 6(6): 608-617(in Chinese). [百度学术]
-
[28]
魏兴杰,张英敏,刘坤,等.半桥型MMC直流侧故障限流组合控制策略[J].电力工程技术,2023,42(1):209-217.WEI Xingjie, ZHANG Yingmin, LIU Kun, et al.Combined control strategy of fault current limiting on DC side of halfbridge MMC[J].Electric Power Engineering Technology,2023, 42(1): 209-217(in Chinese). [百度学术]
-
[29]
马文龙,王程,毕天姝.支撑受端频率的水光互补新能源基地-多端柔直协同控制方法 [J].中国电机工程学报,2025,45(2):1-17.MA Wenlong, WANG Cheng, BI Tianshu.Cooperative control method of hydro-photovoltaic complementary renewable generation base-MTDC system supporting the frequency of the receiving-end[J].Proceedings of the CSEE, 2025, 45(2):1-17(in Chinese). [百度学术]
-
[30]
刘会强,辛力坚,张爱军,等.多运行方式下风光火打捆外送系统小干扰稳定性分析[J].智慧电力,2025,53(2):25-31.LIU Huiqiang, XIN Lijian, ZHANG Aijun, et al.Small signal stability analysis of multi-operation wind-light-fire bundling and delivery system[J].Smart Power, 2025, 53(2): 25-31(in Chinese). [百度学术]
-
[31]
张舒文,郭春义,赵薇,等.水光互补柔性直流外送系统的功率传输能力研究 [J].中国电机工程学报,2024,44(9):1-13.ZHANG Shuwen, GUO Chunyi, ZHAO Wei, et al.Research on the power transmission capability of PV-hydro complementary MMC-HVDC transmission system[J].Proceedings of the CSEE, 2024, 44(9): 1-13(in Chinese). [百度学术]
-
[32]
申建建,王月,程春田,等.水风光多能互补发电调度问题研究现状及展望[J].中国电机工程学报,2022,42(11):3871-3885.SHEN Jianjian, WANG Yue, CHENG Chuntian, et al.Research status and prospect of water, wind and solar energy complementary power generation scheduling problem[J].Proceedings of the CSEE, 2022, 42(11): 3871-3885(in Chinese). [百度学术]
-
[33]
冷若寒,庄可好,侯智贤,等.考虑跟网型新能源低电压穿越特性的构网型变流器功能定位与容量优化配置[J].中国电机工程学报,2025,45(2):1-11.LENG Ruohan, ZHUANG Kehao, HOU Zhixian, et al.Functional positioning and capacity optimized allocation of grid-forming converter considering low voltage ride through of grid-following new energy station[J].Proceedings of the CSEE, 2025, 45(2): 1-11(in Chinese). [百度学术]
-
[34]
周建力.风-光-氢综合能源系统容量配置优化及决策模型研究[D].北京:华北电力大学,2022. [百度学术]
-
[35]
辛焕海,王宇轩,刘晨曦,等.提高新能源场站稳定性的构网型与跟网型变流器容量配比估算[J].中国电机工程学报,2024,44(14):5463-5473.XIN Huanhai, WANG Yuxuan, LIU Chenxi, et al.Estimation of capacity ratios between grid-forming and grid-following converters for improving the stability of renewable energy stations[J].Proceedings of the CSEE, 2024, 44(14): 5463-5473(in Chinese). [百度学术]
-
[36]
徐政.新型电力系统背景下电网强度的合理定义及其计算方法[J].高电压技术,2022,48(10):3805-3819.XU Zheng.Reasonable definition and calculation method of power grid strength under the background of new type power systems[J].High Voltage Engineering, 2022, 48(10): 3805-3819(in Chinese). [百度学术]
-
[37]
郭铭群,梅念,李探,等.±500 kV张北柔性直流电网工程系统设计 [J].电网技术,2021,45(10):4194-4204.GUO Mingqun, MEI Nian, LI Tan, et al.System design of±500 kV Zhangbei VSC-based DC grid project [J].Power System Technology, 2021, 45(10): 4194-4204(in Chinese). [百度学术]
-
[38]
李宇骏,华凤林,陆艺源,等.基于李雅普诺夫函数的带锁相环的VSC大扰动稳定性判据[J].电力系统保护与控制,2023,51(2):46-54.LI Yujun, HUA Fenglin, LU Yiyuan, et al.Large disturbance stability criterion of VSC with phase-locked loop based on Lyapunov function[J].Power System Protection and Control,2023, 51(2): 46-54(in Chinese). [百度学术]
-
[39]
SHUAI Z K, SHEN C, LIU X, et al.Transient angle stability of virtual synchronous generators using Lyapunov’s direct method[J].IEEE Transactions on Smart Grid, 2019, 10(4):4648-4661. [百度学术]
-
[40]
柳劲松,马宁宁,刘舒.高比例风电系统宽频振荡紧急控制策略研究[J].全球能源互联网,2024,7(5):558-566.LIU Jinsong, MA Ningning, LIU Shu.Study on emergency control strategy of wideband oscillation in power systems with high-percentage wind power[J].Journal of Global Energy Interconnection, 2024, 7(5): 558-566(in Chinese). [百度学术]
-
[41]
沈赋,李施伟,王健,等.融合储能的光伏发电系统并网逆变器建模与稳定性分析[J].电力系统保护与控制,2024,52(19):131-143.SHEN Fu, LI Shiwei, WANG Jian, et al.Modeling and stability analysis of a photovoltaic grid-connected inverter integrated with an energy storage system[J].Power System Protection and Control, 2024, 52(19): 131-143 (in Chinese). [百度学术]
-
[42]
TAUL M G, WANG X F, DAVARI P, et al.Current limiting control with enhanced dynamics of grid-forming converters during fault conditions[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1062-1073. [百度学术]
-
[43]
薛翼程,王国腾,张哲任,等.MMC-HVDC接入对同步发电机阻尼转矩的影响机理分析[J].电力系统自动化,2022,46(9):99-108.XUE Yicheng, WANG Guoteng, ZHANG Zheren, et al.Mechanism analysis of influence of MMC-HVDC connection on damping torque of synchronous generator[J].Automation of Electric Power Systems, 2022, 46(9): 99-108(in Chinese). [百度学术]
-
[44]
杨银国,林旭,吴国炳,等.构网型、跟网型非同步机电源并网系统暂态同步稳定性分析[J].太阳能学报,2024,45(8):218-228.YANG Yinguo, LIN Xu, WU Guobing, et al.Analysis of transient synchroniiation stability of power system with gridforming/grid-following nonsynchronous-machine sources[J].Acta Energiae Solaris Sinica, 2024, 45(8): 218-228(in Chinese). [百度学术]
-
[45]
黄林彬,辛焕海,鞠平,等.电力电子并网装备的同步稳定分析与统一同步控制结构[J].电力自动化设备,2020,40(9):10-25.HUANG Linbin, XIN Huanhai, JU Ping, et al.Synchronization stability analysis and unified synchronization control structure of grid-connected power electronic devices[J].Electric Power Automation Equipment, 2020, 40(9): 10-25(in Chinese). [百度学术]
-
[46]
项中明,倪秋龙,李振华,等.跟网型MMC-HVDC并网暂态同步稳定机理分析[J].电气工程学报,2023,18(3):250-259.XIANG Zhongming, NI Qiulong, LI Zhenhua, et al.Transient stability mechanism analysis of grid-following MMCHVDC[J].Journal of Electrical Engineering, 2023, 18(3): 250-259(in Chinese). [百度学术]
-
[47]
HU Q, FU L J, MA F, et al.Large signal synchronizing instability of PLL-based VSC connected to weak AC grid[J].IEEE Transactions on Power Systems, 2019, 34(4): 3220-3229. [百度学术]
-
[48]
GOLESTAN S, GUERRERO J M, VASQUEZ J C.A robust and fast synchronization technique for adverse grid conditions[J].IEEE Transactions on Industrial Electronics,2017, 64(4): 3188-3194. [百度学术]
-
[49]
WU H, WANG X F.Design-oriented transient stability analysis of PLL-synchronized voltage-source converters[J].IEEE Transactions on Power Electronics, 2020, 35(4): 3573-3589. [百度学术]
基金项目
国家自然科学基金项目(U23B6008)。
National Natural Science Foundation of China (U23B6008).


