相关论文:
-

-
全球能源互联网
第8卷 第6期 2025年11月;页码:690-701
基于定直流电压及定功率控制并联结构的双受端VSC-HVDC系统稳定性分析
Stability Analysis of Dual-terminal VSC-HVDC System Based on Combined Constant DC Voltage and Constant Power Control
- 1.国网江苏省电力有限公司电力科学研究院,江苏省 南京市 211103
- 2.东南大学电气工程学院,江苏省 南京市 210096
- 3.国网江苏省电力有限公司,江苏省 南京市 210000
- BIN Zijun1, KONG Xiangping1, ZHAO Kai2, ZHENG Chaohang2, REN Xuchao3, TAO Yan1, WU Xi2* (1.Electric Power Research Institute, State Grid Jiangsu Electric Power Co., Ltd., Nanjing 211103, Jiangsu Province, China
- 2.School of Electrical Engineering, Southeast University, Nanjing 210096, Jiangsu Province, China
- 3.State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210000, Jiangsu Province, China
关键词
Keywords
摘 要
Abstract
电压源型直流输电系统(voltage source converter based high voltage direct current,VSC-HVDC)并入弱交流电网可能产生振荡失稳现象,严重威胁电力系统安全稳定运行。VSC-HVDC结构日渐复杂,系统中同时存在多种控制策略,针对多端、多控制策略下VSC-HVDC的稳定特性还需深入研究。针对上述问题,以定直流电压/定功率混合控制的双受端VSC-HVDC系统为研究对象,探讨了系统在不同电网条件下的稳定特性。首先,分别推导了定直流电压/定功率控制策略VSC-HVDC子系统的数学模型和小信号模型,依据交直流拓扑关系构建混合控制策略下的全系统模型;其次,搭建双受端VSC-HVDC系统电磁暂态模型验证了不同运行工况下小信号模型的准确性;最后,分析了交流系统强度及联络线长度对双受端VSC-HVDC系统稳定性的影响,获得了定直流电压/定功率VSC-HVDC系统所能接受的最小电网强度,形成了系统安全稳定运行空间,并且基于MATLAB/Simulink时域仿真验证了理论分析的正确性。
The integration of voltage source converter based high voltage direct current (VSC-HVDC) into weak AC power system may lead to oscillation and instability, which seriously threatens the safe and stable operation of power system.The structure of VSC-HVDC is becoming increasingly complex with multiple control strategies while further research is needed on the stability characteristics of VSC-HVDC under multi terminal and multi control strategies.In order to solve the issues mentioned above, in this paper, the stability of a dualterminal VSC-HVDC system with DC voltage and power hybrid control is analyzed under different grid conditions.Firstly,the mathematical model and the small signal model of VSCHVDC subsystems with DC voltage control and power control strategy are derived respectively.Based on AC/DC topology relationship, a global system model with hybrid control strategy is constructed.Secondly, the electromagnetic transient model of two-terminal VSC-HVDC system is constructed to verify the accuracy of small signal model under different operating conditions.Finally, the influence of AC system strength and tie line length on the stability of two-terminal VSC-HVDC system is analyzed, and the minimum AC system strength feasible for VSC-HVDC subsystems is obtained, thus forming the feasible region of system.The accuracy of theoretical analysis is verified through time domain simulation based on MATLAB/Simulink.
0 引言
柔性直流输电系统通过对换流器的灵活控制,可实现功率潮流反转迅速、电能的稳定输送和优化分配,进而推进能源的高效利用和低碳发展,因此在可再生能源发电并网、多地区系统互联等领域取得了广泛应用[1-5]。电压源型换流器(voltage source converter,VSC)作为典型的电力电子变换装置,其动态特征对于系统的稳定性具有重要影响。近年来,多个地区频繁发生VSC-HVDC振荡脱网事故。2015年,厦门±320 kV柔直工程送端单极输送100 MW和500 MW时,直流电流出现次同步振荡现象[6]。2013年,南澳多端柔性直流输电示范工程在新能源经柔性直流送出进行调试时,交直流电流存在明显的振荡失稳现象[7-9]。2017年,鲁西直流工程一端的柔性直流换流站接入交流弱网时,系统出现了高频振荡现象[10]。2018年,渝鄂直流背靠背联网工程在南通道的空载加压试验中出现网侧电压电流高频谐振现象[11]。2021年,如东海上风电柔直送出工程投运以来发生了多起振荡事故,导致系统谐波保护动作跳闸[12]。2022年,张北柔直工程运行期间,风速变化带来的直流电压骤变引起了直流电流振荡,并通过换流器耦合到交流系统,交直流系统中数次出现次/超同步振荡问题[13-14]。2022年白鹤滩—江苏特高压混合级联直流输电工程投运后,文献[15]在理论层面分析了白江混合级联柔性直流输电系统潜在的振荡模态,并指出定电压控制下的柔直换流器与系统中其他换流器以及交流系统之间存在耦合交互,系统稳定性下降。随着柔性直流输电技术在大规模跨区域等场景的应用,振荡失稳已经成为制约VSC-HVDC发展的关键问题。
针对柔直系统的振荡失稳问题,文献[16]通过扫频测量建立了系统阻抗模型,分析得到送端换流器电压控制比例增益设置偏小或者锁相环比例增益设置偏大可能引发系统次/超同步振荡。文献[17]建立了采用交流电压控制和定有功功率的VSC-HVDC小信号模型,分析了PLL带宽和控制器内外环带宽的交互作用,指出内外环交互作用在弱电网下更加明显,PLL带宽和外环q轴带宽应保持反比关系以改善系统稳定性。文献[18]分析了不同交流系统强度和控制参数下交流电压控制对直流电压控制稳定性的影响,并指出由交流电压控制的滞后效应所产生的额外负阻尼分量会随着交流系统强度的降低或输出功率的增加而增加,可以通过增大交流电压控制增益来提高系统的稳定性。文献[19]建立了张北柔直工程的换流器阻抗模型,得出电流内环将导致系统出现负阻尼,为此通过用电压单环策略代替电压电流双闭环控制重塑系统阻抗特性,消除了换流站的负阻尼,有效实现了系统稳定性提升。针对直流电压控制环参数变化如何影响弱网条件下VSC稳定性的内在机制,文献[20]联合阻抗分析法和特征值分析法研究了整流和逆变模式下直流电压环的动态特性对交流电流环的影响。结果表明,在整流模式下,直流电压控制环倾向于触发低频振荡;而在逆变模式下,它则更容易诱发高频振荡。进一步地,文献[21]通过频率和阻尼的变化定量评估了直流电压控制环和PLL的交互作用。结果表明,当二者的控制带宽相接近时,低频振荡模式的频率与阻尼特性趋向减小,高频振荡模式则与之相反。上述研究分析了采用跟网型控制方式的柔直系统的稳定性问题,该控制方式缺乏有效的电网支撑能力,容易受到电网电压波动的影响。随着新能源发电的大规模接入,电网中同步机占比的下降,电网强度的降低,跟网型控制方式在稳定性方面面临挑战[22]。与跟网型控制不同,构网型控制能显著降低变流器在弱电网下的振荡风险[23]。文献[24]通过探究构网型变流器的输出阻抗,指出其有功无功功率控制会使得其输出阻抗在低于工频的频率段呈现出负阻尼特性。文献[25]研究了构网型控制器的电压电流内环对小信号稳定性的影响规律,证明了前馈增益和线路参数主要影响高频振荡模态、低频振荡模态主要受下垂系数影响等结论。
上述文献大多局限于单一或特定控制方式,并未建立针对混合控制策略的分析架构;另一方面,现有研究主要通过功率加权平均法[26-28]或参数集中辨识法[29-30]将多个VSC等效为单一模型,忽略了不同控制策略给系统带来的差异化影响。本文研究的双VSC并联的多端柔直系统源于白鹤滩—江苏特高压混合级联直流输电工程[31],该工程采用了定直流电压控制与定功率控制并联的VSC结构。对于多端直流或多馈入直流,它们的拓扑结构仅在直流侧或交流侧存在单一的电气耦合,与本文系统交直流双侧均存在强耦合的特点存在较大差异。综上,当前研究无论是在换流器层面还是电气拓扑结构层面与本文的研究对象均存在差异,导致所得结论难以完全适用于白江特高压混合级联直流输电工程,无法充分解释振荡机理。
本文充分考虑实际工程特点,对双受端VSCHVDC系统进行建模与机理分析,旨在充分认知不同控制策略下系统的振荡特性,为实际工程稳定运行提供重要指导,主要贡献如下。
1) 分析了控制策略、非对称电网强度、联络线对系统稳定性的影响,形成了考虑联络线约束关系的SCR可行域,为系统的运行规划及参数的动态调整提供指导。
2) 在考虑电网拓扑变化等多种影响因素的情况下,构建双受端VSC-HVDC系统多种运行工况,通过数值仿真验证了所构建SCR可行域的有效性。
1 双受端VSC-HVDC系统结构及控制方式
本文依据功率平衡原理将双VSC并联的直流侧等效为受控电流源模型[32-33],通过两个受端换流器及相连的交流系统来反映白江工程中低端柔直系统的稳定特性。系统结构图如图1所示,其特点为:VSC1和VSC2在直流侧通过共同的直流母线相连,形成并联变流器结构,在交流侧通过公共耦合点(point of common coupling, PCC)分别馈入交流系统AC1和AC2,并且,AC1与AC2通过联络线Tie互联连接。其中,VSC1-HVDC采用定直流电压控制以支撑系统的直流母线电压,对应的变量用下标j=1表示;VSC2-HVDC采用定有功功率和无功功率控制以保证功率的稳定传输,对应的变量用下标j=2表示。
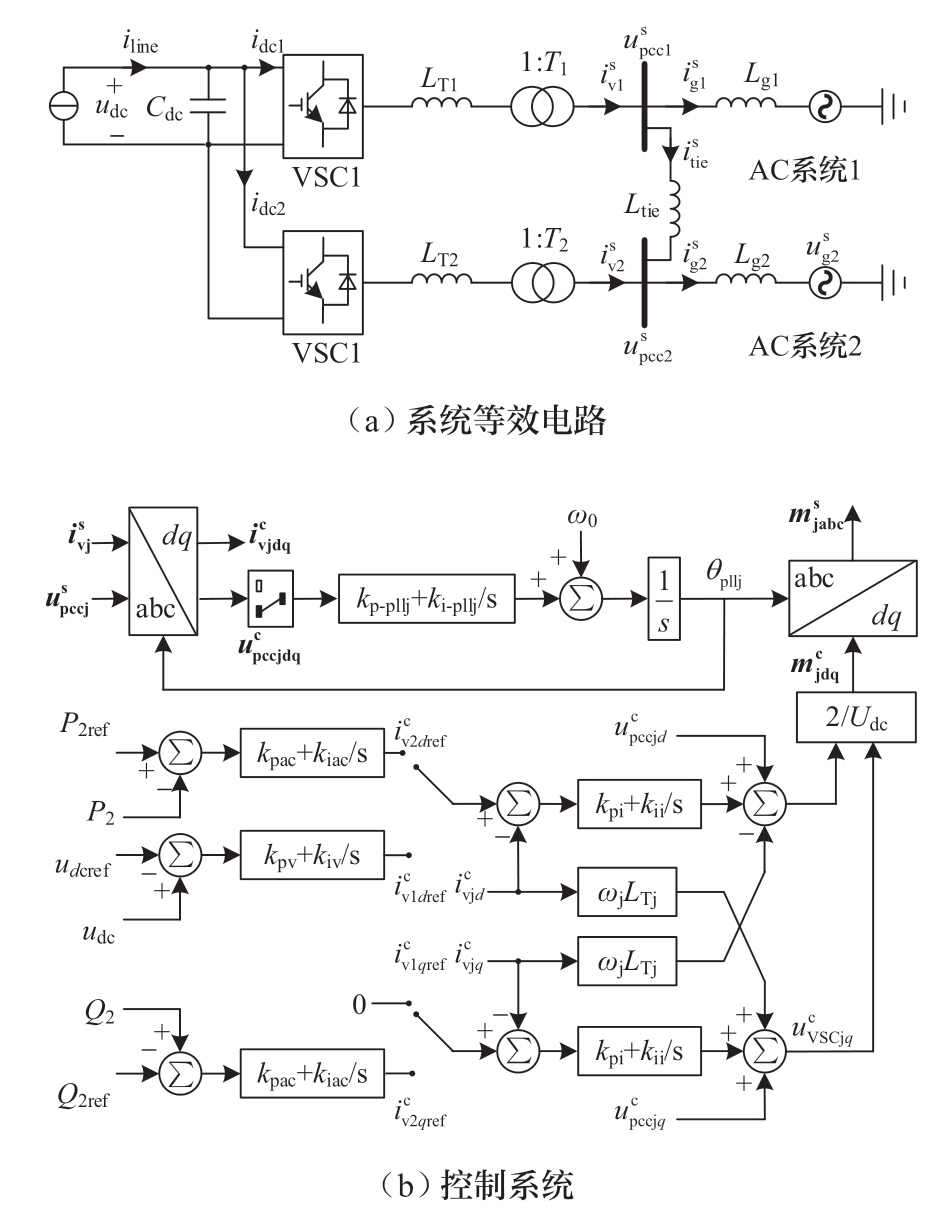
图1 双受端VSC-HVDC系统结构图
Fig.1 Structure of two-terminal VSC-HVDC system
图中,直流端口通过等效直流电容Cdc以实现对直流母线电压的稳定支撑,且Cdc=6C/Nph,C为子模块电容值,Nph为桥臂子模块数[32];交流端口通过换流变压器Tj与交流系统连接。uVSCj、idcj、ivj分别为换流器交流端口电压、直流电流、交流电流;uPCCj为PCC点电压;iline和udc分别为直流传输线电流和VSC直流侧电压。ugj、igj分别为交流系统的等值电动势和网侧电流;itie为联络线的电流;Lgj为交流系统的等值电感,表征了交流系统的电网强度;Ltie为联络线电感;LTj为换流变压器漏感。VSC1-HVDC和VSC2-HVDC的控制系统均采用电流矢量控制,前者的q轴电流参考值设定为0以保证无功功率为零,kpij和kiij分别为比例系数和积分系数;kpv和kiv分别为直流电压外环的比例系数和积分系数;kpac和kiac分别为功率外环的比例系数和积分系数。控制器的输出为dq坐标系的调制信号mjd和mjq,经过SPWM调制生成换流器的交流侧电压。PLL采用同步旋转坐标系锁相环(synchronous reference frame PLL,SRF-PLL),θpllj、ω0、ωj分别表示跟踪得到的相位、额定角频率、PLL的输出角频率;kp-pllj和ki-pllj分别为锁相环控制器的比例系数和积分系数。
本文中,下标abc表示三相静止坐标系变量,下标dq表示两相旋转坐标系变量,其中两相旋转坐标系包含与电网电压同步坐标系(用上标s表示) 和基于PLL的控制器坐标系(用上标cj表示)。大写形式和上标^分别表示表示变量对应的稳态值和小信号量,符号s和符号p分别表示拉普拉斯算子和微分算子。
2 双受端VSC-HVDC系统的小信号模型
2.1 系统动态方程
2.1.1 主电路动态方程
根据图1所示的双受端VSC-HVDC系统结构图,选择![]() 、
、![]() 、udc为状态变量,建立主电路的动态方程。VSC-HVDC交流端口到PCC点的KVL方程可以写为
、udc为状态变量,建立主电路的动态方程。VSC-HVDC交流端口到PCC点的KVL方程可以写为
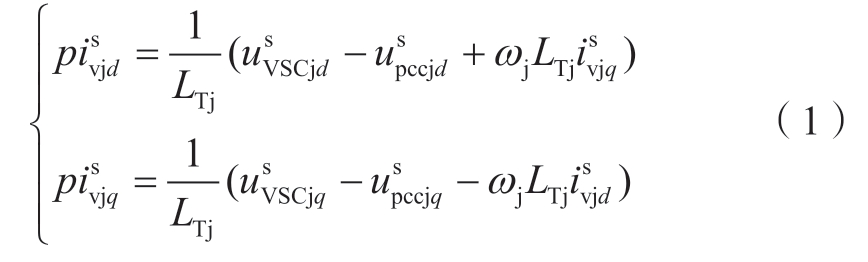
在abc坐标系下,联络线电流itie满足
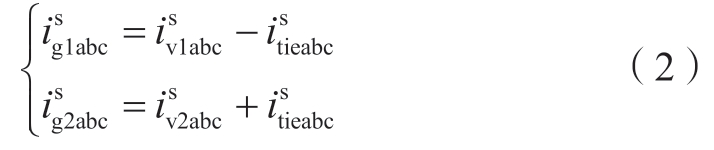
考虑到控制器位于dq旋转坐标系,基于θpll1对式(2)进行派克变换,可以获得联络线在dc1qc1坐标系下的动态方程
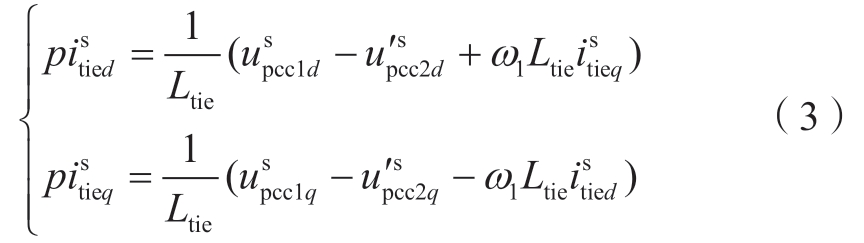
式中:![]() 为dc1qc1坐标系下的VSC2并网点电压。
为dc1qc1坐标系下的VSC2并网点电压。
为了便于统一建模,需利用式(4)将位于dc2qc2坐标系下VSC2的并网点电压![]() 折算至dc1qc1坐标系下,
折算至dc1qc1坐标系下,![]() 与
与![]() 满足[34]
满足[34]
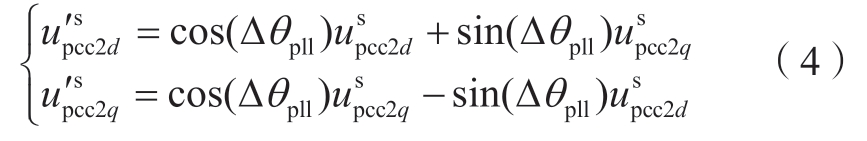
其中,∆θ pll = θpll1 -θpll2
基于上述分析,可得到PCC点到交流系统的KVL方程
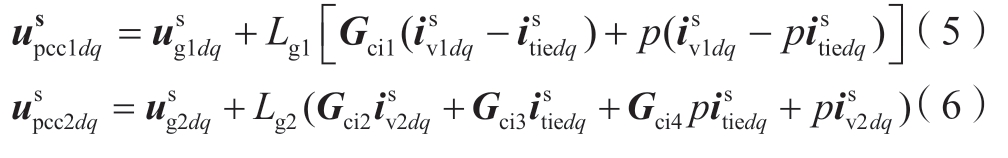
式中:
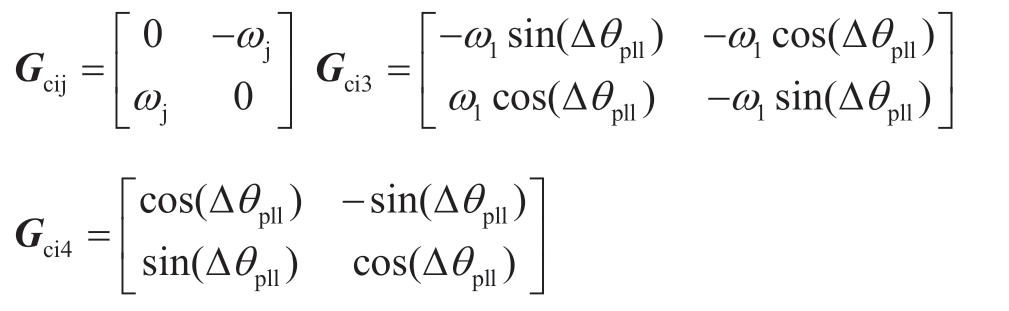
根据图1中VSC直流端口的KCL约束关系,可得到双受端VSC-HVDC系统直流端口的动态方程:
2.1.2 控制系统动态方程
对于VSC1-HVDC,将内外环PI环节的积分输出记作状态变量x1~x3,可得定直流电压控制器的动态方程:
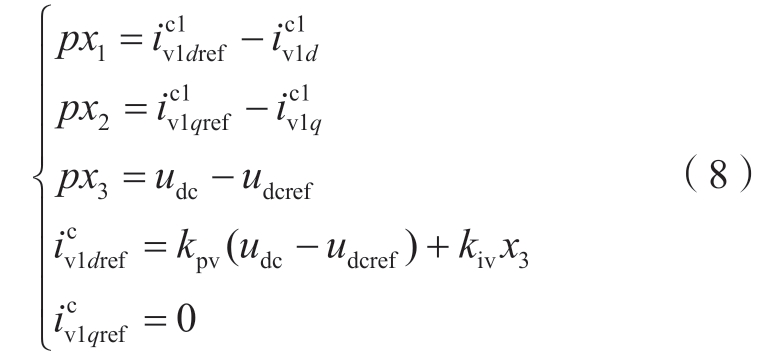
式中:udcref为直流母线电压的参考值。
同理可得VSC2-HVDC定功率控制系统的动态方程:
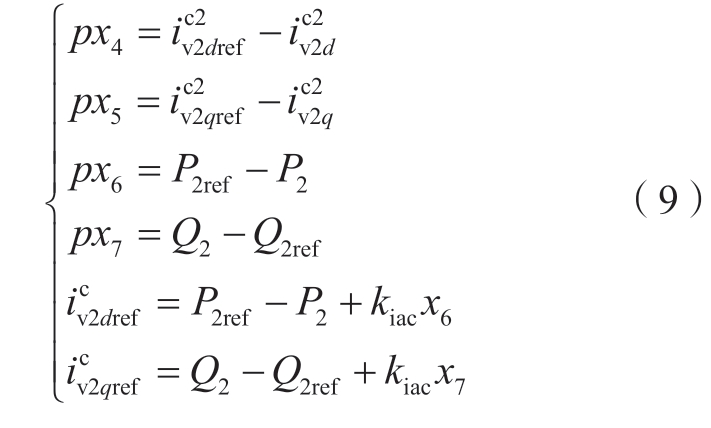
式中:Pref、Qref为VSC2-HVDC有功功率、无功功率的参考值。
2.1.3 PLL动态方程
根据图1,将PLL控制器PI环节积分输出记作状态变量xpllj,同时选取PLL跟踪得到的相位θpllj作为状态变量,可得到SRF-PLL的动态方程
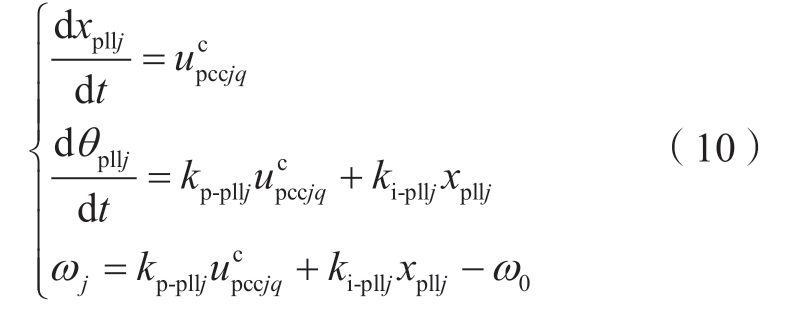
2.2 双受端VSC-HVDC系统闭环互联模型
依据双受端VSC-HVDC系统拓扑关系,组合上述主电路动态方程、控制系统动态方程、PLL动态方程并进行线性化可得到双受端VSC-HVDC系统的小信号模型,如式(11)所示。
式中:上述小信号模型的状态变量为
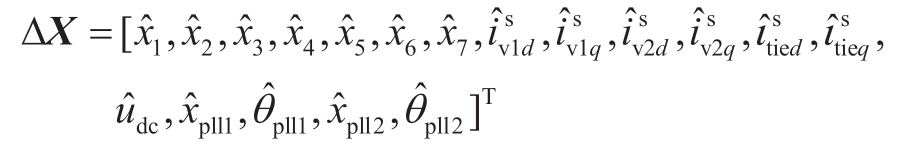
由于PCC点的电压会受交流系统阻抗的影响而存在波动,导致基于PLL得到的控制器坐标系dcjqcj和同步坐标系dsqs之间存在角度偏差[35]。计及上述偏差,可得到两种坐标系下PCC电压、VSC交流端口电流、调制信号的转换关系
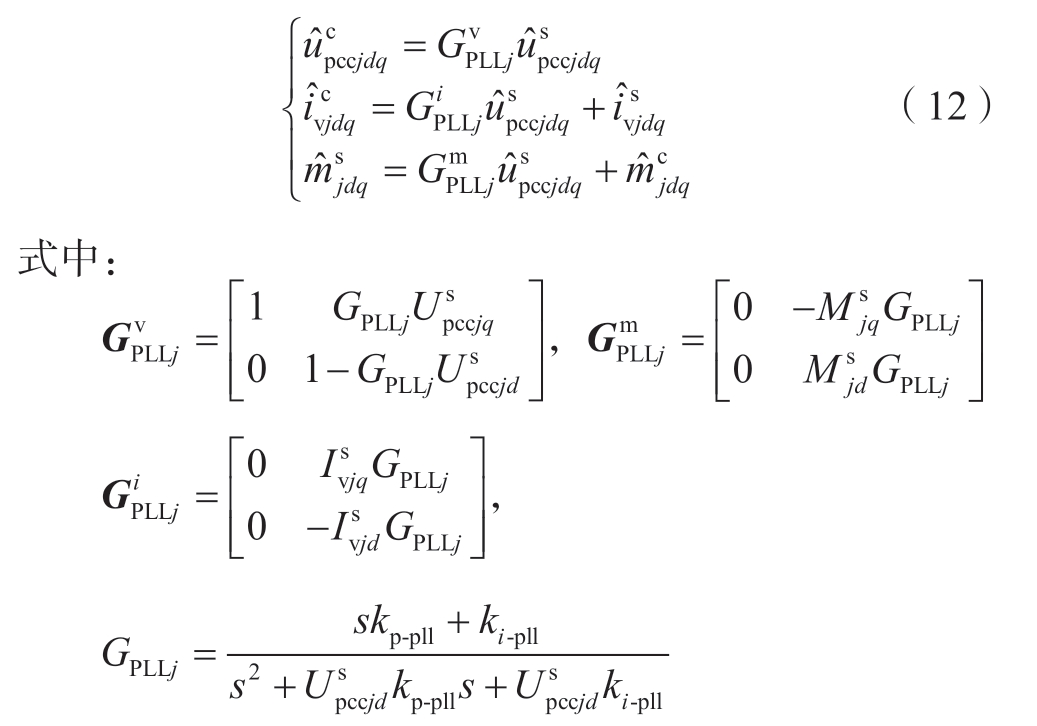
基于上述分析和所建立的小信号模型可获得双受端VSC-HVDC系统的闭环互联模型,如图2所示,该框图的构建过程详见附录A。
附录 A 双受端VSC-HVDC系统闭环互联模型构建过程
首先 定 义 如 下变 量:![]() ,表示PCC1和PCC2稳态相位差;
,表示PCC1和PCC2稳态相位差;![]() ,表示PCC1和PCC2相位小信号量组成的向量。
,表示PCC1和PCC2相位小信号量组成的向量。
对式(1)取小信号可得:
式中
将式(4)代入(3),并取小信号可得
式中
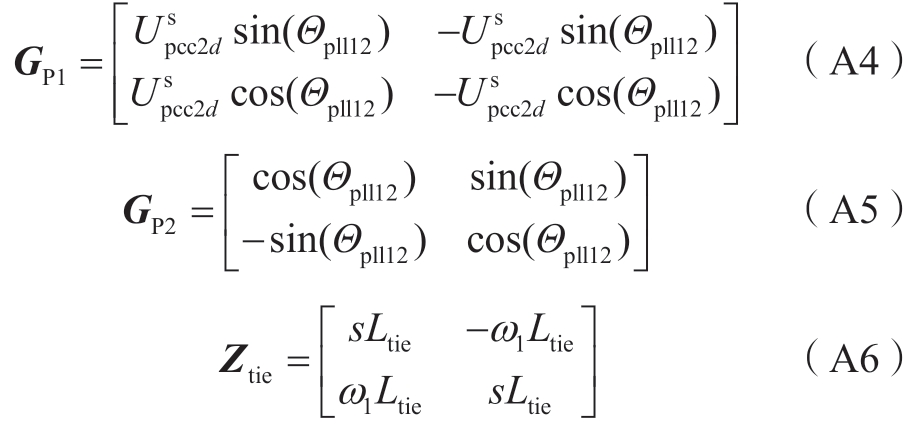
对式(5)、(6) 取小信号可得:
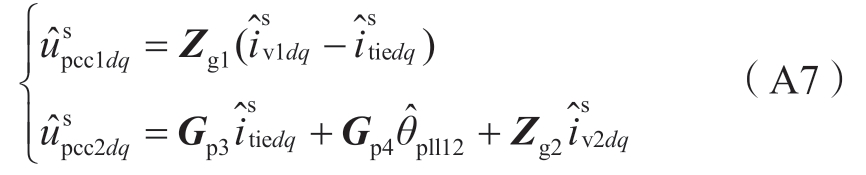
式中
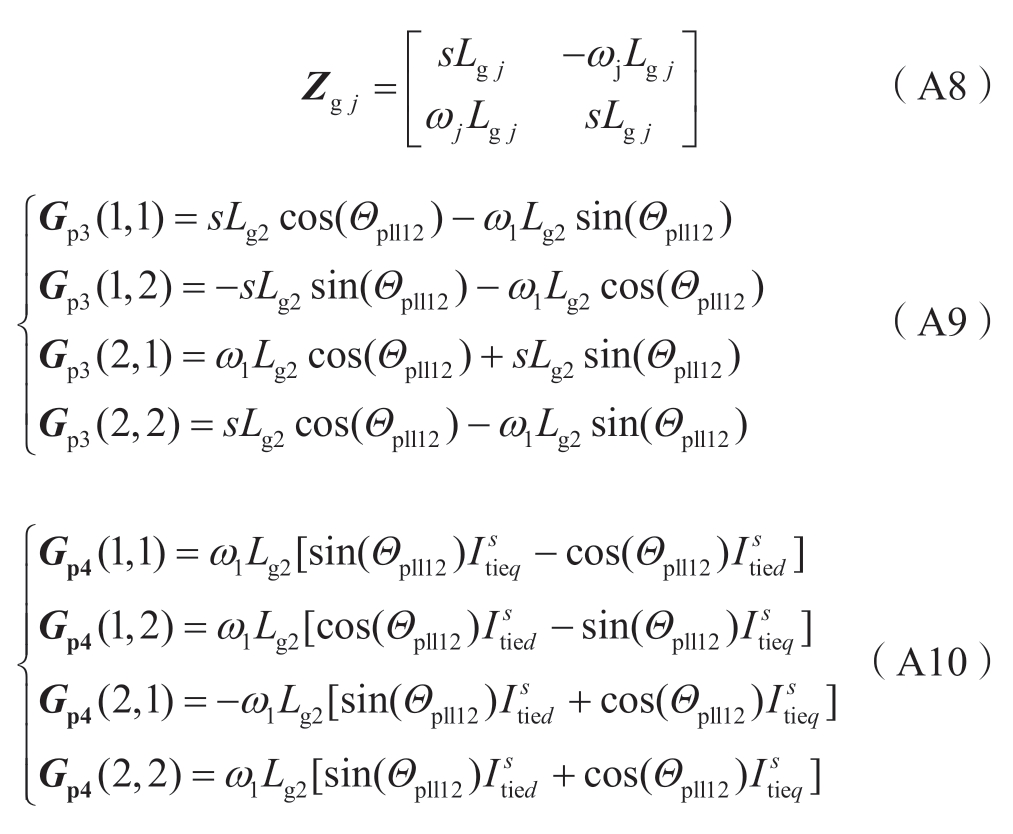
对式(7)取小信号可得:
VSC1和VSC2直流侧功率为:
若不计换流器的损耗,则VSC1 (VSC2) 交流侧功率和直流侧功率相等:
VSC交流侧电压与直流电压及调制信号的关系为
将式(A13)、(A14)代入式(A12)可得
对式 (A14)、(A15) 分别取小信号可得
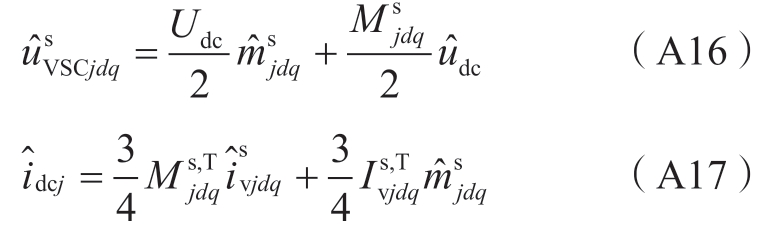
将式 (A17) 代入 (A11) 可得
整合式 (A1)—(A18) 即可构建双受端VSCHVDC系统的闭环互联模型。
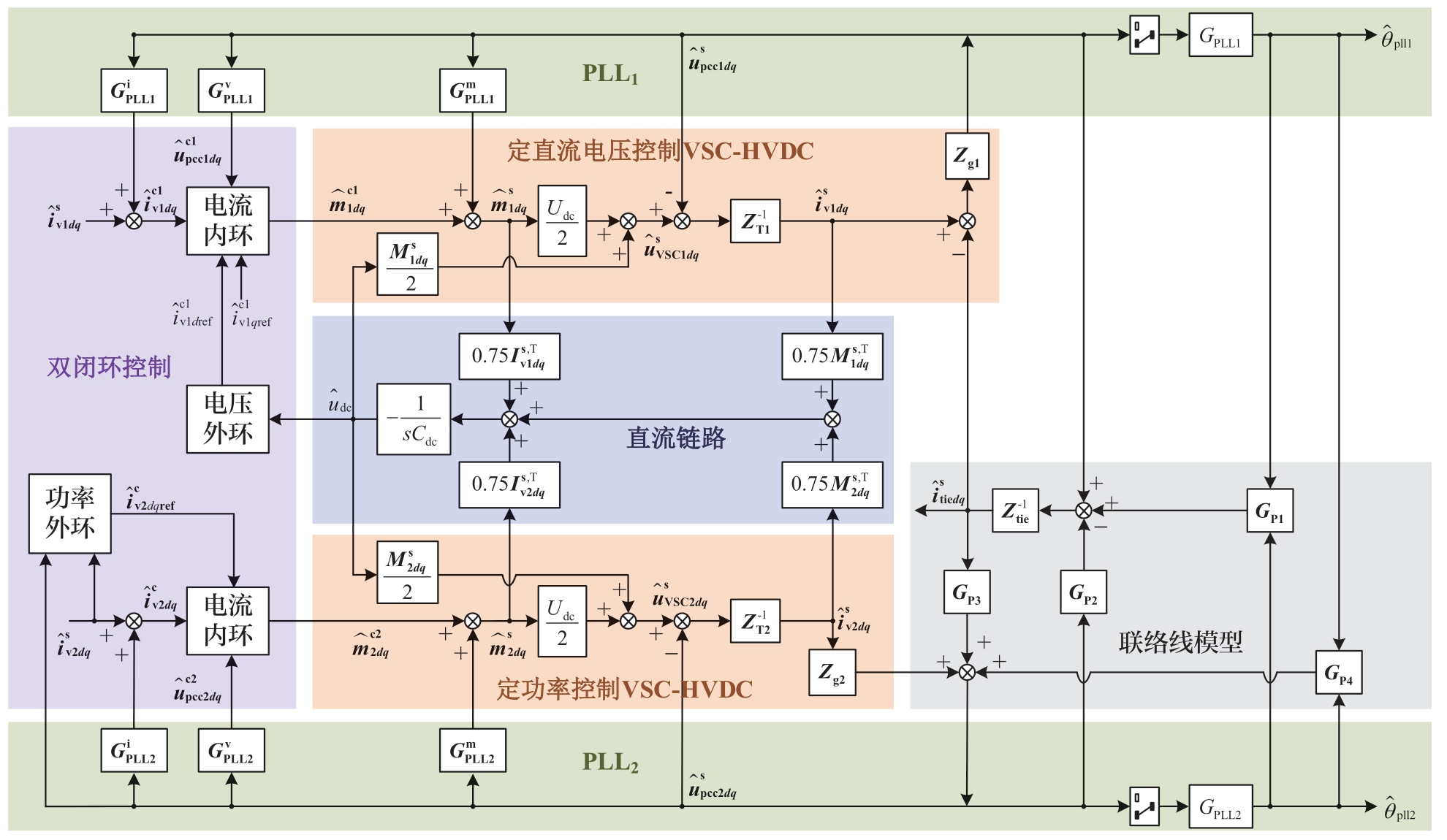
图2 双受端VSC-HVDC系统闭环互联模型
Fig.2 Closed-loop interconnection model of two-terminal VSC-HVDC system
根据图2所示的双受端VSC-HVDC系统闭环互联模型可知:①关于定直流电压控制VSC-HVDC和定功率控制VSC-HVDC(橙色背景):不同的外环控制策略展现出对调制信号差异化的调控能力,且该差异与直流电压、PLL将共同影响双受端VSC-HVDC系统的交流端口电压。②关于直流链路(蓝色背景):根据附录式 (A18) 可知,直流母线电压的动态响应特性与调制信号和换流器交流侧电流存在强动态交互作用,且该交互作用由系统的外环控制策略共同决定。此外,不同的控制策略会通过共同的直流链路产生耦合,从而导致系统运行过程中定直流电压控制系统与定功率控制系统将产生交互耦合作用。③关于PLL(绿色背景):结合式(12)可知,PLL1和PLL2动态特性主要影响换流器交流侧电流、调制信号以及PCC电压,且该影响机理又间接地受外环控制策略的调节。④关于联络线模型(灰色背景):PLL1和PLL2的相位信息会通过联络线与交流系统产生耦合,且耦合强度直接受联络线长度的影响。
综上,双受端VSC-HVDC系统是一个强交互动态系统,差异化的控制策略使得VSC1与VSC2表现出不同的运行特性。在此基础上,直流侧电容与交流联络线将VSC1与VSC2动态交互耦合,加剧了系统响应的复杂。导致了系统的稳定性不是由单独的一种控制策略所决定,而是定电压/定功率混合控制的共同影响,表现出与单一控制策略下的VSC-HVDC不同。
3 双受端VSC-HVDC系统小信号模型验证
第2章推导得到了图1所示的双受端VSC-HVDC系统的小信号模型,并根据图1在MATLAB/Simulink搭建了对应的电磁暂态模型,通过对比小信号模型和电磁暂态模型的计算结果,验证了小信号模型的准确性,系统参数如表1和表2所示。表中的短路比 (SCR) 定义如式(13)所示[36],其中UtiN (i=1, 2,…) 为交流母线i额定电压;PdciN为与交流母线i相连直流系统额定功率。
表1 主电路参数
Table 1 Main circuit parameters
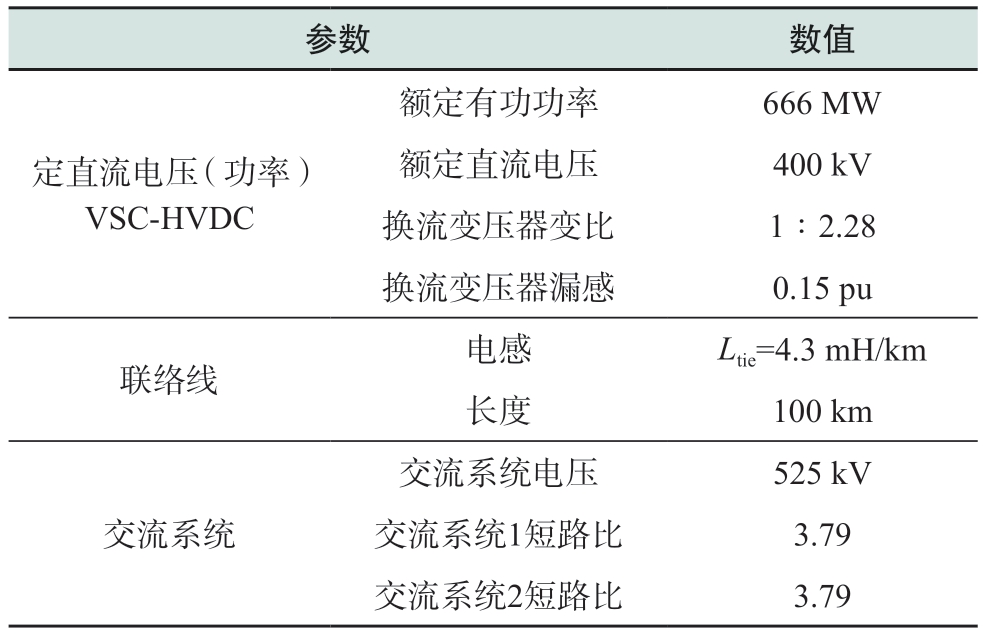
参数 数值定直流电压 (功率)VSC-HVDC额定有功功率 666 MW额定直流电压 400 kV换流变压器变比 1∶2.28换流变压器漏感 0.15 pu联络线 电感 Ltie=4.3 mH/km长度 100 km交流系统交流系统电压 525 kV交流系统1短路比 3.79交流系统2短路比 3.79
表2 控制系统参数
Table 2 Control system parameters
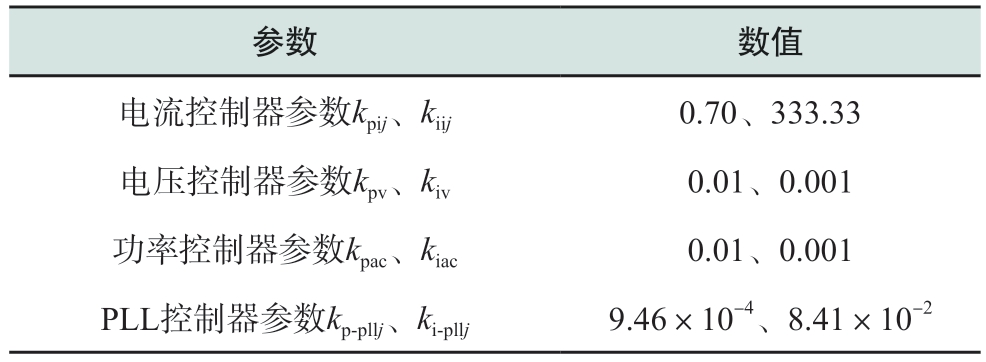
参数 数值电流控制器参数kpij、kiij 0.70、333.33电压控制器参数kpv、kiv 0.01、0.001功率控制器参数kpac、kiac 0.01、0.001 PLL控制器参数kp-pllj、ki-pllj 9.46×10-4、8.41×10-2
系统初始运行条件为:Pj = 1.0 pu,Upccj = 1.0 pu,SCRj = 3.79。图3和图4为小信号模型和电磁暂态模型仿真结果的对比,其中,实线波形为电磁暂态模型的仿真结果,虚线波形是小信号模型的理论计算结果。图3 (a) 为VSC1-HVDC的直流电压参考值udcref在t = 1 s时从1.0 pu阶跃到1.5 pu,t = 2 s时切换至1.25 pu过程中系统直流母线电压的波形;图3 (b) 为VSC1-HVDC的有功功率参考值P1ref在t = 1 s时从1.0 pu阶跃到0.5 pu,t = 2 s时切换至0.75 pu过程中VSC1的有功功率波形。图4 (a)—(d) 为VSC2-HVDC的有功功率参考值P2ref在t = 1 s时从1.0 pu阶跃到0.5 pu,t = 2 s时切换至0.75 pu过程中VSC2的有功功率、无功功率、d轴交流电流、A相交流电流的波形。
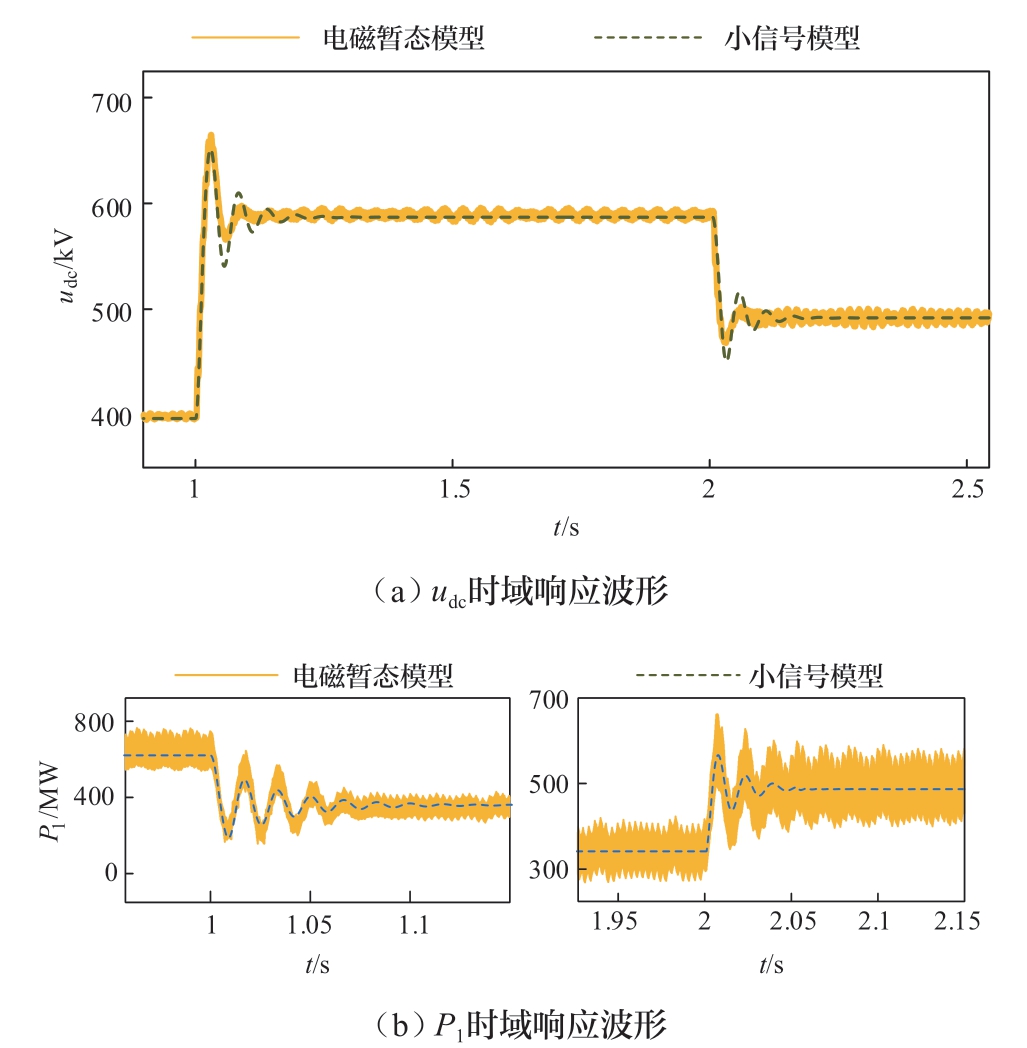
图3 udcref、P1ref阶跃时系统动态特性
Fig.3 System dynamic characteristics with step-change of udcref and P1ref
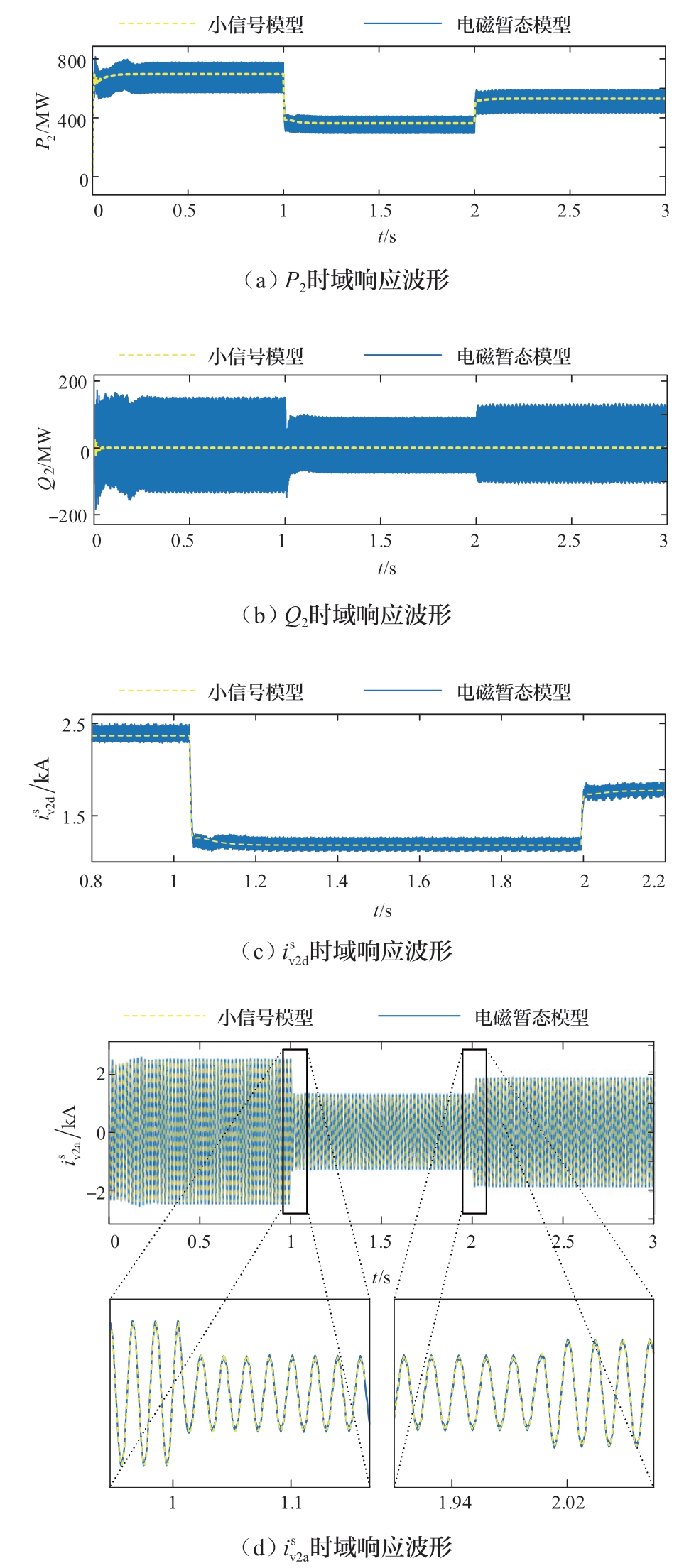
图4 P2ref阶跃时系统动态特性
Fig.4 System dynamic characteristics with step-change of P2ref
根据图3和图4可知,在不考虑电磁暂态模型的开关过程导致的额外高频分量的情况下,小信号模型和电磁暂态模型的时域相应模型基本重合,表明所建立的小信号模型能够准确反映双受端VSC-HVDC系统的动态特性。
4 双受端VSC-HVDC系统稳定性分析
本章基于建立的双受端VSC-HVDC系统小信号模型,结合特征值分析法,通过分析系统主导模态随参数的变化趋势,研究了交流系统强度与联络线长度对所研究系统稳定性的影响。
1)交流系统强度。
根据图1可知,双受端VSC-HVDC系统在交流侧经联络线并联,当系统所连交流电网强度较弱时,交流母线电压易受扰动影响,导致VSC1和VSC2之间的动态耦合增强,进而影响系统整体的稳定性[37],因此选取了3组短路比组合工况进行研究。
工况1:保持SCR2不变,改变SCR1由1变到4;工况2:保持SCR1不变,改变SCR2由4变到1;工况3:同时改变SCR1和SCR2由4变到1。上述3种工况下的联络线长度均为100 km,控制器参数如表2所示,得到双受端VSC-HVDC系统的根轨迹如图5(a)、(b)所示。
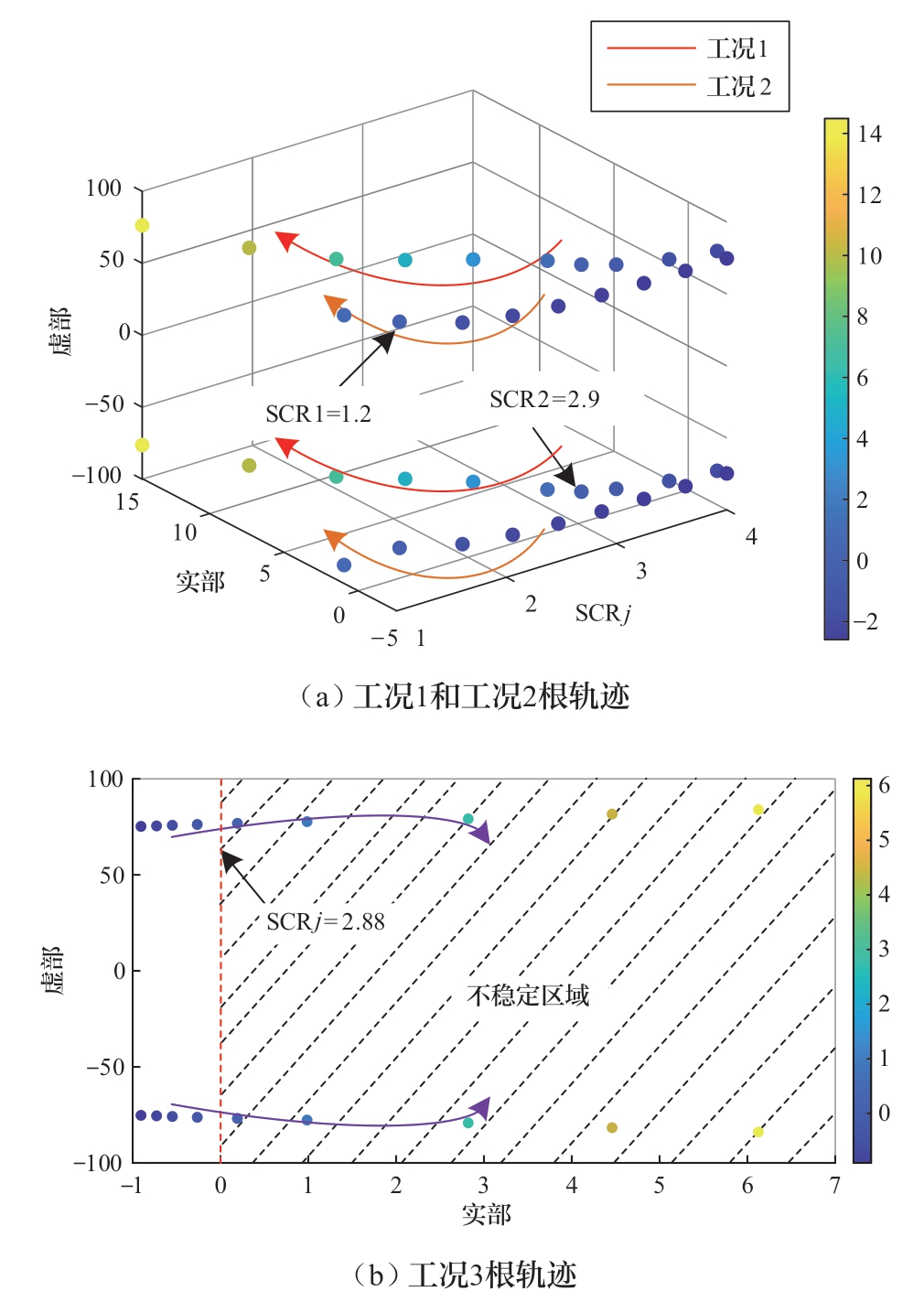
图5 不同短路比工况下系统的根轨迹
Fig.5 Root loci of system under different SCR settings(tie line length = 100 km)
由图5(a) 可知,工况1中,随着SCR2减小,主导模态逐渐靠近虚轴,系统稳定裕度逐渐减小,当SCR2 < 2.9时,系统发生失稳现象。同理,工况2中,在SCR1减小的过程中,系统稳定性逐渐减小,当SCR1 < 1.2时,系统振荡失稳。根据上述分析可知,尽管工况1和工况2在设置方式上展现出相同的变化趋势,但由于VSC1-HVDC和VSC2-HVDC采用不同的控制方式,交流系统1的最小可接受SCR相比交流系统2更低。因此当电气部分参数一致时,采用定直流电压控制的VSC-HVDC受电网强度的影响较小,能够在额定功率相同的情况下接受强度更弱的交流系统。根据图5 (b),随着SCR1和SCR2同时减小,系统的小信号稳定性也减弱,当SCRj小于2.88时,系统发生失稳现象。
进一步地,基于图5设置更多的短路比组合工况,获取系统SCR可行域如图6所示,图中由两条约束关系构成的黑色实线为短路比临界线,表示当SCR1或者SCR2发生变化时可接受的最小SCR,如临界线上的点A、B、C分别对应于工况1、工况2、工况3的最小可接受SCR,黑色实线上方和下方的区域分别表示SCR的可行域和不可行区域。
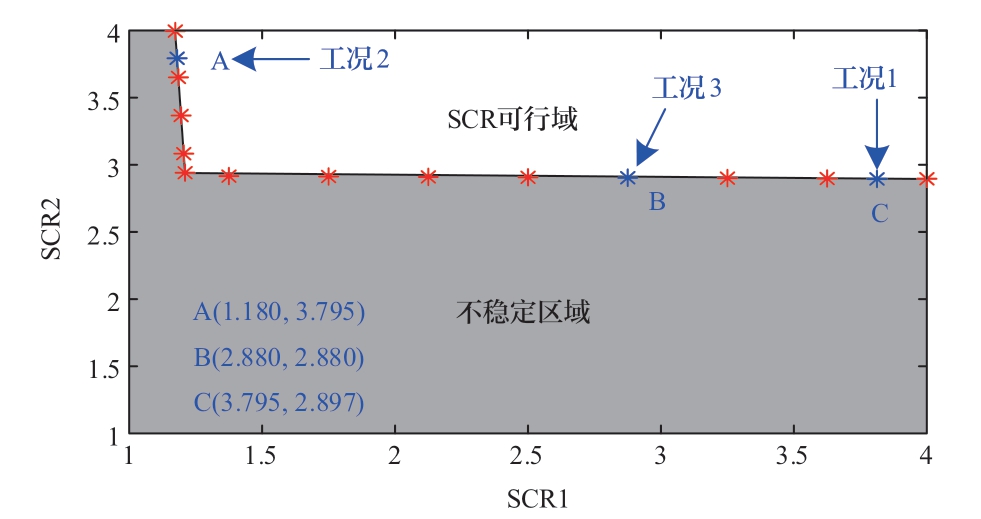
图6 SCR的可行域
Fig.6 Feasible region of SCR (tie line length = 100 km)
2)联络线长度。
如图1所示的双受端VSC-HVDC的交流侧系统通过交流联络线相连,同时结合图2可知,不同联络线长度对差异化控制策略的动态响应耦合程度和二者电气量的交互程度的影响显著不同[38]。为此,选择如下3种短路比组合工况对上述影响做进一步评估:工况A:SCR1 = 3.79,SCR2 = 2.9;工况B:SCR1 = 2.9,SCR2 = 3.79;工况C:SCR1 = 2.9,SCR2 = 2.9。3种工况下的联络线长度从1 km到200 km变化,得到双受端VSC-HVDC系统的根轨迹如图7(a)—(c)所示,图中的颜色栏与主导模态的实部相对应。
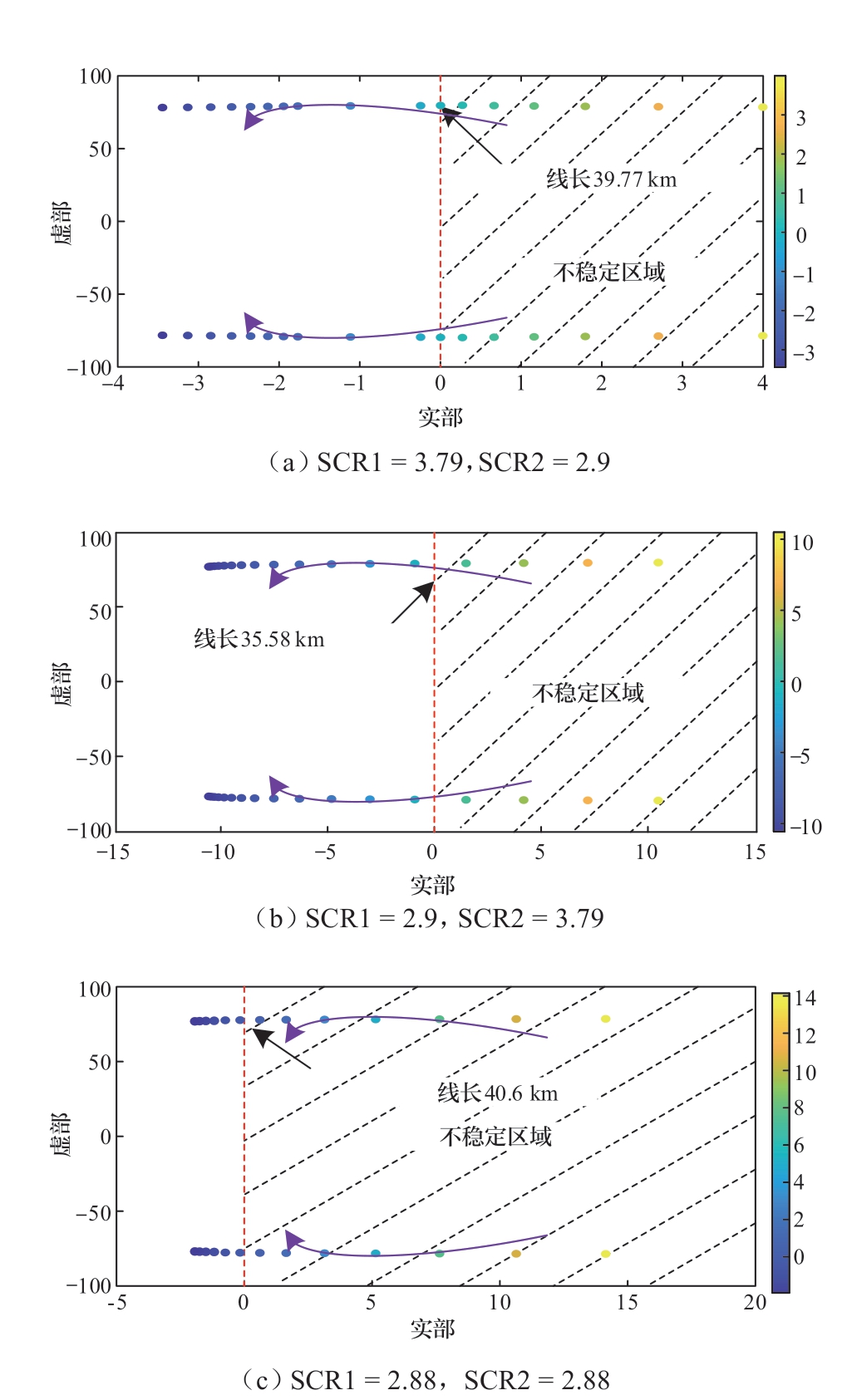
图7 不同短路比工况下联络线长度变化时系统的根轨迹
Fig.7 Root loci of system under different SCR settings with tie line length varying
根据图7(a)—(c)可得到:联络线长度减少会影响系统的稳定性,这是因为联络线长度的减小将缩短了VSC1-HVDC和VSC2-HVDC之间的电气距离,加剧双受端VSC-HVDC的交互程度,使得两系统对扰动的共同作用更为敏感。当联络线长度小于最小可接受值时,系统将无法保障正常稳定运行,例如工况A和工况B的最小可接受联络线长度分别为39.77 km和35.58 km。尽管两种工况在设置方式上展现出相同的变化趋势,但二者的最小可接受联络线长度不同,根据前文分析可知,VSC2-HVDC受电网强度影响较大,因此交流系统2强度较弱时,则需要更长的联络线以保证系统的稳定性。同理由图7 (c)可知,SCR1和SCR2均为2.9时,联络线长度小于40.6 km会导致系统发生失稳。
进一步地,绘制不同联络线长度下的SCR可行域如图8所示,其中SCR可行域的定义方式与图6相同,从图中可以看出,随着联络线长度增加,VSC1和VSC2的交互作用逐渐减弱,系统SCR临界线向左下方移动,SCR可行域增大,系统的稳定性逐渐增强。
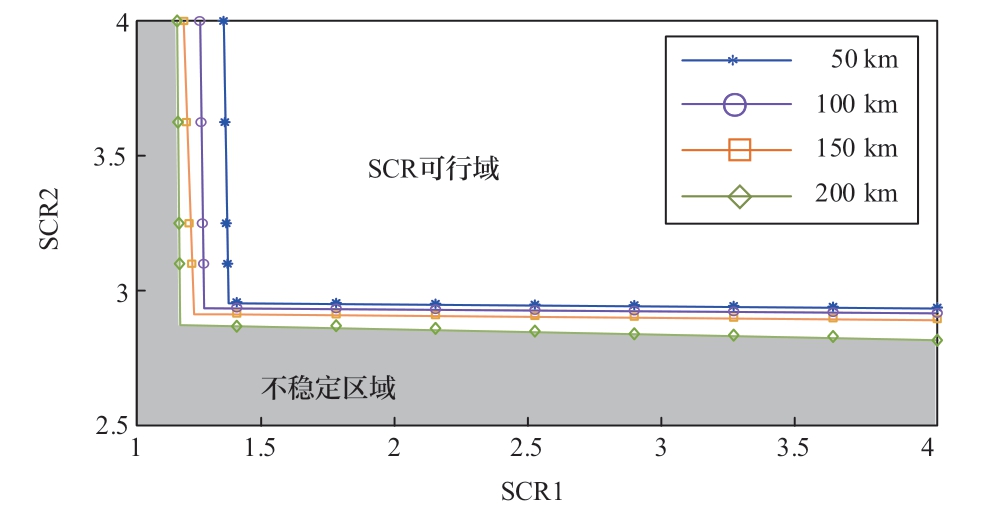
图8 不同联络线长度下的SCR可行域
Fig.8 Feasible region of SCR with different tie line length
在MATLAB/Simulink搭建双受端VSC-HVDC系统仿真模型,系统在稳定参数(Pj=1.0 pu,SCR1 = 2.0,SCR2 = 3.0,联络线长度100 km)下启动后,保持其他参数不变,将SCR1先后切换为1.3、1.1,对VSC1-HVDC的直流母线电压、功率、并网点电流和并网点电压波形进行绘制,如图9所示。
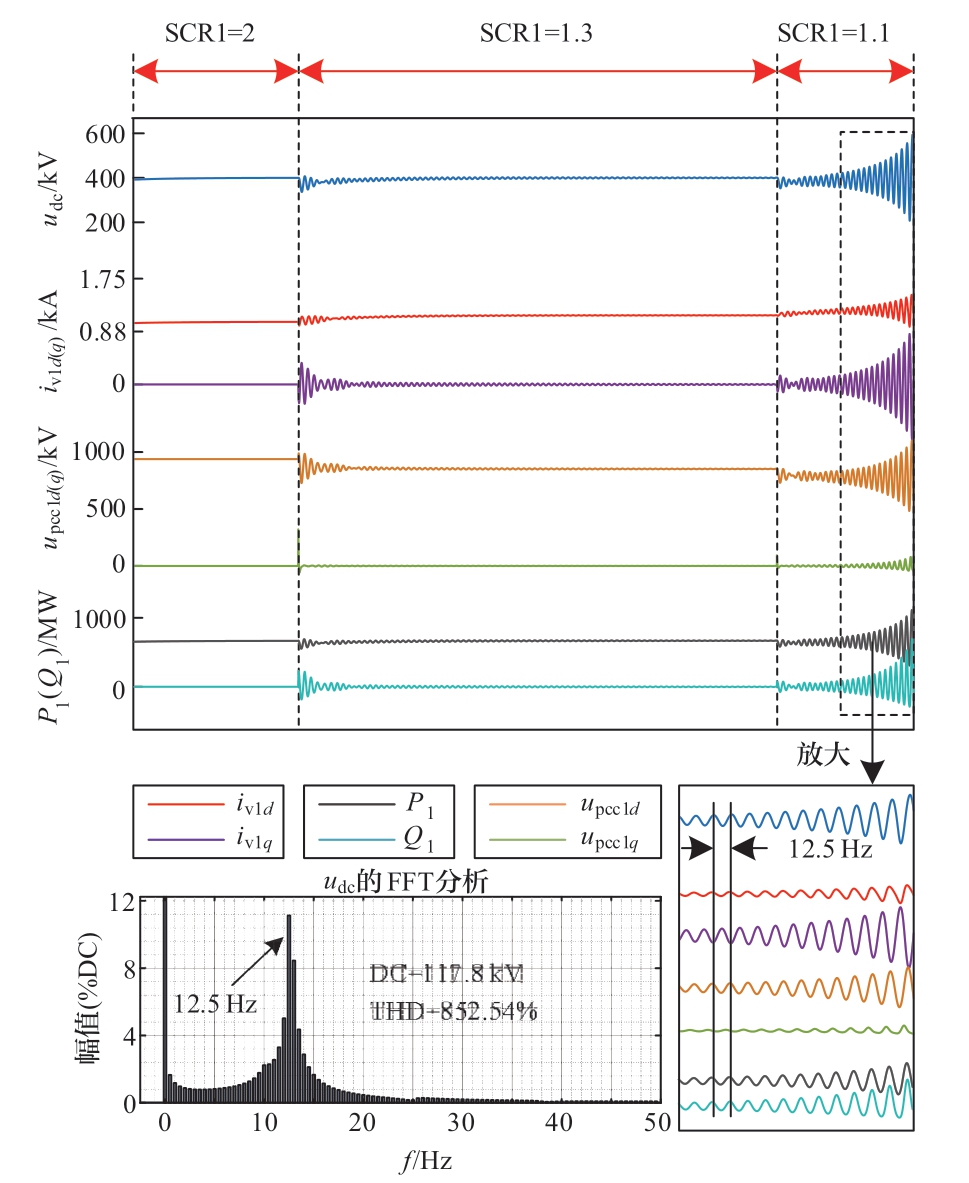
图9 SCR可行域验证结果
Fig.9 Validation results of Feasible region for SCR
根据图9可知,系统在SCR1切换为1.3后虽产生小幅振荡,但由于此时的SCR1和SCR2位于可行域内,振荡被迅速抑制,各参数能够良好收敛到稳态值;当SCR1切换为1.1时,系统逐渐失稳,且振荡无法被抑制。对振荡过程中的直流母线电压udc等波形进行FFT分析,其存在12.5 Hz的振荡分量。
图10为联络线长度切换前后系统的时域波形,系统在稳定参数(SCR1 = 1.3°,SCR2 = 3.625,联络线长度100 km)下启动后,保持其他参数不变,将联络线长度切换为50 km。根据图10可知,联络线长度切换后,系统运行点从可行域突变到不稳定区域,系统逐渐失稳。根据图9和图10可知,本文针对双受端VSC-HVDC系统所开展的稳定性研究能够与仿真良好对应,从而能够为系统关键参数选择提供理论指导。
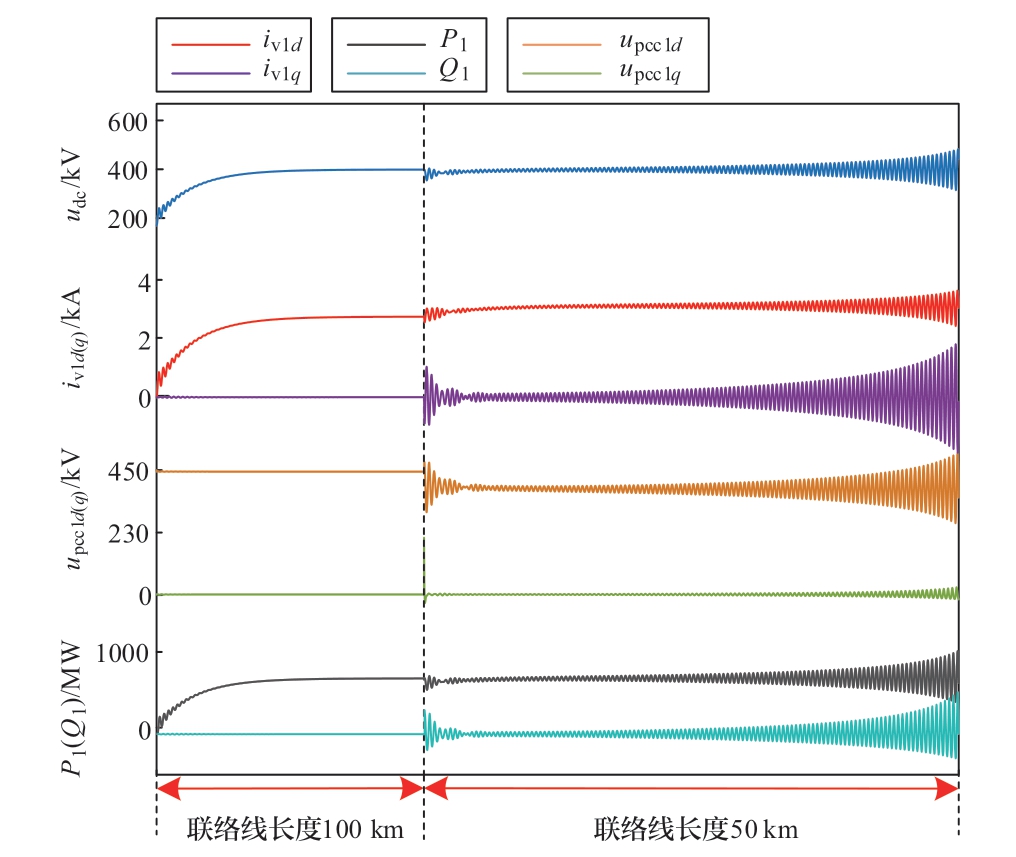
图10 联络线长度改变时系统动态特性
Fig.10 System dynamic characteristics with tie line length varying
5 结论
本文考虑了不同控制外环、直流链路的耦合、PLL动态等因素,建立了双受端VSC-HVDC系统的小信号模型,通过对比其和MATLAB/Simulink电磁暂态模型的时域响应,验证了所建立模型的准确性。应用特征值分析法,评估了交流系统强度和联络线长度对系统稳定性的影响,所得结论如下。
1)当主电路参数一致时,与采用定功率控制的VSC-HVDC相比,采用定直流电压控制的VSC-HVDC受电网强度的影响较小,能够在额定功率相同的情况下联接强度更弱的交流系统。
2)通过建立定直流电压和定功率运行的VSC与交流系统SCR的约束关系,分析了混合控制方式下双受端VSC-HVDC系统的SCR可行域。结果表明,定直流电压控制的VSC-HVDC,能够稳定运行在更小的短路比工况。此外,联络线长度对系统稳定性影响方面,与定直流电压控制相比,定功率运行的VSCHVDC对于联络线长度的变化更敏感,因此,系统AC1与系统AC2耦合作用较强时,不利于定功率模式下的VSC-HVDC稳定运行。
参考文献
-
[1]
刘欣,袁易,王利桐,等.柔性直流输电系统三端口混合参数建模及其稳定性分析[J].电工技术学报,2024,39(16):4968-4984.LIU Xin, YUAN Yi, WANG Litong, et al.Three-port hybrid parameter modeling and stability analysis of MMC-HVDC system[J].Transactions of China Electrotechnical Society,2024, 39(16): 4968-4984(in Chinese). [百度学术]
-
[2]
姜惠兰,肖瑞.提高系统暂态稳定性的VSC-HVDC有功无功联合附加控制策略[J].电力自动化设备,2024,44(8):138-144.JIANG Huilan, XIAO Rui.Combined active and reactive additional control strategy of VSC-HVDC for improving system transient stability[J].Electric Power Automation Equipment, 2024, 44(8): 138-144(in Chinese). [百度学术]
-
[3]
饶宏,周月宾,李巍巍,等.柔性直流输电技术的工程应用和发展展望[J].电力系统自动化,2023,47(1):1-11.RAO Hong, ZHOU Yuebin, LI Weiwei, et al.Engineering application and development prospect of VSC-HVDC transmission technology[J].Automation of Electric Power Systems, 2023, 47(1): 1-11(in Chinese). [百度学术]
-
[4]
韩璐,尹纯亚,戴晨,等.高比例新能源送端系统暂态电压运行风险分析[J].电力系统保护与控制,2024,52(1):23-34.HAN Lu, YIN Chunya, DAI Chen, et al.Transient voltage operational risk of a high-proportion new energy sending system[J].Power System Protection and Control, 2024, 52(1):23-34 (in Chinese). [百度学术]
-
[5]
杜文娟,郝向坤,陈珏.光伏场经柔直并网振荡稳定性分析与抑制方法研究[J].电力工程技术,2024,43(3):2-11.DU Wenjuan, HAO Xiangkun, CHEN Jue.Oscillation stability analysis and mitigation method of photovoltaic field connected to the grid via VSC-HVDC[J].Jiangsu Electrical Engineering,2024, 43(3): 2-11 (in Chinese). [百度学术]
-
[6]
尹聪琦,谢小荣,刘辉,等.柔性直流输电系统振荡现象分析与控制方法综述[J].电网技术,2018,42(4):1117-1123.YIN Congqi, XIE Xiaorong, LIU Hui, et al.Analysis and control of the oscillation phenomenon in VSC-HVDC transmission system[J].Power System Technology, 2018,42(4): 1117-1123(in Chinese). [百度学术]
-
[7]
魏伟,许树楷,李岩,等.南澳多端柔性直流输电示范工程系统调试[J].南方电网技术,2015,9(1):73-77.WEI Wei, XU Shukai, LI Yan, et al.The system commissioning of Nan’ao VSC-MTDC demonstration project[J].Southern Power System Technology, 2015, 9(1):73-77(in Chinese). [百度学术]
-
[8]
张鑫宇,薛峰,李碧君,等.双馈风场串补系统次同步振荡紧急控制策略[J].电力工程技术,2023,42(5):108-116.ZHANG Xinyu, XUE Feng, LI Bijun, et al.Emergency control strategy for subsynchronous oscillation of DFIG-based wind farms with a series-compensated line[J].Electric Power Engineering Technology, 2023, 42(5): 108-116(in Chinese). [百度学术]
-
[9]
黄润鸿,朱喆,陈俊,等.南澳多端柔性直流输电工程高压直流断路器本体故障控制保护策略研究及验证[J].电网技术,2018,42(7):2339-2345.HUANG Runhong, ZHU Zhe, CHEN Jun, et al.Research and experimental validation of control and protection strategy of HVDC circuit breaker in fault condition application in Nan’ao multi-terminal VSC-HVDC system[J].Power System Technology, 2018, 42(7): 2339-2345(in Chinese). [百度学术]
-
[10]
SAAD H, FILLION Y, DESCHANVRES S, et al.On resonances and harmonics in HVDC-MMC station connected to AC grid[J].IEEE Transactions on Power Delivery, 2017,32(3): 1565-1573. [百度学术]
-
[11]
郭贤珊,刘泽洪,李云丰,等.柔性直流输电系统高频振荡特性分析及抑制策略研究[J].中国电机工程学报,2020,40(1):19-29.GUO Xianshan, LIU Zehong, LI Yunfeng, et al.Characteristic analysis of high-frequency resonance of flexible high voltage direct current and research on its damping control strategy[J].Proceedings of the CSEE, 2020, 40(1): 19-29(in Chinese). [百度学术]
-
[12]
LYU J, CAI X, AMIN M, et al.Sub-synchronous oscillation mechanism and its suppression in MMC-based HVDC connected wind farms[J].IET Generation, Transmission &Distribution, 2018, 12(4): 1021-1029. [百度学术]
-
[13]
姜崇学,马秀达,邹强,等.柔性直流输电系统的高频谐波保护方法与工程实践[J].电力系统自动化,2024,48(3):150-158.JIANG Chongxue, MA Xiuda, ZOU Qiang, et al.Highfrequency harmonic protection methods and engineering practice for flexible DC transmission systems[J].Automation of Electric Power Systems, 2024, 48(3): 150-158(in Chinese). [百度学术]
-
[14]
郑少明,刘一民,董鹏,等.张北工程风电柔直汇集系统次、超同步振荡分析[J].全球能源互联网,2023,6(6):608-617.ZHENG Shaoming, LIU Yimin, DONG Peng, et al.Analysis of sub/super-synchronous oscillation between wind farm and MMC in Zhangbei Project[J].Journal of Global Energy Interconnection, 2023, 6(6): 608-617(in Chinese). [百度学术]
-
[15]
HE Y J, XIANG W, NI B Y, et al.Impact of strength and proximity of receiving AC systems on cascaded LCC-MMC hybrid HVDC system[J].IEEE Transactions on Power Delivery, 2022, 37(2): 880-892. [百度学术]
-
[16]
王潇,刘辉,邓晓洋,等.双馈风电场经柔性直流并网系统的宽频带振荡机理分析与风险评估[J].全球能源互联网,2020,3(3):238-247.WANG Xiao, LIU Hui, DENG Xiaoyang, et al.Mechanism analysis and risk assessment of broadband resonance in doublyfed induction generator-based wind farms integration through flexible HVDC[J].Journal of Global Energy Interconnection,2020, 3(3): 238-247(in Chinese). [百度学术]
-
[17]
MORRIS J F, AHMED K H, EGEA-ÀLVAREZ A.Analysis of controller bandwidth interactions for vector-controlled VSC connected to very weak AC grids[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7343-7354. [百度学术]
-
[18]
HUANG Y H, YUAN X M, HU J B, et al.DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 445-458. [百度学术]
-
[19]
马秀达,文继锋,严伟,等.张北柔性直流工程电压单环控制策略应用分析[J].电力系统自动化,2025,49(2):198-207.MA Xiuda, WEN Jifeng, YAN Wei, et al.Application analysis of single-loop voltage control strategy in Zhangbei flexible DC project of China[J].Automation of Electric Power Systems,2025, 49(2): 198-207(in Chinese). [百度学术]
-
[20]
LU D P, WANG X F, BLAABJERG F.Impedance-based analysis of DC-link voltage dynamics in voltage-source converters[J].IEEE Transactions on Power Electronics, 2019,34(4): 3973-3985. [百度学术]
-
[21]
WANG D, LIANG L, SHI L, et al.Analysis of modal resonance between PLL and DC-link voltage control in weakgrid tied VSCs[J].IEEE Transactions on Power Systems, 2019,34(2): 1127-1138. [百度学术]
-
[22]
DU W, CHEN Z, SCHNEIDER K P, et al.A comparative study of two widely used grid-forming droop controls on microgrid small-signal stability[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 963-975. [百度学术]
-
[23]
马秀达,卢宇,田杰,等.柔性直流输电系统的构网型控制关键技术与挑战[J].电力系统自动化,2023,47(3):1-11.MA Xiuda, LU Yu, TIAN Jie, et al.Key technologies and challenges of grid-forming control for flexible DC transmission system[J].Automation of Electric Power Systems, 2023, 47(3):1-11(in Chinese). [百度学术]
-
[24]
LI G X, CHEN Y D, LUO A, et al.Analysis and mitigation of subsynchronous resonance in series-compensated gridconnected system controlled by a virtual synchronous generator[J].IEEE Transactions on Power Electronics, 2020,35(10): 11096-11107. [百度学术]
-
[25]
EBERLEIN S, RUDION K.Impact of inner control loops on small-signal stability and model-order reduction of gridforming converters[J].IEEE Transactions on Smart Grid, 2022,14(4): 2812-2824. [百度学术]
-
[26]
ZHOU Y H, ZHAO L, LEE W J.Robustness analysis of dynamic equivalent model of DFIG wind farm for stability study[C]//2018 IEEE/IAS 54th Industrial and Commercial Power Systems Technical Conference (I&CPS).May 7-10,2018, Niagara Falls, ON, Canada.IEEE, 2018: 1-9. [百度学术]
-
[27]
ALI M, ILIE I S, MILANOVIC J V, et al.Wind farm model aggregation using probabilistic clustering[J].IEEE Transactions on Power Systems, 2013, 28(1): 309-316. [百度学术]
-
[28]
HUANG L B, XIN H H, LI Z Y, et al.Identification of generalized short-circuit ratio for on-line stability monitoring of wind farms[J].IEEE Transactions on Power Systems, 2020,35(4): 3282-3285. [百度学术]
-
[29]
李悦蕾,张放,申洪明,等.基于同步相量频谱拟合的电力系统次/超同步振荡的动态参数辨识[J].中国电机工程学报,2025,45(2):551-565.LI Yuelei, ZHANG Fang, SHEN Hongming, et al.Dynamic parameter identification with synchronous spectrum fitting technique for sub/supersynchronous oscillations in power systems[J].Proceedings of the CSEE, 2025, 45(2): 551-565(in Chinese). [百度学术]
-
[30]
张放,刘军,李佳欣,等.基于同步相量轨迹拟合的电力系统次同步/超同步振荡的实时参数辨识[J].中国电机工程学报,2023,43(4):1413-1426.ZHANG Fang, LIU Jun, LI Jiaxin, et al.Real-time parameter identification of subsynchronous/supersynchronous oscillation in power system based on synchronous phasor trajectory fitting[J].Proceedings of the CSEE, 2023, 43(4): 1413-1426(in Chinese). [百度学术]
-
[31]
郭春义,吴张曦,赵成勇.特高压混合级联直流输电系统中多MMC换流器间不平衡电流的均衡控制策略[J].中国电机工程学报,2020,40(20):6653-6663.GUO Chunyi, WU Zhangxi, ZHAO Chengyong.Balancing control strategy for unbalanced current between multiple MMC converts in hybrid cascaded UHVDC system[J].Proceedings of the CSEE, 2020, 40(20): 6653-6663(in Chinese). [百度学术]
-
[32]
李云丰,汤广福,庞辉,等.直流电网电压控制器的参数计算方法[J].中国电机工程学报,2016,36(22):6111-6121.LI Yunfeng, TANG Guangfu, PANG Hui, et al.Controller parameters calculating method of DC voltage loop for DC grid[J], Proceedings of the CSEE, 2016, 36(22): 6111-6121. [百度学术]
-
[33]
李云丰,汤广福,贺之渊,等.MMC型直流输电系统阻尼控制策略研究[J].中国电机工程学报,2016,36(20):5492-5503.LI Yunfeng, TANG Guangfu, HE Zhiyuan, et al.Damping control strategy research for MMC based HVDC system[J].Proceedings of the CSEE, 2016, 36(20): 5492-5503(in Chinese). [百度学术]
-
[34]
刘炜,郭春义,赵成勇.混合双馈入直流输电控制系统交互影响机理分析[J].中国电机工程学报,2019,39(13):3757-3766.LIU Wei, GUO Chunyi, ZHAO Chengyong.Mechanism analysis of control interactions in dual-infeed hybrid HVDC system[J].Proceedings of the CSEE, 2019, 39(13): 3757-3766(in Chinese). [百度学术]
-
[35]
王垚鑫,李萌,年珩,等.基于VSC的功率双向交直流互联系统直流侧阻抗特性分析及重塑[J].中国电机工程学报,2024,44(19):7660-7671.WANG Yaoxin, LI Meng, NIAN Heng, et al.Analysis and reshaping of DC-side impedance characteristic in VSCsbased bidirectional power AC/DC interconnected system[J].Proceedings of the CSEE, 2024, 44(19): 7660-7671(in Chinese). [百度学术]
-
[36]
林伟芳,汤涌,卜广全.多馈入交直流系统短路比的定义和应用[J].中国电机工程学报,2008,28(31):1-8.LIN Weifang, TANG Yong, BU Guangquan.Definition and application of short circuit ratio for multi-infeed AC/DC power systems[J].Proceedings of the CSEE, 2008, 28(31): 1-8(in Chinese). [百度学术]
-
[37]
邵冰冰,赵书强,高本锋,等.连接弱交流电网的VSCHVDC失稳机理及判据研究[J].电工技术学报,2019,34(18):3884-3896.SHAO Bingbing, ZHAO Shuqiang, GAO Benfeng, et al.Instability mechanism and criterion analysis of VSC-HVDC connected to the weak AC power grid[J].Transactions of China Electrotechnical Society, 2019, 34(18): 3884-3896(in Chinese). [百度学术]
-
[38]
赵薇,郭春义,杨硕.混合级联直流输电系统整流/逆变不同控制回路动态交互作用与稳定性研究[J].中国电机工程学报,2024,44(1):231-244.ZHAO Wei, GUO Chunyi, YANG Shuo.Research on dynamic interaction and stability of rectifier/inverter control loop in hybrid cascade HVDC system[J].Proceedings of the CSEE,2024, 44(1): 231-244(in Chinese). [百度学术]
基金项目
国网江苏省电力有限公司科技项目资助(J2023144)。
Science and Technology Foundation of SGCC (J2023144).

