相关论文:
-

-
全球能源互联网
第8卷 第6期 2025年11月;页码:702-712
基于广义阻抗的新能源柔直送出系统小干扰稳定性评估与提升
Evaluation and Improvement of Small Disturbance Stability for Renewables VSC-HVDC Delivery System Based on Generalized Impedance
- 广东电网有限责任公司电力调度控制中心,广东省 广州市 510180
- ZHU Yu, WU Shuangxi, LU Qiuyu*, YANG Yinguo (Electric Power Dispatching Control Center of Guangdong Grid Co., Ltd., Guangzhou 510180, Guangdong Province, China
关键词
Keywords
摘 要
Abstract
目前,新能源柔性直流送出系统成为新型电力系统的典型形态之一,然而新能源变流器与柔直送端换流站动态交互复杂,系统振荡失稳时有发生。为此,聚焦新能源变流器锁相环主导的次同步振荡问题,提出了基于广义阻抗的系统小干扰稳定性评估与提升方法。首先,在全局极坐标系下建立了系统的频域模型,构造了等效的单输入单输出模型,提出了适用于新能源柔直送出场景的广义阻抗判据;其次,分析了锁相环与柔直送端换流站外环控制参数对于系统小干扰稳定性的影响;最后,提出了基于锁相环相位校正的稳定性提升方法,并通过仿真验证了方法有效性。提出的稳定性评估与提升方法可为新能源柔直送出系统的失稳风险评估与振荡抑制提供参考。
Currently, the renewables delivery system with voltage source converter-based high voltage direct current (VSCHVDC) has become one of the typical forms of new power systems.However, the interaction between renewable converters and the sending-end converter stations of VSC-HVDC is complicated, and system oscillation occurs from time to time.To address this issue, this paper focuses on the sub-synchronous oscillations dominated by the phase-locked loop of renewable converters and proposes a small disturbance stability assessment and enhancement method based on generalized impedance.Firstly, the frequency domain model of the system under the global polar coordinate is established, and an equivalent singleinput single-output model is constructed, and a generalized impedance criterion suitable for renewables VSC-HVDC delivery system is derived.Secondly, the impact of phaselocked loop and the outer-loop control parameters of the VSCHVDC sending-end converter station on the small disturbance stability is analyzed.Finally, a stability enhancement method based on phase correction of the phase-locked loop is proposed and the effectiveness of the proposed method is verified through simulations.This paper provides a reference for assessing and mitigating instability risks and oscillations in renewables VSCHVDC delivery system.
0 引言
随着“双碳”目标的提出,中国新能源装机容量逐年提高[1]。大规模新能源基地能够充分发挥区域风能、光能等自然条件优势,方便集约化调度管理。目前新能源基地采用柔性直流实现远距离、大容量并网[2-3],新能源柔直送出系统成为新型电力系统的典型形态之一,实际应用场景有海上风电送出、光伏柔直送出等[4]。然而,新能源柔直送出系统中柔直送端换流站与新能源变流器动态交互特性复杂,宽频振荡时有发生。例如南澳多端柔直工程曾发生30 Hz左右的次同步振荡[5-6],张北柔直工程在试验阶段也观察到次/超同步振荡现象[7];福建厦门柔直工程送端功率增大时电流波形出现25 Hz左右的振荡现象[8];德国北海海上风电场出现过300 Hz左右的中频振荡[9];舟山五端柔直发生几千Hz的高频振荡[10],为新型电力系统安全稳定运行带来挑战。
上述宽频振荡事故表明送出系统存在小干扰失稳风险。目前,小干扰稳定性分析主要通过特征值法或阻抗分析法,根据分析结果研究稳定性提升方法,从而抑制振荡。
文献[11]通过特征值法解析了风电场与柔直送端换流站之间的多频段振荡模态,并分析了次同步振荡模态的主导因素。文献[12]利用特征值法分析了送出系统的特征值轨迹,并评估了各个状态变量在不同振荡模态的参与程度。然而特征值法需要获取系统各个元件的详细参数以及控制结构等信息,即需要“白箱”模型,实际应用中难以实现,并且计算量往往较大,小干扰稳定性评估过程较为繁琐。
阻抗分析法可以利用“黑箱”模型进行分析,能够揭示新能源柔直送出系统小干扰失稳机理。例如针对送出系统的中高频段振荡问题,文献[13]对各个影响因素进行了灵敏度计算并提出了参数协同优化策略,从而抑制了系统中的高频谐波,实现了稳定性提升。文献[14]通过序阻抗模型分析了风电输出功率对系统稳定性的影响并提出了参数优化思路。另外序阻抗分析法也被应用于柔直送端换流站与新能源的中频段振荡机理分析[15]。文献[15]通过在柔直送端换流站添加虚拟阻抗以提高系统在中频段的稳定性,然而该研究忽略了交流电网线路阻抗的动态。文献[16]通过阻抗法分析了风电场功率增加对系统稳定性的影响,但未揭示风电场与柔直的交互机理。另外,由于交流侧阻抗为2×2矩阵,系统特征方程为多输入多输出模型(multiple input multiple output,MIMO),上述阻抗分析法均将MIMO模型降阶为单输入单输出(single input single output,SISO)模型,从而利用奈奎斯特曲线进行稳定性判断然而没有对提出的稳定性判据进行适用性讨论,其稳定性判据的开环传递函数无法保证在复平面右半平面不存在极点,因而需要结合开环传递函数极点分布与奈奎斯特曲线包围 (-1, j0) 点的圈数进行小干扰稳定性判断,导致阻抗分析法失去简洁快捷的优势,无法保证稳定判据表征的稳定裕度具备有效性。
广义阻抗法通过在极坐标下建立变流器和电网的阻抗模型,化解了阻抗矩阵中的耦合项,实现了特征方程的降阶,从而可准确判断锁相环(phase-locked loop,PLL)主导的次同步振荡风险,并且具有足够的稳定裕度的效果,即满足稳定性等价和标称性[17-18],因此该方法广泛运用于新能源并网系统的稳定分析中。然而与一般的新能源并网系统相比,新能源经柔直送出系统中存在新能源与交流电网、柔直系统三者之间的动态耦合关系,其失稳特征更加复杂,广义阻抗法在此场景中的适用性仍需进一步讨论。
针对新能源经柔直送出系统的小扰动稳定性分析问题,现有研究多基于阻抗模型构建广义阻抗并将系统稳定性问题等效为 SISO系统的判据分析,但尚未充分阐明不同阻抗判据的适用范围及其机理解释的一致性。为此,本文从广义阻抗与复电路视角出发,进一步探讨广义阻抗判据在柔直送出系统中的适用性,并分析系统振荡机理及锁相环对稳定性的影响。
本文其他章节内容如下:首先,在全局极坐标系下建立了送出系统的频域模型,并利用Schur补构造了等效单输入单输出(single input single output,SISO)模型,利用奈奎斯特曲线与伯德图判断系统稳定性,进一步分析了所提的广义阻抗稳定性判据的适用性;其次,基于稳定性判据,研究了锁相环主导的系统失稳机理,分析了锁相环与柔直送端换流站外环控制对于小干扰稳定性的影响,并提出了基于锁相环相位校正的稳定性提升方法;最后,通过仿真验证了基于广义阻抗的稳定性评估和提升方法的有效性。
1 新能源柔直送出系统频域建模
典型的新能源柔直送出系统的结构如图1所示,新能源场站采用单机聚合模型表示,等效为单台变流器(voltage source converter,VSC),发出功率由交流线路汇集至直流输电系统送出。为简化分析,基于下述条件将新能源柔直送出系统简化为图2所示的“标称”系统。
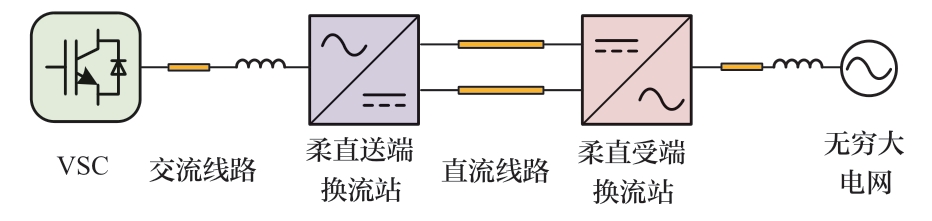
图1 典型新能源柔直送出系统示意图
Fig.1 Diagram of typical renewables VSC-HVDC delivery system
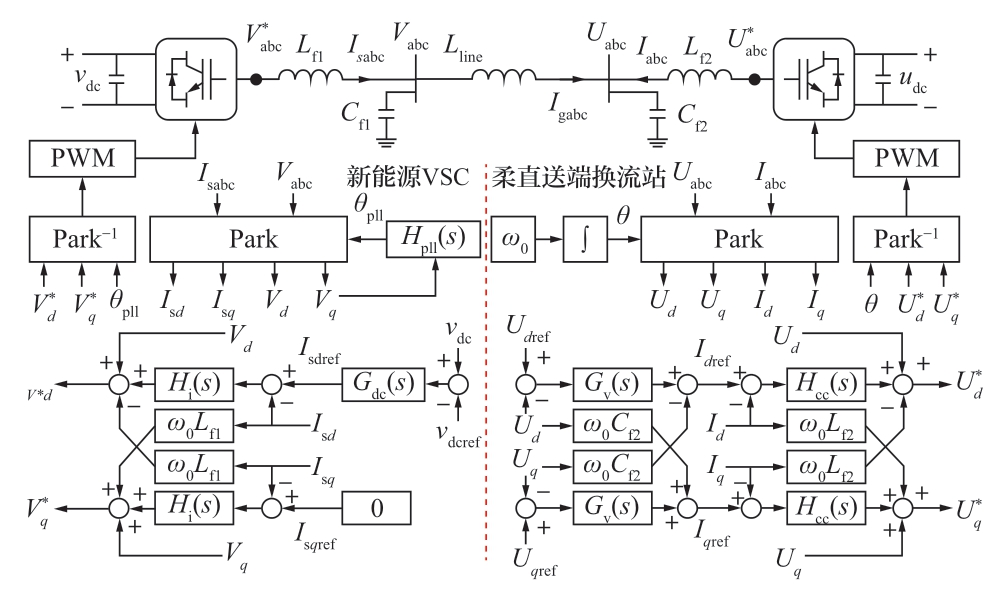
图2 新能源柔直送出标称系统
Fig.2 Diagram of simplified renewables VSC-HVDC delivery system
1) 新能源VSC和柔直换流站都采用典型的双环矢量控制。考虑新能源变流器设备中大部分光伏发电、直驱风机的外环控制策略为直流电压控制,并采用锁相环与柔直送端换流站坐标系进行同步。柔直送端换流站采用V/F控制结构[19]:电压外环为定交流电压控制,维持柔直并网点电压恒定,为新能源场站并网提供电压支撑;柔直换流站坐标系旋转频率固定为工频。详细控制结构参考图2。
2) 新能源机侧动态以及VSC外环动态响应较慢,在本文关注的次同步频段内可以忽略[20],即电流内环的电流参考值[Isdref, Isqref]T近似恒定。另外,由于滤波电容动态主要与高频振荡模态有关,对于本文关注的次同步振荡模态影响较小[21],因此本文忽略了新能源VSC侧的滤波电容动态,认为[ΔIgx, ΔIgy]T = [ΔIsx,ΔIsy]T。并且新能源VSC运行于单位功率因数。
3) 由于送端交流系统模态与直流侧模态、受端交流系统模态之间相互解耦,并考虑受端换流站能够维持直流线路电压维持恒定,即送端换流站的直流电压udc恒定[22]。并且,本文主要关注新能源VSC与柔直送端换流站之间的动态交互而非柔直送端换流站内部谐波动态,因此采用两电平对柔直送端环流进行建模。
4) 交流线路感性占优,忽略线路的电阻,这在35 kV以上的电压等级近似成立。
图2中Vabc为新能源VSC的公共耦合点三相电压;Uabc为柔直送端换流站公共耦合点三相电压;Isabc为流出新能源VSC的三相电流;Igabc为流经交流线路的三相电流;Iabc为流出柔直换流站的三相电流;Lfi,Cfi(i=1, 2)分别为新能源VSC与柔直送端换流站的LC滤波电感与电容;Hi(s)为新能源VSC内环PI控制传递函数;Hpll(s)为VSC锁相环PI控制传递函数;Gdc(s)为VSC直流电压外环PI控制传递函数;Hcc(s)为柔直送端换流站内环PI控制传递函数;Gv(s)为柔直送端换流站定交流电压外环PI控制传递函数;Lline为线路电感;vdc与udc分别为VSC与柔直送端换流站的直流电压。图2中Vdq为新能源VSC的公共耦合点dq坐标下电压。
下面利用极坐标系下的广义阻抗分析新能源柔直送出系统受扰后的动态过程,分别对交流线路、新能源VSC、柔直送端换流站进行阻抗建模。
1.1 交流线路频域模型
交流线路以及变压器采用电感等效模型,其中变压器电感折算到交流线路电感Lline中,在全局直角坐标系下的阻抗模型为

式中:[ΔIgx, ΔIgy]T为全局同步旋转坐标系下线路电流的x轴与y轴分量的微增量构成的列向量;[ΔVx, ΔVy]T为全局同步旋转坐标系下新能源VSC的并网点电压的x轴与y轴分量的微增量构成的列向量;[ΔUx, ΔUy]T为全局同步旋转坐标系下柔直送端换流站并网点电压的x轴与y轴分量的微增量构成的列向量;s为拉普拉斯算子。
然后将式 (1) 从全局直角坐标系变换到全局极坐标系下,为方便分析,全局直角坐标系的x轴与新能源VSC并网点电压x轴对齐,而柔直送端换流站并网点电压稳态相量与全局x轴存在相角差θU,那么极坐标系下的形式为
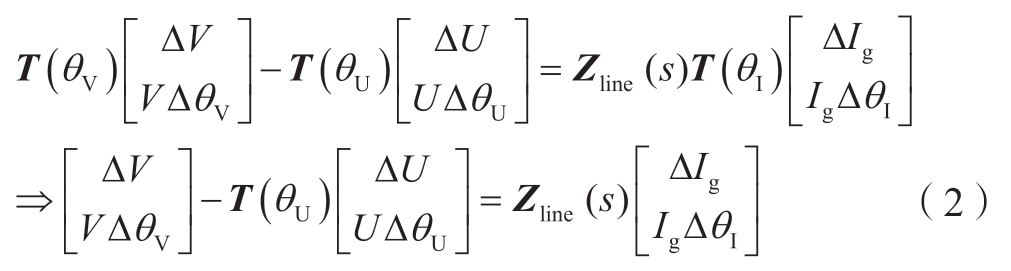
式中:V、U、Ig、θV、θU、θI分别为新能源VSC、柔直送端换流站以及线路电流相量稳态幅值与相角;Zline(s)为电网侧阻抗;T为坐标系变换矩阵,![]() ;Δ表示微增量。由前文假设条件2可知新能源VSC与线路电流相量稳态相角均为0,因此坐标系变换矩阵为单位阵。
;Δ表示微增量。由前文假设条件2可知新能源VSC与线路电流相量稳态相角均为0,因此坐标系变换矩阵为单位阵。
1.2 新能源VSC频域模型
对于单位功率因数的新能源VSC端口动态模型,目前频域阻抗建模已有较多成果,例如文献[23]给出了全局极坐标系下的导纳形式,本文直接引用该导纳形式如下。
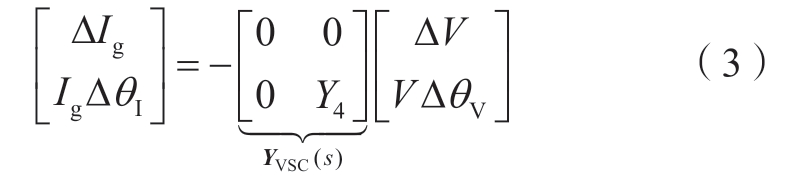
式中:![]() ;I0为新能源VSC出口电流幅值的稳态工作点;V0为VSC并网点电压幅值的稳态工作点。为了表达的简便性,后文省略传递函数的“(s)”。
;I0为新能源VSC出口电流幅值的稳态工作点;V0为VSC并网点电压幅值的稳态工作点。为了表达的简便性,后文省略传递函数的“(s)”。
1.3 柔直送端换流站频域模型
柔直送端换流站的阻抗模型可以根据动态方程求得,文献[24]推导了柔性送端直流换流站在全局直角坐标系下的导纳矩阵如式(4)所示。
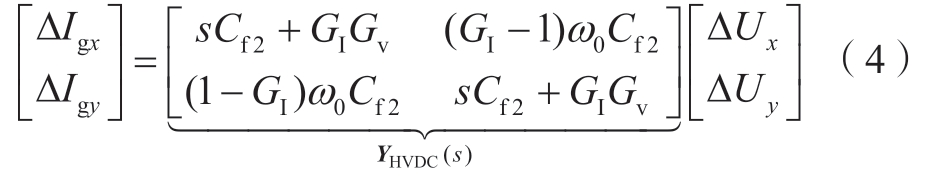
式中: Cf 2为线路电感;![]() ;
;![]() ;Hcc为电流内环PI控制器的传递函数;fVF为电压前馈滤波器的传递函数。
;Hcc为电流内环PI控制器的传递函数;fVF为电压前馈滤波器的传递函数。
式 (4) 的形式表明柔直送端换流站的导纳矩阵是具有特殊形式的对角阵:非对角元素互为相反数并且对角元素相等。
类似于式(2)的坐标变换过程,式 (4) 在极坐标系下的形式为
2 新能源柔直送出系统稳定性评估
第1章建立了送出系统的频域模型,本章首先推导送出系统的闭环特征方程;其次利用Schur补将系统MIMO模型降阶为SISO模型,进而得到了送出系统广义阻抗判据;最后讨论了广义阻抗判据的适用性,即稳定性判据是否满足标称性。
2.1 广义阻抗稳定性判据
联立式(2)—(3)以及式(5)可得
式中:I为2×2的单位方阵。
因此系统特征方程为
式中:det(·)为矩阵的行列式。
注意到Zline与ZHVDC均具有主对角元素相等、非对角元素互为相反数的特殊形式,两者的矩阵和以及矩阵和的逆矩阵也具有该特殊形式,因此可以将柔直送端换流站动态与交流线路阻抗合并为![]() 。式(7)可以等价改写为
。式(7)可以等价改写为
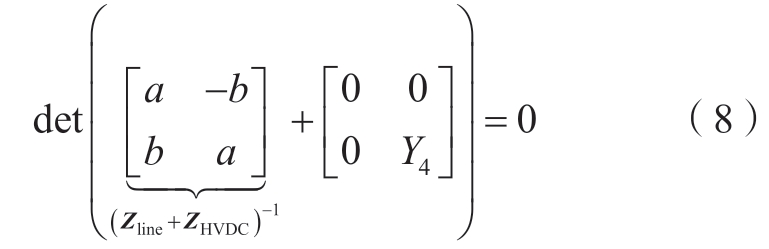
式中:![]() 表示阻抗矩阵具有这种对称形式。
表示阻抗矩阵具有这种对称形式。
通过Schur补将送出系统式(8)所示的MIMO模型降阶为SISO模型,可以得到等价的闭环系统特征方程为
式中:Gol为系统开环传递函数,可以利用Gol的奈奎斯特判据评估送出系统的稳定性。
新能源VSC与电网侧导纳矩阵形式满足文献[23]中广义阻抗/广义导纳定义的条件,因此将新能源柔直送出系统中新能源VSC的广义导纳定义为

根据文献[23]可知,式(10)中Ye2VSC和Ye3VSC均为0。
电网侧阻抗的广义导纳定义为
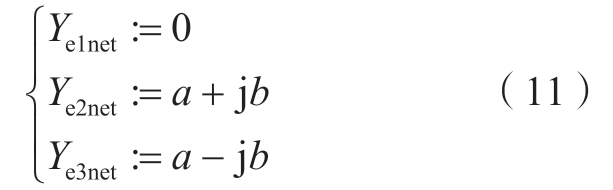
式(11)中Ye2net和Ye3net为极坐标形式下交流电网的正负序导纳。
通过比较式(9)与式(10)—(11),可以得到广义阻抗稳定性判据。
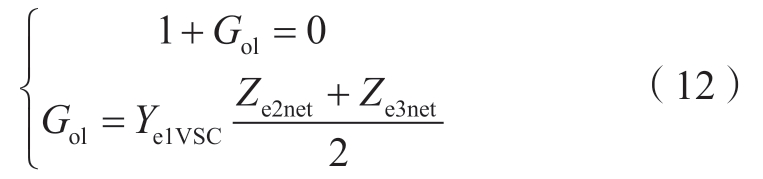
式中:![]() 与Znet1数学表达式等价。
与Znet1数学表达式等价。
为了方便分析振荡机理,式(12)也可以写成
从式 (13) 可知,新能源柔直送出系统的次同步振荡问题可以解释为广义阻抗组成的等效电路的串联谐振问题,如图3所示。当谐振频率处系统的广义阻抗的等效电阻小于0时,系统小干扰失稳。并且广义阻抗分析法的优势在于可以将新能源VSC的动态与电网侧的动态解耦,其中Ze1VSC仅包含新能源VSC的动态,Znet1包含柔直定交流电压外环与交流线路的电网侧动态阻抗,更加清晰地揭示了振荡机理。
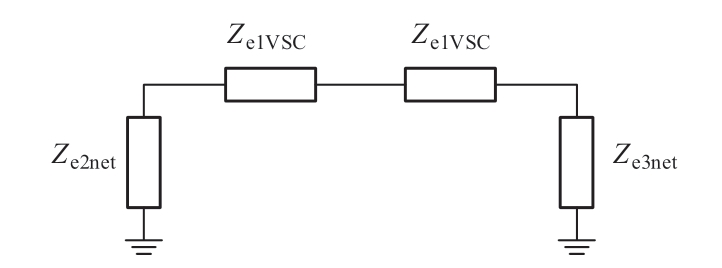
图3 送出系统的广义阻抗等效电路
Fig.3 Generalized impedance equivalent circuit of the output system
2.2 广义阻抗判据适用性讨论
为保证开环传递函数奈奎斯特图判断稳定性的结果有效,满足标称性条件,开环传递函数Gol = Znet1Y4不能存在右半平面(right half plane,RHP)极点。如果Gol存在RHP极点,则存在奈奎斯特曲线包围(-1,j0)点但系统依然稳定的可能性,从而导致判据失效。
在新能源VSC的设计过程中要保证其并入电网是稳定的,所以可以认为变流器的端口特性方程是具有稳定性的,即Y4不存在RHP极点。所以需要关注Znet1是否存在RHP极点。由于![]() 以及
以及![]() 在本文关注的锁相环频段内均近似为1[25],那么系统开环传递函数Gol可以化简为
在本文关注的锁相环频段内均近似为1[25],那么系统开环传递函数Gol可以化简为
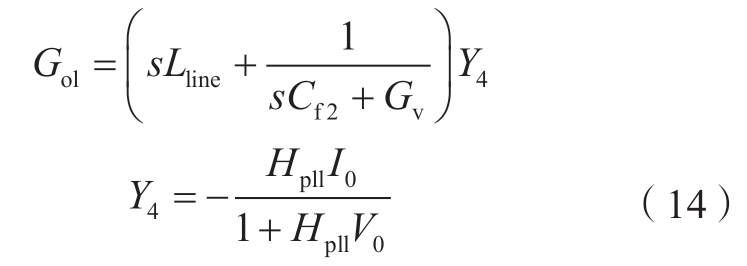
因为Y4不存在RHP极点,那么Gol不存在RHP极点等价于式(15)不存在RHP零点。如果
式中:Kpv、Kiv分别为定交流电压外环PI控制的比例与积分系数。
显然式 (15) 各项系数均是正数,可以利用劳思-赫尔维茨准则判断该一元二次方程不存在RHP零点。所以开环传递函数Gol不存在RHP极点,而正负序阻抗判据会存在RHP极点,存在“裕度反向”问题,无法任意整定互补灵敏度峰值[18]。因此新能源柔直送出场景下广义阻抗判据满足标称性,具有良好的适用性。
该系统的小干扰稳定性可以通过开环传递函数Gol的奈奎斯特曲线是否包围(-1, j0)点来判断,而不必关注包围(-1, j0)点的圈数。如果Gol的奈奎斯特曲线包围(-1, j0)点,系统振荡失稳;如果Gol的奈奎斯特曲线不包围(-1, j0)点,系统是小干扰稳定的。
进一步地,可以通过Gol的奈奎斯特曲线距离(-1, j0)点的最短距离评估送出系统的稳定裕度S,计算表达式如下
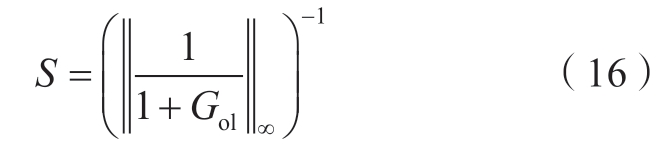
式中:||·||∞表示H∞范数。
另外,新能源柔直送出系统的小干扰稳定性也可以根据如下的等价判据来判断:如果Znet1与Ze1VSC在幅值曲线的每个交点处的相位差均小于180°,那么新能源柔直送出系统是小干扰稳定的。反之,系统是小干扰失稳的。
该等价判据可以通过伯德图进行判断,能够更加清晰反映不同参数对小扰动稳定性的影响。
3 新能源柔直送出系统稳定性影响因素分析
由式(14)可知,送出系统在本文关注频段主要存在新能源VSC锁相环与柔直送端环流站外环控制之间的动态交互,因此本章主要结合广义阻抗分析VSC与柔直送端换流站控制对于小干扰稳定性的影响。
3.1 锁相环参数对稳定性影响
单位功率因数的新能源变流器运行于额定工况下时,式(14)中Y4即为锁相环的闭环传递函数,代入PI控制器传递函数后Y4的表达式如(17)所示,是典型的二阶系统。由于Ze1VSC与Y4的幅相特性曲线具有对称性,那么可以利用Y4的性能指标进行分析。
式中:自然频率![]() ;阻尼比
;阻尼比![]() ;Kipll为VSC锁相环PI控制积分系数;Kppll为VSC锁相环PI控制比例系数。
;Kipll为VSC锁相环PI控制积分系数;Kppll为VSC锁相环PI控制比例系数。
本文新能源柔直送出标称系统仿真模型与理论解析模型采用的参数如表1所示。
表1 仿真参数
Table 1 Parameters of simulation

参数 数值系统容量基准值Sb/kVA 1500系统电压基准值Ub/kV 35新能源电流内环比例系数Kpi 0.6新能源电流内环积分系数Kii 15新能源锁相环比例系数Kppll 20新能源锁相环积分系数Kipll 300新能源电压前馈系数Tff/s 0.001柔直电流内环比例系数Kpih 0.4柔直电流内环积分系数Kiih 10柔直电压外环比例系数Kpv 5柔直电压外环积分系数Kiv 30滤波电感Lf1、Lf2/pu 0.05滤波电感Cf1、Cf2/pu 0.05线路电感Lline/pu 0.1
图4给出了不同锁相环比例系数时的伯德图,其他参数均保持不变。
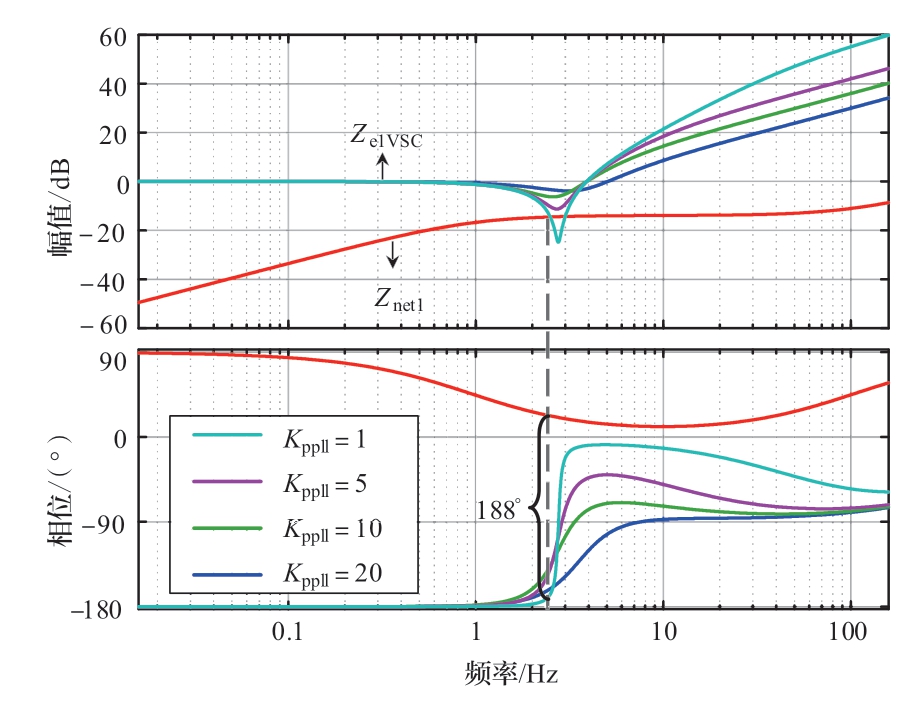
图4 不同VSC锁相环比例系数下的伯德图
Fig.4 Bode plot with different proportional factor of PLL
从图4中可以看出,随着锁相环比例系数Kppll的减小,二阶系统阻尼比ξ不断减小。当阻尼比ξ小于0.707时,Ze1VSC的幅值曲线在锁相环谐振频率处出现谐振峰,并且随着阻尼比的增大,Ze1VSC的幅值曲线逐渐与Znet1的幅值曲线相交,若此时Znet1与Ze1VSC交点处的相位差大于180°,导致系统失稳。反之,当锁相环比例系数增大时,锁相环阻尼比增大,不会出现谐振峰值,此时Ze1VSC幅值曲线不容易与Znet1的幅值曲线相交,系统稳定。
另一方面,保持其他参数不变,增大锁相环积分系数,二阶系统的阻尼比ξ逐渐减小,同时系统谐振频率增大,这样会增大系统失稳风险。不同锁相环积分系数对应的伯德图如图5所示。
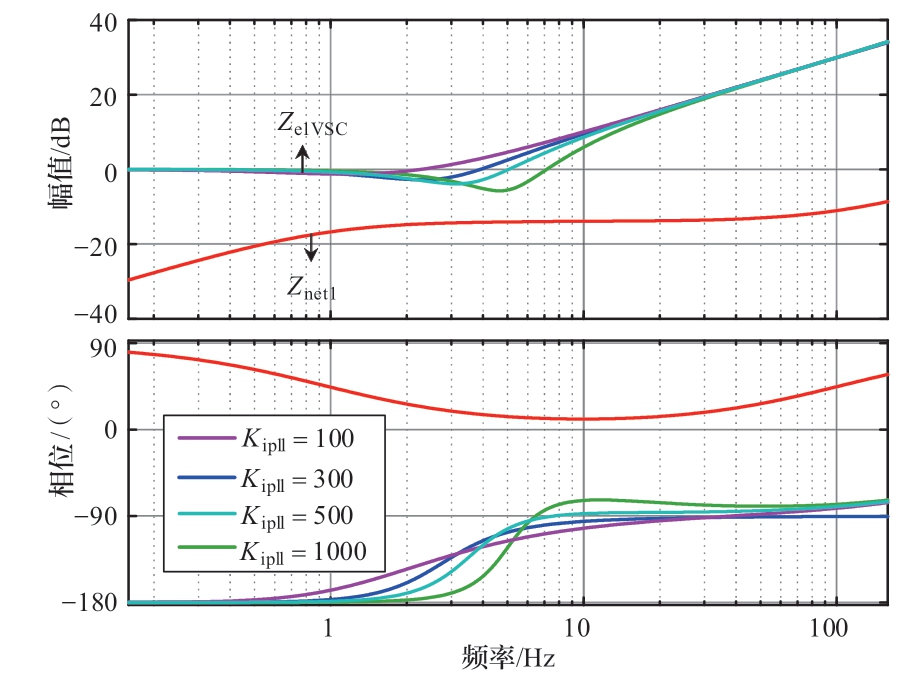
图5 不同VSC锁相环积分系数下的伯德图
Fig.5 Bode plot with different integral factor of PLL
3.2 柔直送端换流站外环参数对稳定性的影响
不同柔直送端换流站外环PI控制环节的比例系数对应的伯德图如图6所示,随着比例系数Kpv的减小,Znet1的幅值逐渐接近0 dB。如果此时锁相环比例系数过小或者积分系数过大,导致Ze1VSC对应的幅值曲线出现谐振峰,会增大系统失稳风险。
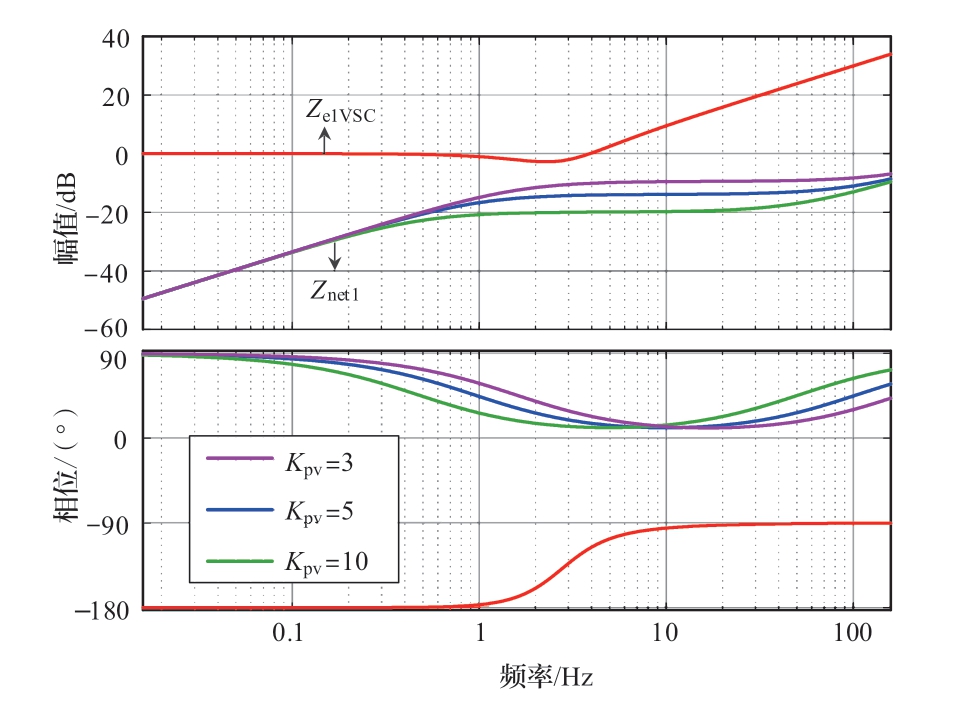
图6 不同柔直换流站外环比例系数下的伯德图
Fig.6 Bode plot with different proportional factor of outer loop of VSC-HVDC
图7展示了柔直送端换流站外环的不同积分系数对应的Znet1与Ze1VSC的伯德图。改变换流站外环的积分系数主要影响了Znet1的幅值曲线低频部分的拐点,如果积分系数减小,幅值曲线的拐点会更靠近低频,并且相位拐点会滞后。
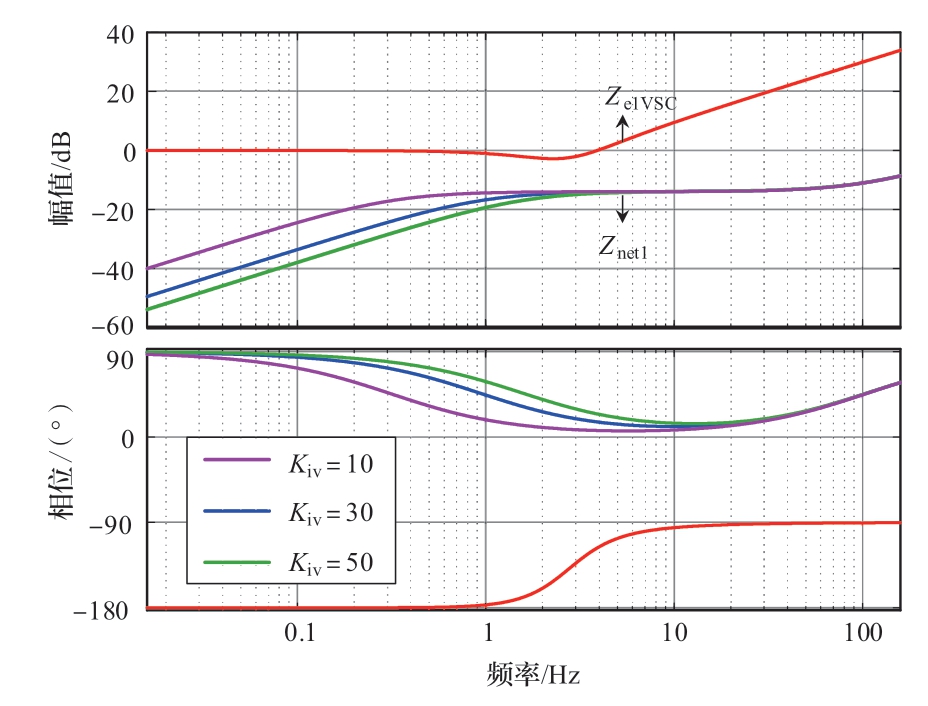
图7 不同柔直换流站外环积分系数下的伯德图
Fig.7 Bode plot with different integral factor of outer loop of VSC-HVDC
4 新能源柔直送出系统稳定性提升方法
第3章提出了新能源柔直送出系统的广义阻抗判据,并分析了小干扰稳定性影响因素。本章从广义阻抗出发提出稳定性提升方法,实现振荡抑制。
式(13)中Ze1VSC表达式可以写为
式中: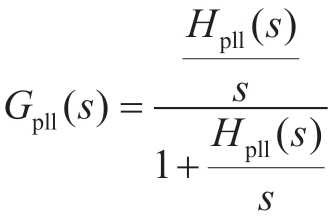 ;Hpll为锁相环的传递函数。
;Hpll为锁相环的传递函数。
系统失稳主要是由于Ze1VSC的幅值曲线出现谐振峰从而与Znet1的幅值曲线相交。如图4所示,交点处Ze1VSC的相频曲线接近-180°,而Znet1的相位处于0到90°之间,两者相位差容易超过180°导致系统失稳。因此稳定性提升的思路为抑制Ze1VSC幅值曲线出现谐振峰,防止Ze1VSC与Znet1幅值曲线相交,同时计算出稳定裕度S,选出稳定裕度S最大对应的参数。设谐振峰值对应的谐振频率设为ωc,此时Gpll相位接近0°,即Gpll在谐振频率ωc处约为1+j0,那么在谐振频率ωc处Ze1VSC的幅值接近于0,所以Ze1VSC在谐振频率ωc处出现峰值。
为避免Gpll(jωc ) 接近1+j0,可在锁相环处串联超前滞后校正环节,如图8所示,![]() 的相位减小至-60°左右,相位校正后Ze1VSC在谐振频率ωc处幅值接近1,避免了与Znet1的幅值曲线相交,从而达到稳定性提升目的,校正前后的示意图参见图9。超前滞后环节的传递函数Gc的形式如下:
的相位减小至-60°左右,相位校正后Ze1VSC在谐振频率ωc处幅值接近1,避免了与Znet1的幅值曲线相交,从而达到稳定性提升目的,校正前后的示意图参见图9。超前滞后环节的传递函数Gc的形式如下:
图8 锁相环相位校正
Fig.8 Phase Correction of PLL
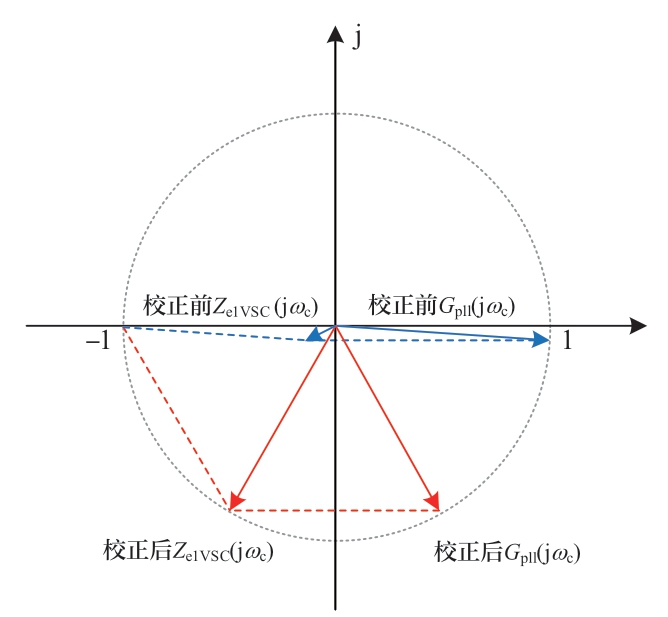
图9 锁相环校正前后Ze1VSC对比
Fig.9 Comparison of Ze1VSC before and after PLL correction
式中:α为超前滞后系数;T为时间常数。
若Gc提供相位超前效应,那么![]() 提供相位滞后效应,最大相位滞后为
提供相位滞后效应,最大相位滞后为
最大的相位滞后φ出现的最大滞后频率点flag为
根据上述分析,需要对锁相环在谐振频率处的幅相特性曲线进行校正整形,那么flag选取为谐振峰出现的频率ωc,最大相位滞后φ设置为60°左右,带入式(20)—(21)即可求解α与T的数值。
确定提升方法采用的校正环节后,还需要确定合适的参数,计算出参数区间内不同参数对应的稳定裕度S,选出稳定裕度S最大对应的参数。具体提升方法流程图如图10所示。
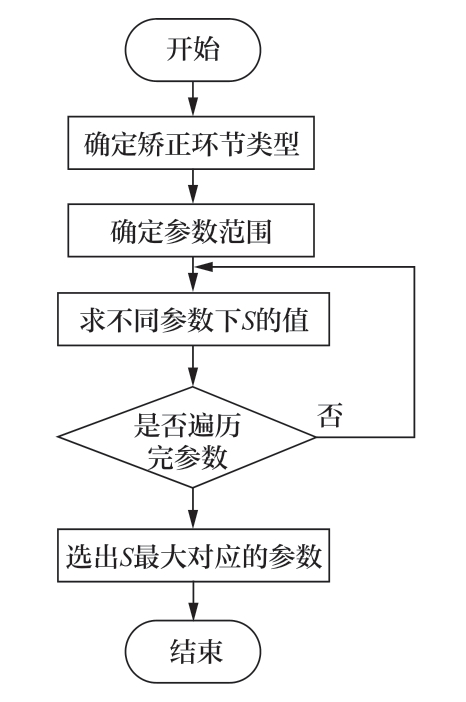
图10 所提稳定性提升方法的流程图
Fig.10 Flowchart of proposed stability improvement method
5 仿真验证
5.1 广义阻抗稳定性判据有效性验证
为验证第2章提出的广义阻抗判据的等价性与准确性,本章将式(9)解得的理论解析模型闭环系统主导特征根与Matlab/Simulink仿真模型在稳定工作点线性化求得的状态空间矩阵的主导特征根进行对比,其中原系统的特征值通过Matlab/Simulink中搭建模型的状态空间方程计算得到,特征子系统的特征值通过Matlab编程计算得到。仿真模型与理论解析模型均采用表1的参数。结果如图11所示,解析模型与仿真模型的主导特征根一致,证明了本文提出的系统特征方程解析模型的正确性。
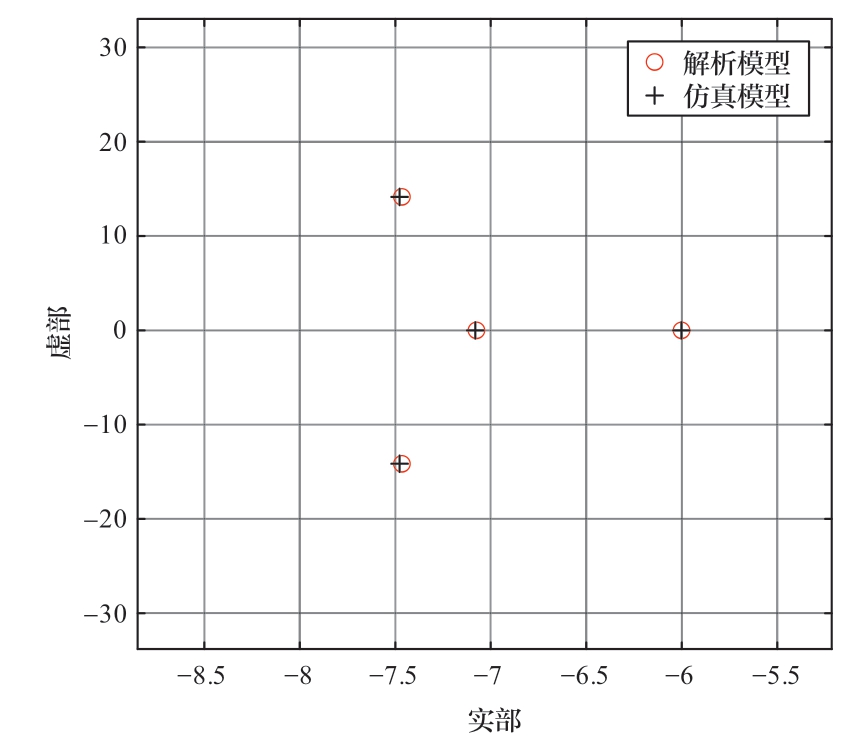
图11 2种模型的主导特征根对比
Fig.11 Comparison of dominant characteristic roots of two models
为进一步验证所提判据的准确性,本文采用2组控制参数进行时域仿真验证,案例1参数见表1。具体仿真验证思路如下:系统达到稳定工作点后,在柔直送端换流站并网点注入电压阶跃小扰动并在短时间内切除,通过观察新能源并网点x轴电压Vx波形判断系统是否小干扰失稳,并与式(14)表示的开环奈奎斯特图进行对比。
解析模型的稳定裕度为0.081 1,仿真模型的稳定裕度为0.080 3,2种模型的稳定裕度基本相同。
图12展示了案例1中新能源VSC并网点电压x轴分量的时域仿真波形,可以看到t = 5 s时在柔直并网点注入电压扰动信号并切除,扰动切除后波形迅速收敛,系统稳定。图13的开环传递函数奈奎斯特曲线不包围(-1, j0)点,判稳结果为系统是小干扰稳定的,与时域仿真结果一致。
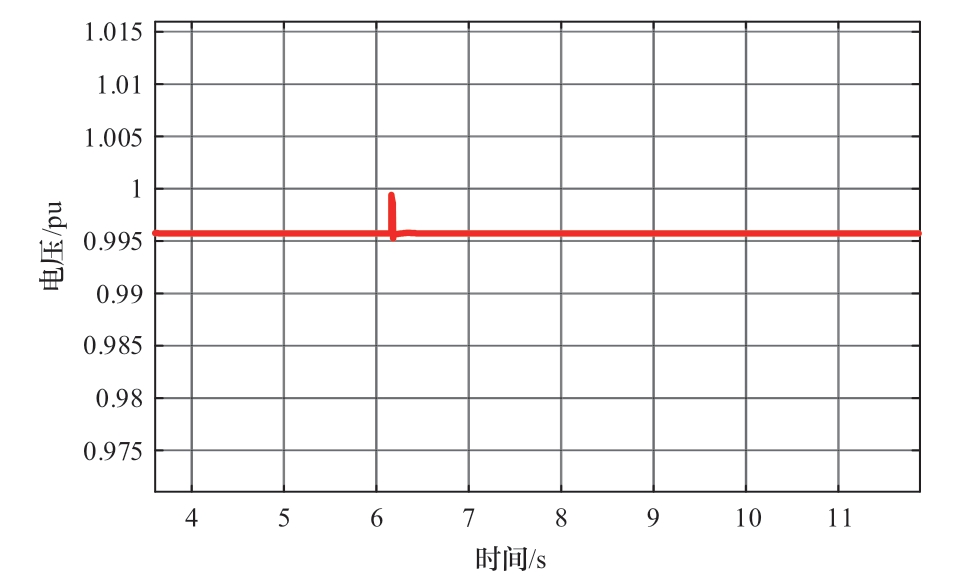
图12 案例1时域波形图
Fig.12 Waveform diagram of Case 1
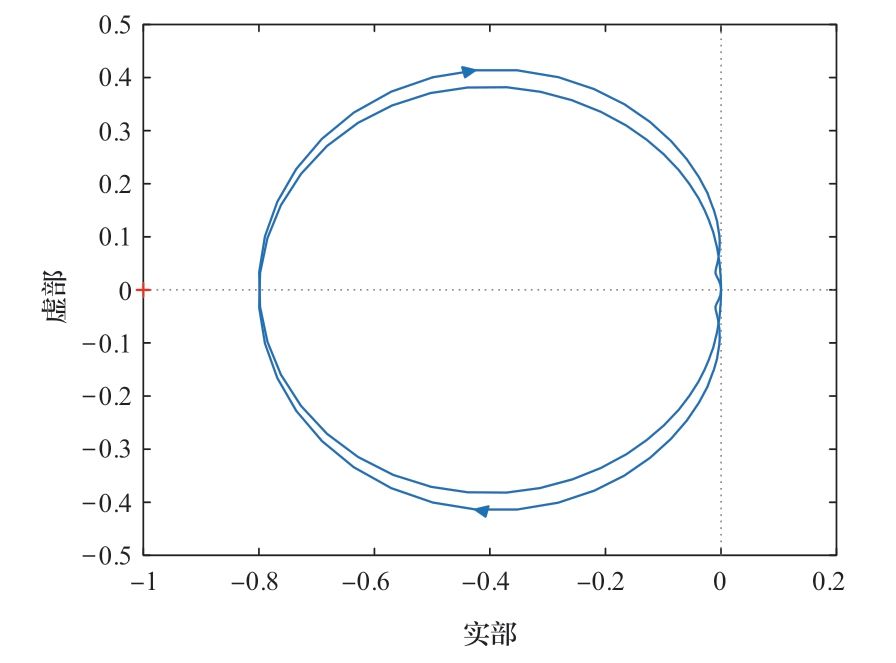
图13 案例1奈奎斯特图
Fig.13 Nyquist plot of Case1
案例2的仿真参数仅改变了新能源VSC锁相环的PI控制参数:比例系数Kppll = 2,积分系数Kipll = 3000,其他主电路及控制系统参数均与案例1相同。图14展示了案例2中新能源并网点电压x轴分量的时域波形,可以看到加入扰动后新能源机端电压振荡发散,系统小干扰失稳。图15的开环传递函数Gol奈奎斯特曲线包围(-1, j0)点,判断系统失稳。案例2中电压的振荡频率为13.6 Hz,对应角频率为85.43,主导极点为0.85+j85.431 5,阻尼比为0.009 6,通过图14波形理论计算的振荡频率为13.9 Hz,验证了理论分析特征根的准确性。案例1与案例2的判断结果均与时域仿真结果一致,验证了本文所提的基于广义阻抗判据的稳定性评估的有效性。
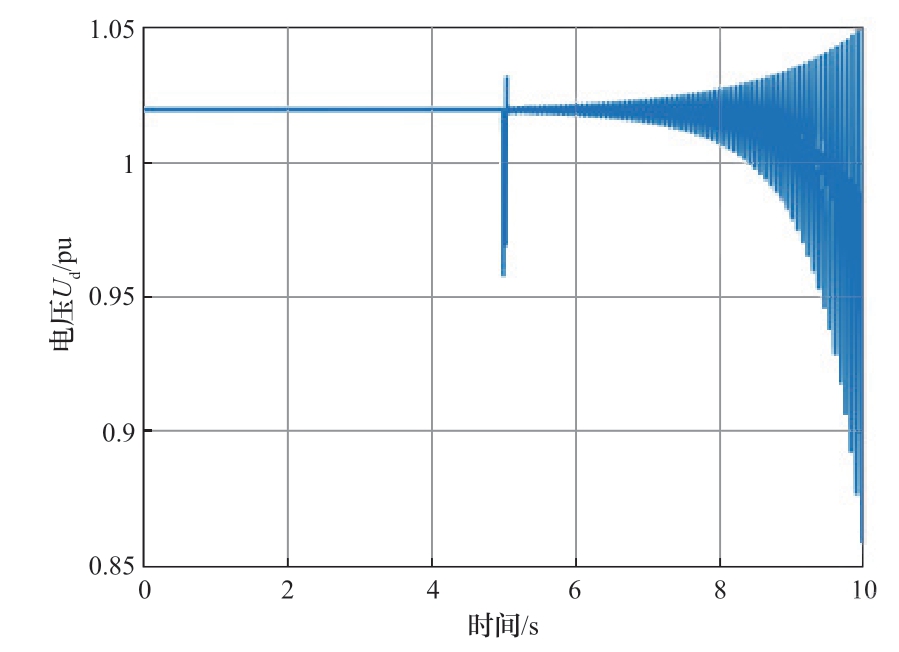
图14 案例2时域波形图
Fig.14 Waveform diagram of Case 2
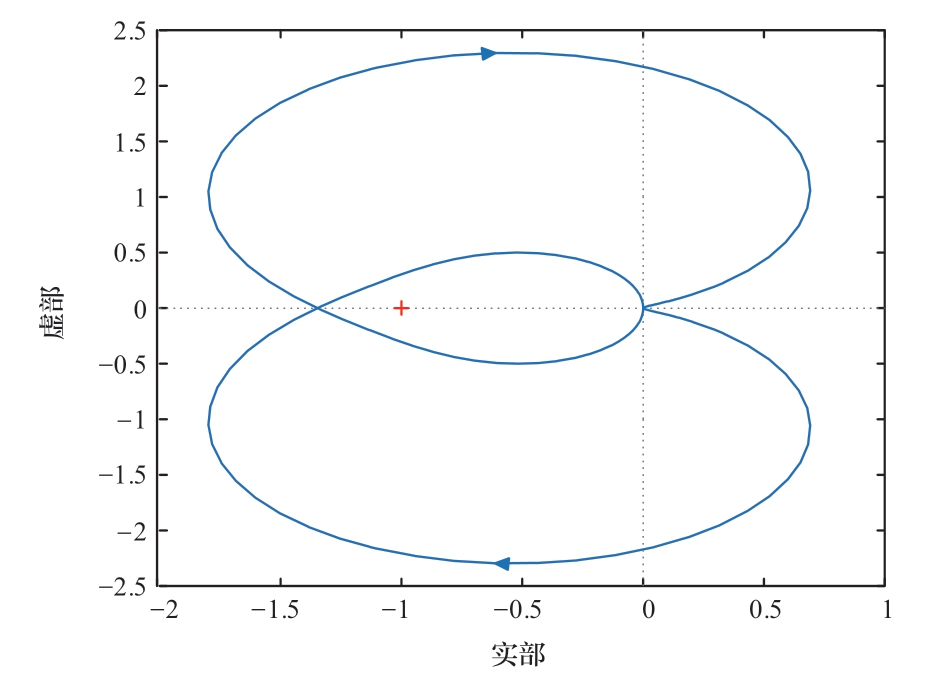
图15 案例2奈奎斯特图
Fig.15 Nyquist plot of Case 2
5.2 稳定性提升方法有效性验证
本节针对小干扰失稳案例的新能源VSC锁相环进行相位校正,其中锁相环PI控制比例系数Kppll = 1,Kipll =1000;柔直外环PI控制比例系数Kpv = 1,Kiv = 30,其他参数与表1相同。图15中校正前Ze1VSC的谐振峰比较明显,且Ze1VSC与Znet1幅值曲线交点处的相位差超过180°,系统失稳。Ze1VSC幅值曲线谐振峰出现的频率在2.757 8 Hz,那么代入 (21) 超前滞后校正的滞后频率,并且最大相位滞后设为60°,计算可得αT =0.215 38 s,T =0.015 46 s。校正后Ze1VSC的幅值曲线谐振峰明显减小,避免与Znet1幅值曲线相交,如图16所示。
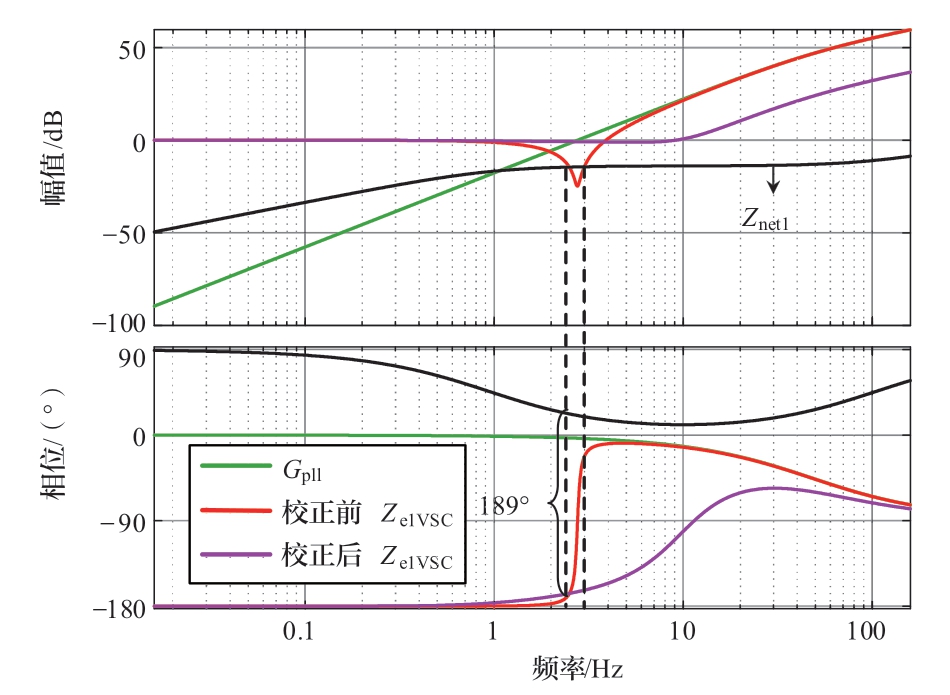
图16 校正前后的伯德图
Fig.16 Bode plot before and after PLL correction
校正前的稳定裕度S为0.067 3,校正后为0.079 2,可以看出添加超前滞后校正环节后,稳定裕度有所提升,即在小干扰情况下更加稳定。
在Simulink中进行了相应的时域仿真来验证所提振荡抑制方法的可行性。在t = 5 s时向柔直送端换流站并网点电压注入小扰动,并于t = 30 s时投入超前滞后环节进行相位校正,从图17所示的新能源变流器机端电压x轴y轴分量波形可以看到,t = 5 s注入小扰动后系统振荡失稳,加入校正环节后振荡被迅速抑制,系统恢复稳定。因此本文所提的锁相环相位校正方法可以提升送出系统的小干扰稳定性,实现次同步频段的振荡的抑制。
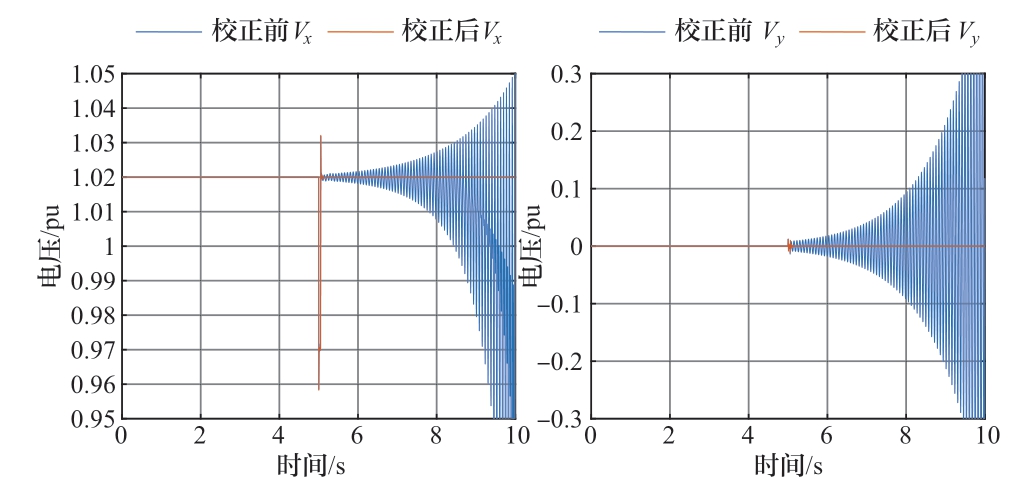
图17 振荡抑制方法的时域仿真验证
Fig.17 Time-domain simulation verification of oscillation suppression methods
6 结论
本文针对新能源柔直送出系统在锁相环主导频段的小干扰稳定性问题,提出了基于广义阻抗判据的系统稳定性评估与提升方法,并且探讨了广义阻抗判据在新能源柔直送出系统的适用性,将广义阻抗分析方法进一步拓展到新能源柔直送出场景中,未来将进一步研究柔直送出系统的暂态稳定性评估方法。本文研究结论如下:
1)考虑新能源柔直送出场景,广义阻抗判据中开环传递函数不存在右半平面极点,满足标称性要求,因此可以通过开环传递函数奈奎斯特曲线在复平面是否包围(-1, j0)判断系统的稳定性,适用于分析评估锁相环主导的次同步振荡风险。
2)新能源柔直送出系统次同步振荡由新能源变流器锁相环与柔直送端换流站定交流电压外环交互导致,其中新能源变流器锁相环阻尼比大于0.707更有利于提升系统的小干扰稳定性。
3)提出了基于锁相环相位校正的系统小干扰稳定性提升方法,可以有效抑制新能源柔直送出系统的次同步振荡,具有工程指导意义。
参考文献
-
[1]
王雪林,钟海旺.新型电力系统背景下抽水蓄能和新型储能协同发展研究[J].全球能源互联网,2024,7(4):363-371.WANG Xuelin, ZHONG Haiwang.Research on synergistic development of pumped storage and new energy storage under the background of new power system[J].Journal of Global Energy Interconnection, 2024, 7(4): 363-371(in Chinese). [百度学术]
-
[2]
文卫兵,赵峥,李明,等.海上风电柔性直流系统设计及工程应用[J].全球能源互联网,2023,6(1):1-9.WEN Weibing, ZHAO Zheng, LI Ming, et al.Design and engineering application of offshore wind power VSC-HVDC system[J].Journal of Global Energy Interconnection, 2023,6(1): 1-9(in Chinese). [百度学术]
-
[3]
赖逸洋,王增平,王彤.电流差动保护在柔直接入的交流电网中适应性分析及改进措施研究[J].电力系统保护与控制,2023,51(3):145-154.LAI Yiyang,WANG Zengping,WANG Tong.Adaptability analysis of current differential protection in an AC power grid withan MMC-HVDC and improvement measures[J].Power System Protection and Control, 2023, 51(3): 145-154 (in Chinese). [百度学术]
-
[4]
高正创,李凤婷,解超,等.基于电压行波陡度的柔性直流送出线路快速保护方案[J].电力工程技术,2023,42(4):84-93.GAO Zhengchuang, LI Fengting, XIE Chao, et al.Fast protection scheme for flexible DC transmission line based on voltage traveling wave steepness[J].Electric Power Engineering Technology, 2023, 42(4): 84-93 (in Chinese). [百度学术]
-
[5]
吕敬,董鹏,施刚,等.大型双馈风电场经MMC-HVDC并网的次同步振荡及其抑制[J].中国电机工程学报,2015,35(19):4852-4860.LÜ Jing, DONG Peng, SHI Gang, et al.Subsynchronous oscillation and its mitigation of MMC-based HVDC with large doubly-fed induction generator-based wind farm integration[J].Proceedings of the CSEE, 2015, 35(19): 4852-4860(in Chinese). [百度学术]
-
[6]
魏伟,许树楷,李岩,等.南澳多端柔性直流输电示范工程系统调试[J].南方电网技术,2015,9(1):73-77.WEI Wei, XU Shukai, LI Yan, et al.The system commissioning of Nan’ao VSC-MTDC demonstration project[J].Southern Power System Technology, 2015, 9(1):73-77(in Chinese). [百度学术]
-
[7]
郑少明,刘一民,董鹏,等.张北工程风电柔直汇集系统次、超同步振荡分析[J].全球能源互联网,2023,6(6):608-617.ZHENG Shaoming, LIU Yimin, DONG Peng, et al.Analysis of sub-synchronous and super-synchronous oscillation of wind power flexible direct gathering system in Zhangbei Project[J].Journal of Global Energy Interconnection, 2023, 6(6): 608-617(in Chinese). [百度学术]
-
[8]
尹聪琦,谢小荣,刘辉,等.柔性直流输电系统振荡现象分析与控制方法综述[J].电网技术,2018,42(4):1117-1123.YIN Congqi, XIE Xiaorong, LIU Hui, et al.Analysis of oscillation phenomenon and summary of control methods in flexible DC transmission system[J].Power System Technology, 2018, 42(4): 1117-1123(in Chinese). [百度学术]
-
[9]
BUCHHAGEN C, RAUSCHER C, MENZE A, et al.First experiences with harmonic interactions in converter dominated grids[C]//International ETG Congress 2015, Bonn, Germany,2015: 1-7. [百度学术]
-
[10]
吴俊,方芳,赵晓明.柔性直流输电舟洋换流站无源HVDC启动试验中典型故障分析[J].浙江电力,2016,35(1):6-9.WU Jun, FANG Fang, ZHAO Xiaoming.Analysis on typical faults in passive HVDC startup tests in Zhouyang VSC-HVDC converter station[J].Zhejiang Electric Power, 2016, 35(1):6-9(in Chinese). [百度学术]
-
[11]
邵冰冰,赵书强,高本锋,等.多直驱风机经VSC-HVDC并网系统场内/场网次同步振荡特性分析[J].中国电机工程学报,2020,40(12):3835-3847.SHAO Bingbing, ZHAO Shuqiang, GAO Benfeng, et al.Analysis of sub-synchronous oscillation characteristics of multi-direct-drive fans in VSC-HVDC grid-connected system[J].Proceedings of the CSEE, 2020, 40(12): 3835-3847(in Chinese). [百度学术]
-
[12]
郭贤珊,李云丰,谢欣涛,等.直驱风电场经柔直并网诱发的次同步振荡特性[J].中国电机工程学报,2020,40(4):1149-1160, 1407.GUO Xianshan, LI Yunfeng, XIE Xintao, et al.Subsynchronous oscillation characteristics caused by PMSGbased wind plant farm integrated via flexible HVDC system[J].Proceedings of the CSEE.2020, 40(4): 1149-1160, 1407 (in Chinese). [百度学术]
-
[13]
王洪耀,张英敏,廖建权,等.基于阻抗灵敏度分析的柔直并网系统中高频谐振抑制策略[J].电网技术,2023,47(10):4311-4323.WANG Hongyao, ZHANG Yingmin, LIAO Jianquan, et al.Medium- and high-frequency resonance suppression strategy in flexible direct grid connected system based on impedance sensitivity analysis[J].Power System Technology, 2023,47(10): 4311-4323(in Chinese). [百度学术]
-
[14]
LIU H C, SUN J.Voltage stability and control of offshore wind farms with AC collection and HVDC transmission[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2014, 2(4): 1181-1189. [百度学术]
-
[15]
孙焜,姚伟,周毅,等.基于SISO序阻抗的直驱风场经柔直输电系统中频振荡机理分析及抑制[J].中国电机工程学报,2023,43(2):442-454.SUN Kun, YAO Wei, ZHOU Yi, et al.Mechanism analysis and suppression of medium-frequency oscillation based on the SISO impedance in a PMSG-based wind farm when connected to a VSC-HVDC[J].Proceedings of the CSEE, 2023, 43(2):442-454(in Chinese). [百度学术]
-
[16]
吕敬,蔡旭,张占奎,等.海上风电场经MMC-HVDC并网的阻抗建模及稳定性分析[J].中国电机工程学报,2016,36(14):3771-3781.LÜ Jing, CAI Xu, ZHANG Zhankui, et al.Impedance modeling and stability analysis of offshore wind farms connected to the grid via MMC-HVDC[J].Proceedings of the CSEE, 2016, 36(14): 3771-3781(in Chinese). [百度学术]
-
[17]
艾力西尔·亚尔买买提,辛焕海,宫泽旭,等.锁相环主导下变流器振荡问题的阻抗分析方法:标称性与鲁棒性[J].中国电机工程学报,2024,44(15):6035-6047.YAERMAIMAITI Ailixier, XIN Huanhai, GONG Zexu, et al.Impedance analysis method of oscillation issues in converter caused by phase-locked loop: nominal performance and robustness[J].Proceedings of the CSEE, 2024, 44(15): 6035-6047(in Chinese). [百度学术]
-
[18]
宫泽旭,艾力西尔·亚尔买买提,辛焕海,等.新能源电力系统并网设备小扰动稳定分析(一):机理模型与稳定判据适用性[J].中国电机工程学报,2022,42(12):4405-4419.GONG Zexu, YAERMAIMAITI Ailixier, XIN Huanhai, et al.Small signal stability analysis of equipment in renewable energy power system(part Ⅰ): mechanism model and adaptation of stability criterion[J].Proceedings of the CSEE,2022, 42(12): 4405-4419(in Chinese). [百度学术]
-
[19]
马富艺龙,辛焕海,刘晨曦,等.新能源基地柔性直流送出系统小扰动电压支撑强度评估[J].电工技术学报,2023,38(21):5758-5770.MA Fuyilong, XIN Huanhai, LIU Chenxi, et al.Smalldisturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system[J].Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770(in Chinese). [百度学术]
-
[20]
ZHAO M Q, YUAN X M, HU J B, et al.Voltage dynamics of current control time-scale in a VSC-connected weak grid[J].IEEE Transactions on Power Systems, 2015, 31(4): 2925-2937. [百度学术]
-
[21]
张志强,李秋彤,余浩,等.海上直驱风电经柔直并网系统的次/超同步振荡特性分析[J].上海交通大学学报,2022,56(12):1572-1583.ZHANG Zhiqiang, LI Qiutong, YU Hao, et al.Analysis of subsynchronous and super-synchronous oscillation characteristics of offshore direct-driven wind power via flexible direct gridconnected system[J].Journal of Shanghai Jiao Tong University,2022, 56(12): 1572-1583(in Chinese). [百度学术]
-
[22]
王锡凡.现代电力系统分析[M].北京:科学出版社,2003.WANG Xifan.Analysis of modern power system[M].Beijing:Science Press, 2003(in Chinese). [百度学术]
-
[23]
辛焕海,李子恒,董炜,等.三相变流器并网系统的广义阻抗及稳定判据[J].中国电机工程学报,2017,37(5):1277-1293.XIN Huanhai, LI Ziheng, DONG Wei, et al.Generalizedimpedance and stability criterion for grid-connected converters[J].Proceedings of the CSEE, 2017, 37(5): 1277-1293(in Chinese). [百度学术]
-
[24]
HUANG L B, XIN H H, LI Z Y, et al.Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control[J].IEEE Transactions on Smart Grid, 2019, 11(1): 501-516. [百度学术]
-
[25]
杨超然,宫泽旭,洪敏,等.外环动态影响下变流器广义阻抗判据的适用性分析[J].中国电机工程学报,2021,41(9):3012-3024.YANG Chaoran, GONG Zexu, HONG Min, et al.Applicability analysis of the generalized-impedance stability criterion for converters considering the outer-loop dynamics[J].Proceedings of the CSEE, 2021, 41(9): 3012-3024(in Chinese). [百度学术]
基金项目
南方电网公司科技项目(036000KK52220018(GDKJXM20220249))。
Science and Technology Foundation of China Southern Power Grid Company Limited (036000KK52220018(GDKJXM20220249)).


