相关论文:
-

-
全球能源互联网
第8卷 第5期 2025年09月;页码:636-650
考虑多重不确定性的综合能源系统与加氢站主从博弈鲁棒定价策略
Robust Pricing Strategy Based on Stackelberg Game for Integrated Energy System and Hydrogen Refueling Station Considering Multiple Uncertainties
- 1.华北电力大学经济与管理学院,北京市 昌平区 102206
- 2.新能源电力与低碳发展研究北京市重点实验室,北京市 昌平区 102206
- LI Jinchao1,2, LAN Xinyi1*, WU Zijing1, HE Jiaming1 (1. School of Economics and Management, North China Electric Power University, Changping District, Beijing 102206, China
- 2. Beijing Key Laboratory of New Energy and Low-Carbon Development, Changping District, Beijing 102206, China
关键词
Keywords
摘 要
Abstract
综合能源系统与加氢站联合运营受到交易价格不完善以及运行环境不确定的制约,为此构建了基于Stackelberg博弈的综合能源系统与加氢站联合运营鲁棒定价模型。首先,该模型以综合能源系统运营商为领导者,采用两阶段鲁棒优化方法处理可再生能源和负荷的不确定性,以自身成本最小化为目标制定交易电价;加氢站作为跟随者根据自身需求对电价做出响应,实现购能成本最小化,并用分布式鲁棒机会约束处理氢负荷需求的不确定性。然后,为解决模型中多重不确定性造成的求解难题,在较为宽松的条件下证明了该模型下Slater条件的成立,采用Karush-Kuhn-Tucker条件和大M法对定价模型进行重新表述,并利用商业求解器 YALMIP/GUROBI进行了求解。最后,通过算例仿真验证了所提模型和方法的有效性。
The joint operation of integrated energy system and hydrogen refueling station is restricted by imperfect transaction price and uncertain operation environment. Therefore, this paper constructs a robust pricing model for the joint operation of integrated energy system and hydrogen refueling station based on Stackelberg game. Firstly, the model takes the integrated energy system operator as the leader, adopts a two-stage robust optimization method to deal with the uncertainty of renewable energy and load, and sets the transaction tariff with the goal of minimizing its own cost; the hydrogen refueling station responds to the tariff according to its own demand as a follower to minimize the cost of purchasing energy, and deals with the uncertainty of the demand of the hydrogen load by using the distributionally robust chance constraint. Then, in order to solve the solution difficulties caused by multiple uncertainties in the model, this paper proves that Slater’s condition holds under a mild assumption, reformulates the pricing model by using the Karush-Kuhn-Tucker condition and the Big M method, and solves the problem by using the commercial solver YALMIP/GUROBI. Finally, the validity of the proposed model and method is verified by arithmetic simulation.
0 引言
近些年随着能源系统改革,涌现了许多新业态,交易主体逐渐增多,例如综合能源系统[1](integrated energy system,IES)、充电站(charging stations,CS)、加氢站[2-3] (hydrogen refueling station,HRS)等。综合能源系统具有多能互补的优点,能够满足用户多元化需求、拓展企业盈利空间、提升社会整体能效。氢能以其清洁低碳、灵活高效的特性被广泛认为是极具前景的传统能源的替代品,可以缓解温室效应和化石燃料危机[4-5],因此,与氢能相关的新业态快速兴起。根据中国《氢能产业发展中长期规划(2021—2035)》,截至2025年全国将推广氢燃料车5万辆,并部署建设一批加氢站[6]。氢能在终端领域的普及和利用能够促进社会深度脱碳,对能源绿色转型发展起到重要支撑作用。综合能源系统与加氢站的联合运营有助于提高双方运行经济性和促进能源系统的低碳转型。
目前对于IES联合运营的研究对象多数为CS[7-9],尽管与CS联合运营可以指导电动汽车 (electric vehicle,EV)合理充放电缓解电网压力,但是EV需满足用户出行需求,因此其功率可调时间和可用能量受限于具有不确定性的用户行为[10]。对于氢能来说,其易于储存,制备和使用不需要同时进行,并且还可以通过电转氢、氢转电技术实现多能耦合转化,这些使得氢能在功率可调时间和可用能量方面更具灵活性[11]。因此,对于IES与HRS的联合运营研究十分有必要。
当前国内外学者就含氢的IES运行优化和含可再生能源发电的制氢系统[11-14]运行调度展开了一系列研究。文献[15]计及电制氢和碳捕集的园区综合能源系统动态规划方法,通过电制氢促进了电能就地消纳并且提升了收益。文献[16]提出一种考虑电热柔性负荷及氢能精细化建模的H2-IES低碳运行方法,充分发挥氢能在综合能源系统中的效用,有效挖掘氢能的能源利用潜力、降低系统碳排放。文献[17]提出了一种含海上风电制氢的IES分布鲁棒低碳优化运行方法,考虑了IES源荷不确定性,对氢能进行了充分及灵活运用,从而降低了碳排放和运营成本。文献[18]提出了一个由风电光伏系统驱动的制氢系统和多个加氢系统(HRSs) 规划模型。文献[19]提出了一种基于可再生能源的离网地区电/氢/气/加气站,其中考虑了风电和光伏电力的不确定性和电动汽车、氢燃料汽车和天然气汽车的需求不确定性。上述研究均将电能和氢能看作同属一个利益主体,忽略了二者利益冲突或者二者不同属一个利益主体情况,缺乏与两者交互相关的价格机制研究。
针对现有文献的不足,本文提出IES运营商和加氢站运营商两个利益主体联合运营下的鲁棒主从定价方法,利用Stackelberg模型理论来描述二者在多种不确定性下的交互行为。这个定价模型是一个双层框架。模型上层,IES面临的光伏发电(photovoltaic,PV)、风力发电(wind turbine,WT)和电热负荷等外部不确定性具有明确的边界但难以精确描述其概率分布,因此IES运营商采用两阶段鲁棒优化(two-stage robust optimization, TSRO)模型对PV、WT和电热负荷不确定性下的电价和调度方案进行优化。模型下层HRS对氢气需求的不确定性仅掌握具有一定的概率分布信息,对需求边界以及分布本身不完全确定。在这种情况下,分布鲁棒机会约束(distributionally robust chance constraint,DRCC)能够平衡鲁棒性和经济性,因此模型下层采用分布鲁棒机会约束优化模型对氢气需求的不确定性条件下的购能方案进行优化。然后,本文将该模型转化为一个可以有效求解的经典TSRO问题。案例研究证明了所提方法的有效性。
1 IES与HRS交易模型
1.1 IES与HRS联合运营框架
本文讨论的IES和HRS联合运营模式如图1所示。IES中含有光伏发电(photovoltaic,PV)、风力发电(wind turbine,WT)、热电联产(combined heat and power,CHP)、燃气锅炉(gas boiler,GB)、储能系统(energy storage system,ESS)以及电热负荷,并与HRS、上级电网连接。
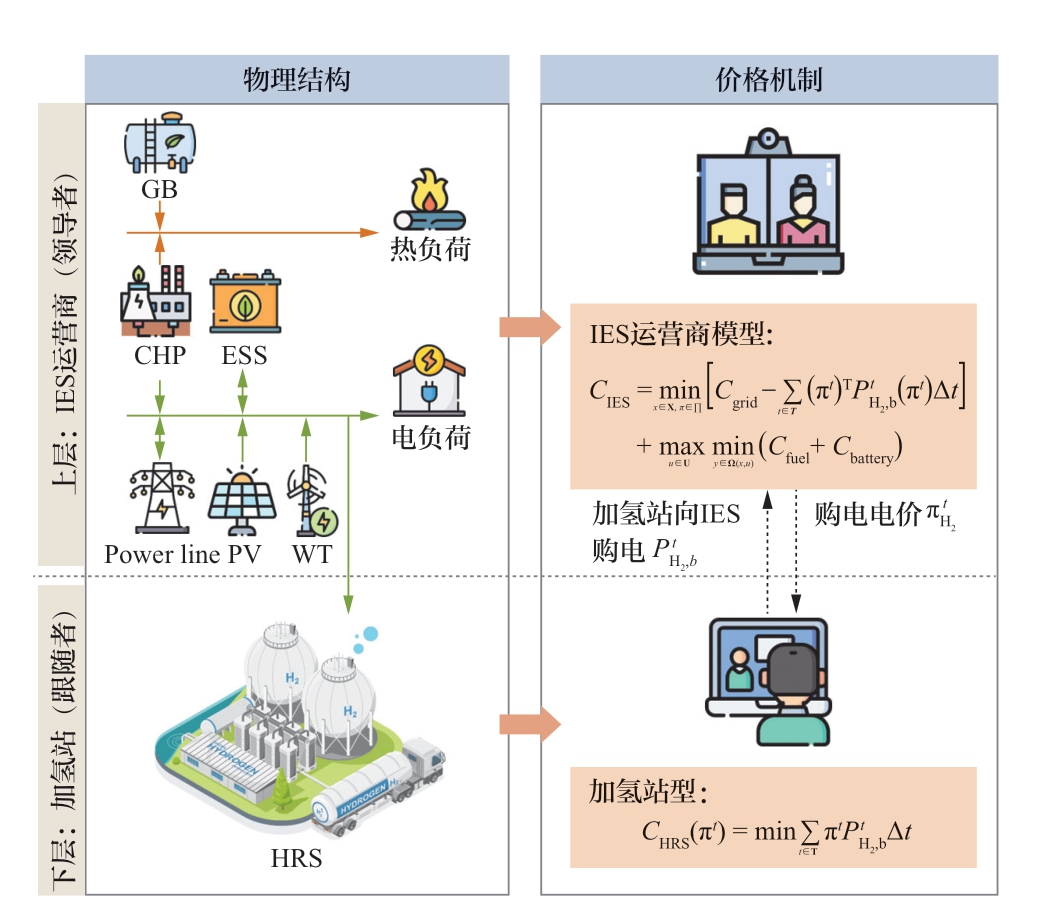
图1 联合运营模式示意图
Fig. 1 Schematic diagram of the joint operation model
HRS则含有电转氢(power to hydrogen,P2H)和氢转电(hydrogen to power,H2P)设备、储氢罐以及氢负荷。HRS以购电成本最小化为目标,根据IES制定的电价作出响应,调整自身的购电策略,同时利用分布鲁棒处理氢气负荷需求的不确定性。
1.2 能量博弈交互过程
在IES – HRS联合运行的框架下, IES运营商作为领导者,优化向HRS的售电电价和系统调度计划,使得运营成本最小化;HRS作为电能需求侧的参与者,扮演跟随者角色,根据IES的价格信号,优化购能计划和运行计划,以实现最小化购能成本。博弈过程分为两阶段。
第一阶段(领导者决策):IES运营商制定电力价格及能源分配策略,并向HRS发布价格信号。在运行阶段,系统面临PV、WT和电热负荷不确定性的威胁。同时,在定价阶段,IES运营商对于这些不确定性信息的了解仅限于对边界的了解。考虑到这一点,将IES运营商的定价问题表述为一个两阶段自适应鲁棒优化模型,以降低决策的保守性。第一阶段变量,即“此时此地”变量,包括电价、充放电状态和购售电计划,它们根据不确定变量的预测信息进行优化,以实现鲁棒性。第二阶段变量,即“观望”(或追索性)变量,包括设备的输出,它们是自适应的,可以在不确定性实现后进行优化。
第二阶段(跟随者响应):HRS根据IES发布的价格信号,优化自身运营策略(如电能采购、氢气制备、存储、销售计划),并向IES反馈需求信息。在HRS运营中,氢气需求量的不确定性是核心挑战之一。为了精确刻画储氢罐内氢负荷的动态变化(如储氢量的实时波动、制氢与耗氢的平衡关系)及其与用户氢负荷需求之间的耦合作用,本文在HRS模型中嵌入储氢罐的动态模型。该模型通过描述储氢罐内氢负荷变化、制氢量、耗氢量以及用户需求的随机性,为系统优化提供物理基础,并且用户氢负荷的波动会影响购能成本。为此,需进一步将HRS的运营问题建模为分布鲁棒机会约束优化模型:在仅已知部分不确定性概率分布信息的条件下,通过设定风险容忍度,在保障系统可靠性的同时,最小化最坏情景下的预期购能成本。这一方法既避免了传统鲁棒优化过于保守的缺陷,又克服了随机规划对精确概率分布的依赖,从而在经济性与鲁棒性之间实现有效权衡。
2 基于 Stackelberg 博弈的双层定价模型
2.1 上层IES两阶段自适应鲁棒优化模型
IES运营商需要考虑源荷不确定性来确定最优的系统调度计划并发布其最优的能源零售价格,以期实现自身的成本的最小化。
2.1.1 目标函数
IES的目标函数为运行成本Copr减去与加氢站交互收入CHRS,其中运行成本Copr包含与主网购售电成本Cgrid、机组燃料成本Cfuel和储能系统退化成本Cbattery。
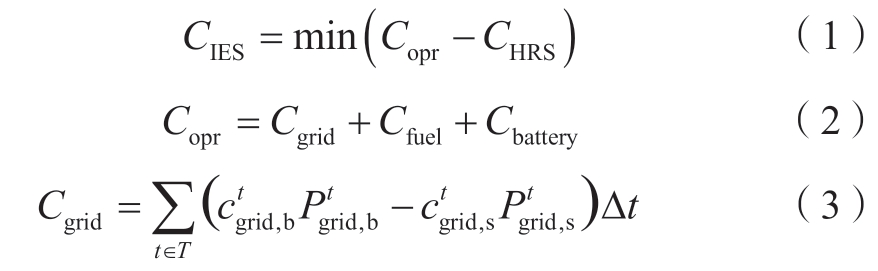
式中:![]() 为电网购/售电价;
为电网购/售电价;![]() 表示购/售电功率;∆t为一个调度时段;t表示t时刻;T是时间t的集合。
表示购/售电功率;∆t为一个调度时段;t表示t时刻;T是时间t的集合。
式中:cgas为单位天然气成本;![]() 表示热电联产机组/燃气锅炉耗气量。
表示热电联产机组/燃气锅炉耗气量。
式中:cbattery为单位充放电成本;![]() 为储能系统充/放电量。
为储能系统充/放电量。
式中:πt为HSR的购电电价;![]() 为HSR的购电功率。
为HSR的购电功率。
2.1.2 约束条件
1)与主网交互购售电约束。
式 (7) 约束了购售电的上下界,式 (8) 表示不能同时购售电。
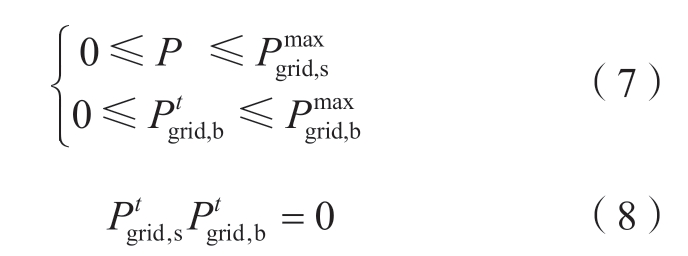
式中:![]() 表示向电网购/售电允许最大值。
表示向电网购/售电允许最大值。
2)储能系统约束。
式 (9) 约束了充放电功率的上下界,式 (10) 表示不能同时充放电。
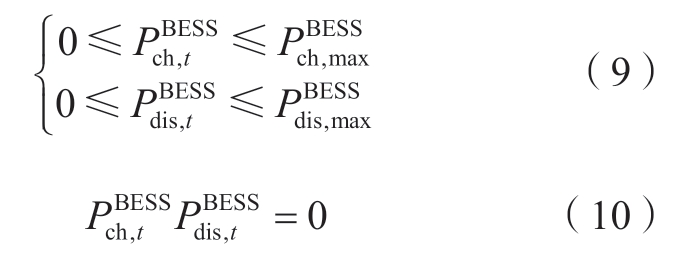
式中:![]() 表示储能充/放电允许最大值。
表示储能充/放电允许最大值。
式 (11) 为充放电状态约束。
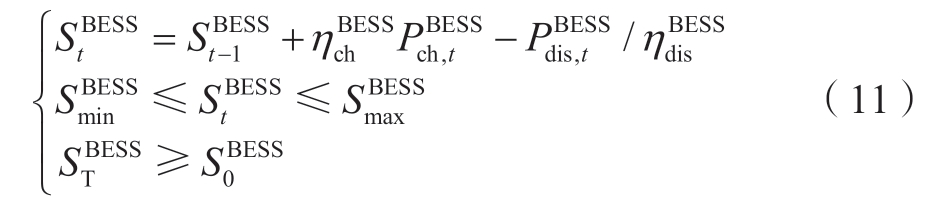
式中:![]() 为储能系统t时刻的荷电状态;
为储能系统t时刻的荷电状态;![]() 表示储能充放电效率;
表示储能充放电效率;![]() 表示储能荷电状态最小值/最大值;
表示储能荷电状态最小值/最大值;![]() 为储能最终荷电状态。
为储能最终荷电状态。
3) CHP运行约束。
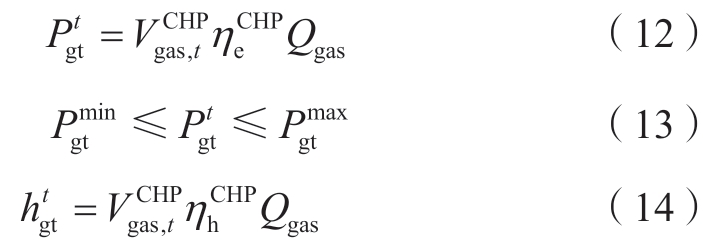
式中:![]() 为热电联产机组的产电量;
为热电联产机组的产电量;![]() 为产电效率;Qgas为天然气热值;
为产电效率;Qgas为天然气热值;![]() 表示机组生产电量的允许最小/最大值;
表示机组生产电量的允许最小/最大值;![]() 为机组产热量;
为机组产热量;![]() 为产热效率。
为产热效率。
4) 燃气锅炉运行约束。
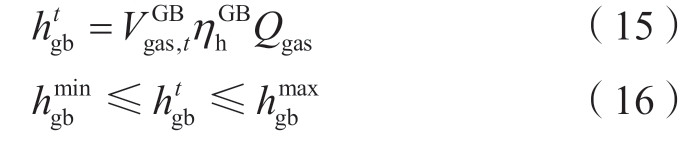
式中:![]() 为燃气锅炉的产热量;
为燃气锅炉的产热量;![]() 为产热效率;
为产热效率;![]() 表示产热量的允许最小/最大值。
表示产热量的允许最小/最大值。
5) 功率平衡约束。
系统运行时电、热功率平衡分别表示为式 (17)和式 (18)。
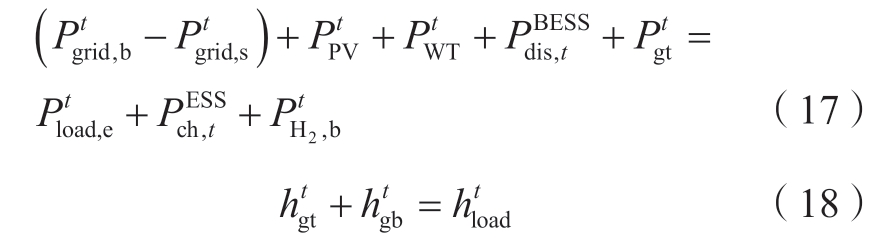
式中:![]() 为考虑不确定性后光伏、风电的功率;
为考虑不确定性后光伏、风电的功率;![]() 考虑不确定性的电、热负荷。
考虑不确定性的电、热负荷。
2.1.3 源荷不确定性建模
风光发电和电热负荷的不确定性影响了IES的运行,这促使IES运营商在确定调度计划和售电价格时谨慎处理。本文采用盒式不确定性集[20]对PV、WT功率和电热负荷进行建模。模型见式 (19)—(26)。约束 (19) 和 (20) 分别定义随机PV和WT功率。约束(21) 和 (22) 分别定义随机电负荷和热负荷。本文分别在 (23) 和 (24) 中定义了PV和WT功率的不确定性集, (25) 和 (26) 中定义了电热负荷的不确定性集。为降低保守性,这里引入鲁棒系数Γ,Γ ∈[0,J],其中J为不确定参数的集合。
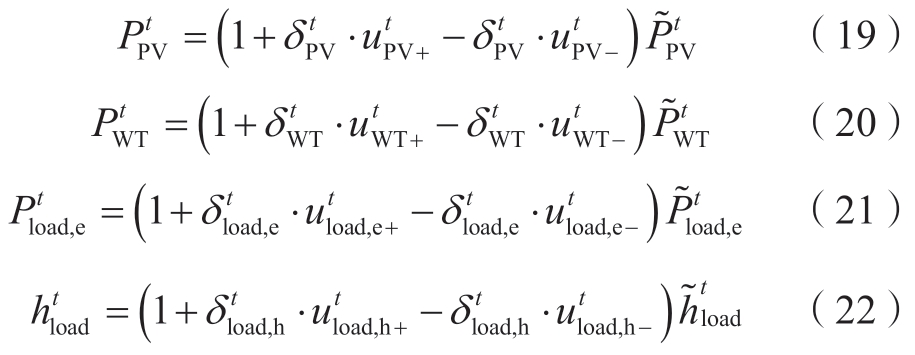
式中:![]() 为PV/WT预测值;
为PV/WT预测值;![]() 为电/热负荷预测值;
为电/热负荷预测值;![]() 为PV/WT功率偏差比;
为PV/WT功率偏差比;![]()
![]() 为电/热负荷功率偏差比;
为电/热负荷功率偏差比;![]() 表示PV功率正/负偏差的随机变量;
表示PV功率正/负偏差的随机变量;![]() 表示WT功率正/负偏差的随机变量;
表示WT功率正/负偏差的随机变量;![]() 表示电负荷正/负偏差的随机变量;
表示电负荷正/负偏差的随机变量;![]() 表示热负荷正/负偏差的随机变量。
表示热负荷正/负偏差的随机变量。
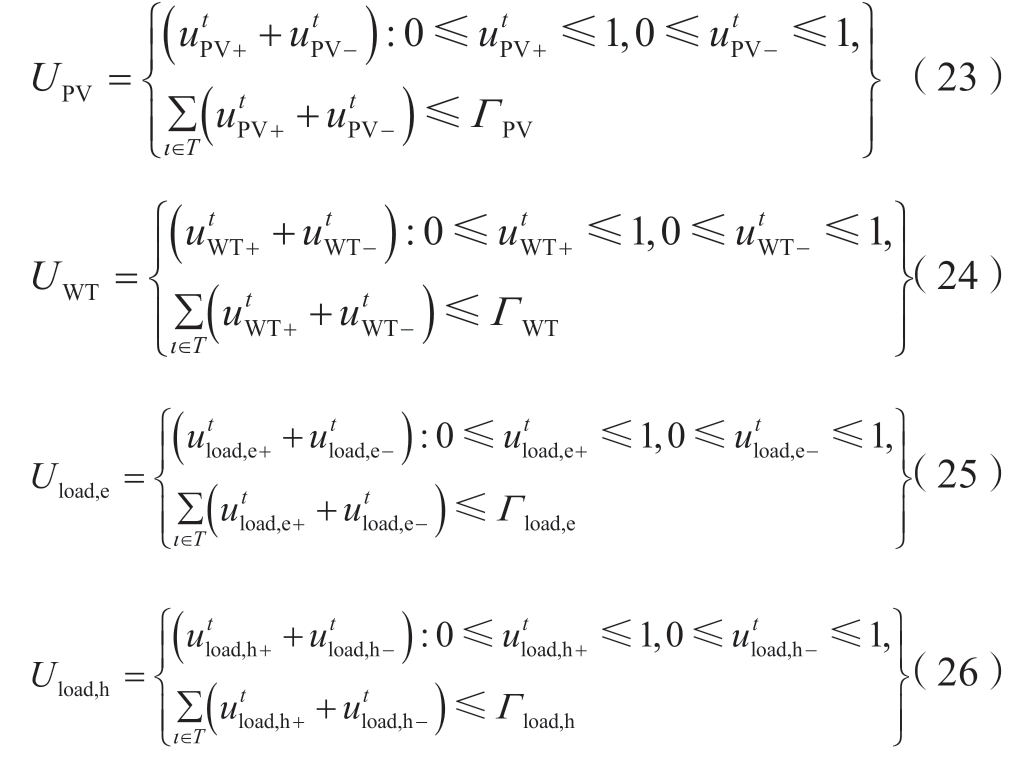
式中:UPV、UWT、Uload,e、Uload,h分别表示光伏出力、风电出力、电负荷、热负荷的不确定性集合;ΓPV、ΓWT、Γload,e、Γload,h分别为光伏出力、风电出力、电负荷、热负荷鲁棒系数。
2.1.4 价格模型
本文价格约束如式 (27) 所示。第一个约束定义了价格的上界和下界,以避免出现极值;第二个约束定义了平均价格不应超过电网分时电价的平均值,使得IES具有市场竞争力。
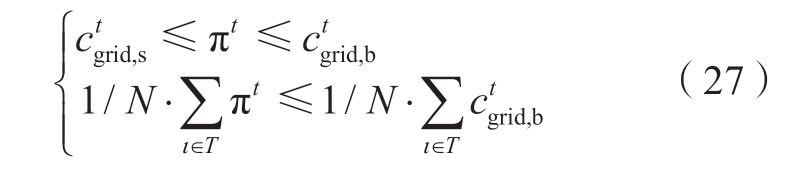
2.1.5 IES紧凑形式
最后,IES运营商模型的紧凑形式被定义为式(28) —(32)。
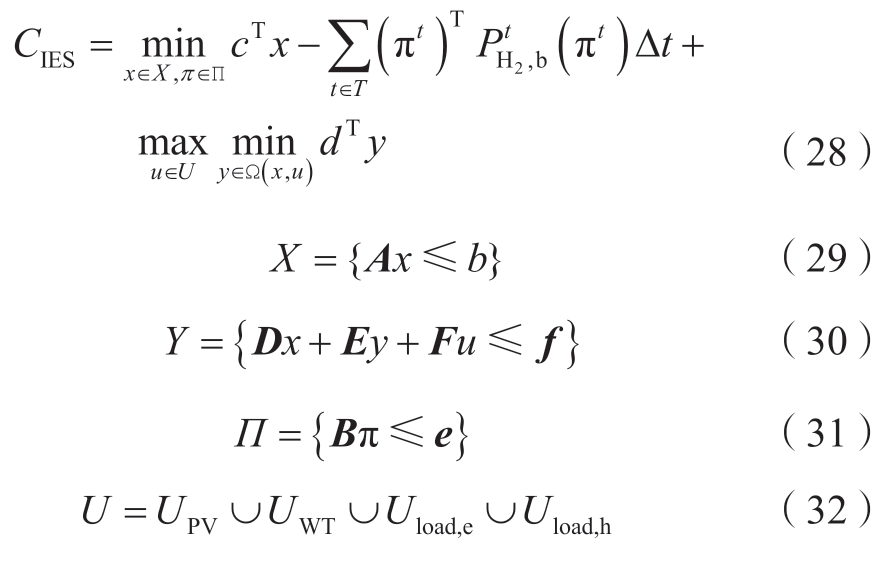
式中:A,B,D,E,F分别为常数矩阵;b,e,f为常数向量;x表示第一阶段决策变量集合;X是第一阶段相关约束构成的可行域;π表示HSR的购电电价变量集合;Π是HSR的购电电价相关约束构成的可行域;u表示第二阶段的不确定性变量;U是不确定集合;y表示第二阶段的决策变量集合;Ω是第二阶段相关约束的可行域。
2.2 下层加氢站DRCC优化模型
HRS跟随 IES制定的电价,通过用户的氢负荷需求调整自身购电和运行计划。以自身购能成本最小化为原则,采用DRCC刻画氢负荷需求的不确定性,实现HRS经济安全运行。
2.2.1 目标函数
HRS的成本函数可以表示为
2.2.2 约束条件
1) 氢负荷约束。
本文使用随机变量![]() 对氢负荷需求
对氢负荷需求![]() 的不确定性进行建模,如式 (34)所示。
的不确定性进行建模,如式 (34)所示。
式中:![]() 分别为考虑不确定性后/预测氢负荷;
分别为考虑不确定性后/预测氢负荷;![]() 为氢负荷t时刻偏差的随机变量。
为氢负荷t时刻偏差的随机变量。
为了捕捉氢负荷的不确定性,本文利用随机变量ξH2的一阶矩和二阶矩信息[21],构造了模糊集PH2(ambiguity set):
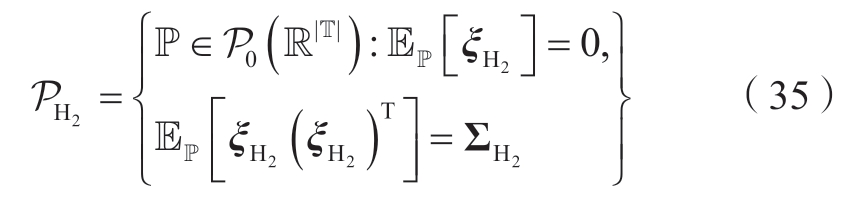
式中:PH2为氢负荷的模糊集;ξH2表示氢负荷偏差向量;ΣH2为随机变量ξH2协方差矩阵。
2)储氢罐运行约束。
充放氢状态约束可以表示为式(36)。
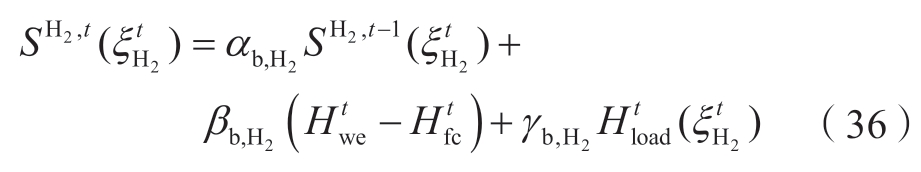
式中:![]() 为t时刻储氢罐状态变量;
为t时刻储氢罐状态变量;![]() 为t时刻的产/耗氢量;αb,H2、βb,H2、γb,H2储氢罐运行系数。
为t时刻的产/耗氢量;αb,H2、βb,H2、γb,H2储氢罐运行系数。
为保证储氢罐储氢量应在合理的范围内变化[22]。考虑到氢负荷的随机性,本文使用机会约束来模拟储氢罐氢气量的变化,如式 (37) 所示。
式中:![]() 为储氢罐储氢的理想值;∆SH2为储氢罐储氢的波动范围;∊H2为储氢罐储氢量约束的置信水平。
为储氢罐储氢的理想值;∆SH2为储氢罐储氢的波动范围;∊H2为储氢罐储氢量约束的置信水平。
此外,储氢罐平均储氢量应等于理想值,以避免储氢罐过度充氢带来的安全问题和过度放氢造成的资源闲置浪费,如式 (38)所示。
3) P2H/H2P设备运行约束。
P2H设备制氢约束如式 (39) 所示。
式中:![]() 为t时段产生的氢气量;
为t时段产生的氢气量;![]() 为t时段的电解功率;ηP2H为电转氢效率;αP2H为P2H设备运行系数。
为t时段的电解功率;ηP2H为电转氢效率;αP2H为P2H设备运行系数。
H2P设备产电约束如式 (40) 所示。
式中:![]() 为t时段的输出电功率;
为t时段的输出电功率;![]() 为t时段消耗的氢气量;ηH2P为氢转电效率;αH2P为H2P设备运行系数。
为t时段消耗的氢气量;ηH2P为氢转电效率;αH2P为H2P设备运行系数。
P2H/H2P设备功率上下限约束如式 (41) 所示。
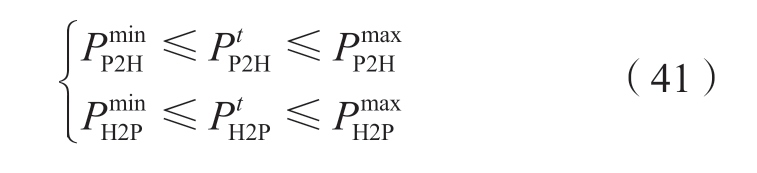
式中:![]() 分别为P2H设备运行功率的下限/上限;
分别为P2H设备运行功率的下限/上限;![]() 分别为H2P设备运行功率的下限/上限。
分别为H2P设备运行功率的下限/上限。
4) HRS购电约束。

2.2.3 确定性等价
本节将HRS的DRCC优化模型转化为等效的确定性形式。
引入一个新的变量![]() 来表示预测氢负荷
来表示预测氢负荷![]() 下的储氢罐状态,如式 (44) 所示。然后令
下的储氢罐状态,如式 (44) 所示。然后令![]() ,由式(36)可以得到式(45)。
,由式(36)可以得到式(45)。
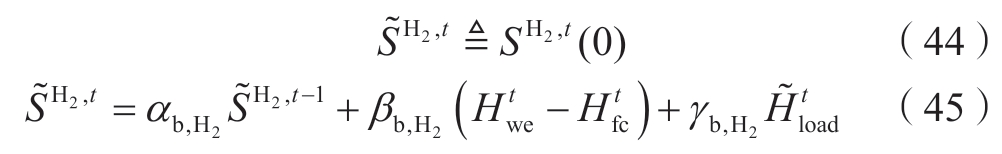
进一步,约束 (37) 和 (38) 可以分别重新表述为约束式 (46) 和式 (47)。
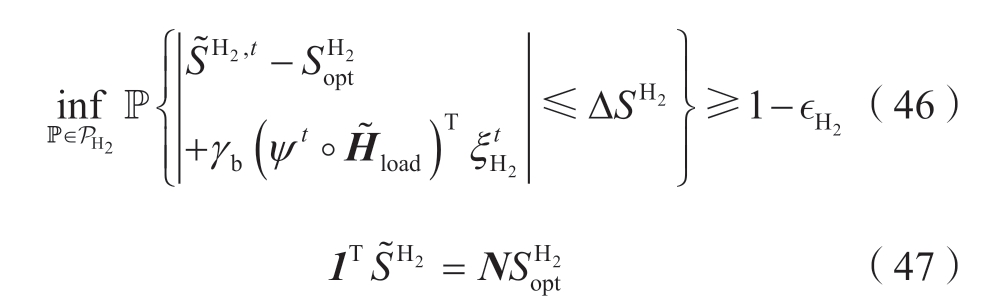
式中:◦为哈达玛积;ψt是一个常数向量,定义为式 (48)。
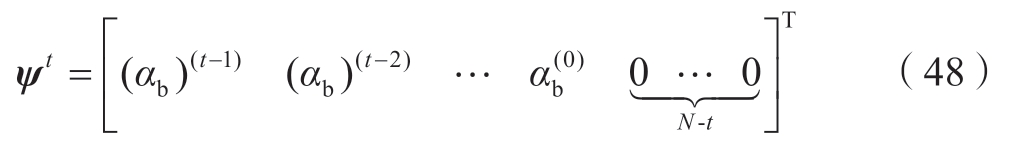
约束(46)和(47)详细推导见附录A。
根据命题1约束 (46) 可以进一步转化为线性约束。
命题1:在模糊集 (35) 下,分布鲁棒机会约束(46)等价于以下线性约束
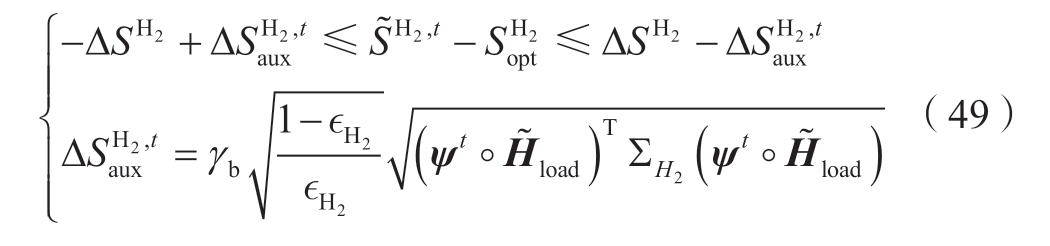
式中:![]() 为辅助参数;
为辅助参数;![]() 。
。
命题1的证明见附录A。
到此为止,HRS的DRCC优化模型可以转化为由(33)、(39)、(40)、(41)、(42)、(43)、(45)、(47)、(49)组成的确定性模型。
2.2.4 紧凑形式
HRS的紧凑形式见式(50)—(51)。决策变量包括购电量、产氢量、耗氢量、电转氢/氢转电功率。

式中:z为下层决策变量;Zprimal为下层问题可行域;G1、G2、G3为常数矩阵;g为常数向量;![]() 为初始储氢罐状态矢量;λi、μi为对偶乘子。G1、G2、G3、g和S~H ,02 的取值见附录B。
为初始储氢罐状态矢量;λi、μi为对偶乘子。G1、G2、G3、g和S~H ,02 的取值见附录B。
3 模型求解
本章首先证明该模型下Slater条件的成立,然后基于KKT条件、大M法和强对偶理论将模型线性化,实现模型的可求解。
3.1 模型的紧凑形式
结合IES运营商和HRS的模型,本文提出的定价模型如式(52)所示。
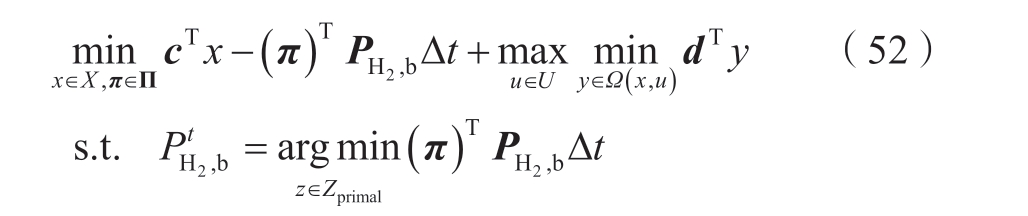
3.2 模型求解
文献[23-24]指出,当双层优化问题中的下层优化问题为凸问题,则能够通过KKT最优性条件进行转化时,该双层优化问题与转化后的单层数学规划模型(mathematical program with equilibrium constraints,MPEC)是等价的。转化后的MPEC问题存在非线性约束,可通过引入0-1变量和正常数M,即大M法,进行线性转化[25-26]。因此,为了求解该定价模型,下面基于KKT条件和大M方法,将HRS模型 (50)—(51)转化为混合整数线性约束。然后,将定价模型重新表述为经典的TSRO问题。
命题2:当且仅当下列条件成立时,模型 (50)—(51) 的Slater条件成立:
证明过程见附录A。
基于命题2,HRS模型具有强对偶性。因此,可等价于KKT条件[26],为式(54)—(56)。

式中:Zopt是最优性条件;Zcomp是对偶可行条件和互补松弛条件。
式 (56) 中的约束为互补约束,其中x,y表示x≥0,y ≥0,xy=0。基于大M方法,互补约束可以线性化为式(57)。

式中:κ是一个大常数。
综上所述,HRS模型被等效为混合整数线性约束。进一步,基于强对偶定理[27-28],在式 (52) 中的双线性项( π) T PH ,b2可以等价地重新表述为函数f,如式 (58)所示。
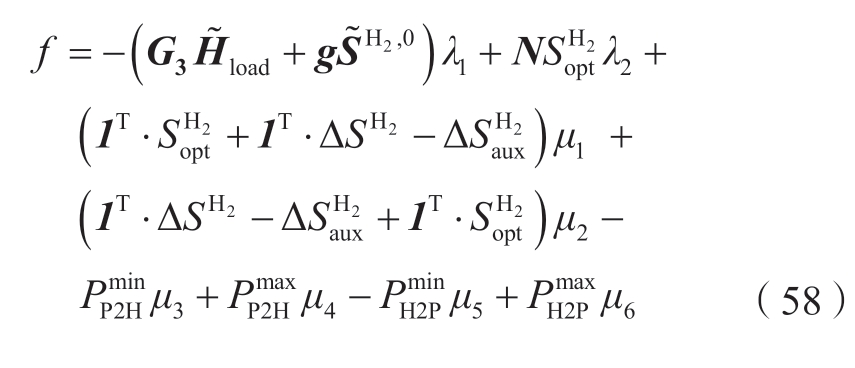
基于式 (54)—(58),模型 (52) 可以转化为经典的TSRO模型,即
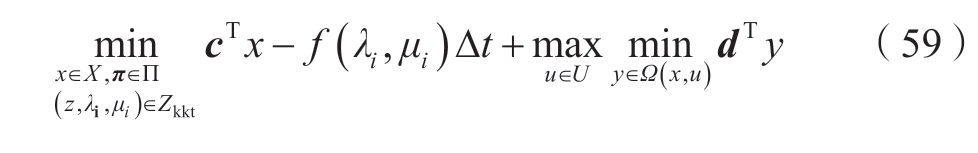
在该模型中,第一阶段问题具有凸二次目标函数和整数连续决策变量,第二阶段问题具有线性目标函数和连续决策变量。该模型可通过著名的C&CG方法高效求解[29]。
4 算例分析
4.1 参数设置
本节以图1所示的北方某地区综合能源系统和加氢站一天的运行情况为例进行了讨论分析,调度时间间隔为1 h。本文在第12代Intel酷睿i5环境下的微型计算机上通过MATLAB2022b使用YALMIP工具箱调用GUROBI求解器进行求解。
对外网购电和售电的电价,以及天然气公司购气价格,如附录B图B1所示。能量转换装置、存储装置、效率和运行限值参数如表B1所示[30-31]。IES的负荷和可再生能源出力预测曲线,以及HRS氢负荷预测曲线如图B2所示。源荷作为系统中的不确定因素,其不确定性分别为预测值的15%和10%波动[32]。
4.2 算法收敛性分析
C&CG算法的收敛过程如图2所示。可以看出,C&CG算法具有快速收敛的特性,经过11.328 s计算,在第2次迭代就达到了收敛,具有非常良好的性能。
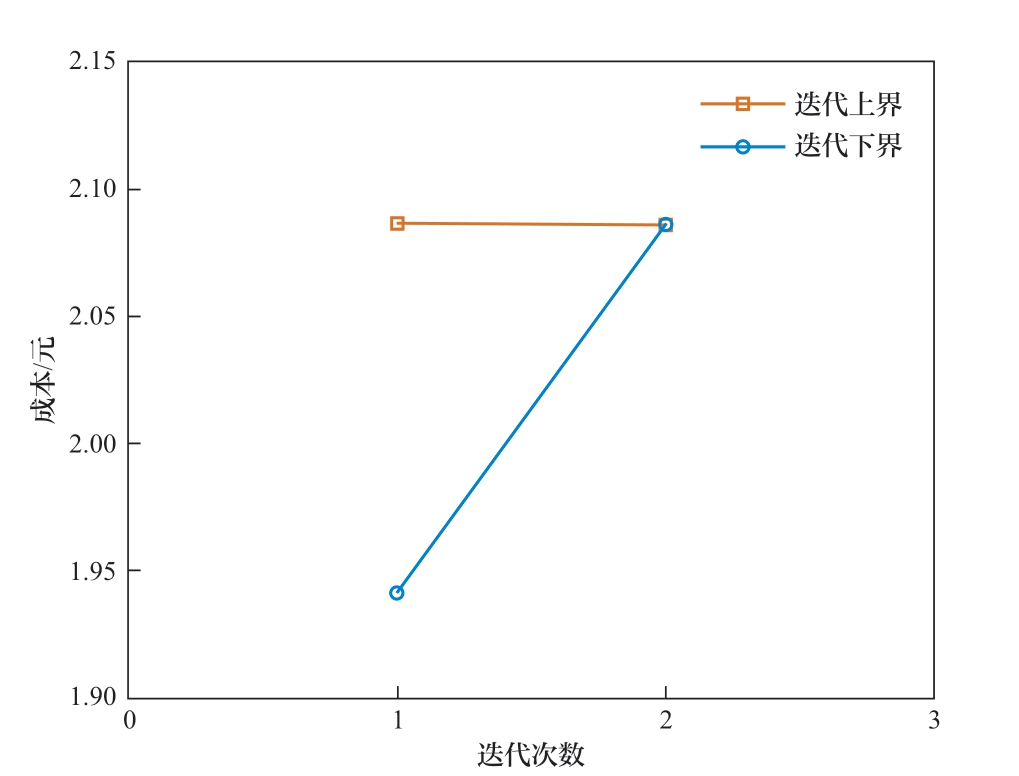
图2 模型收敛过程
Fig. 2 Model convergence process
4.3 能量交互和定价结果分析
各能源主体之间的能源交换对提高整个系统的效率至关重要,因为它不再仅仅依赖于它们各自的供应能力。在一个能量不足的系统中,能量可以从能量充足的系统中购买。IES一天的电力和热力调度情况受负荷水平、能源价格、多能匹配程度等因素影响。图3和图4分别IES展示了电力和热力调度。由图3可知,IES在一天中频繁向电网购电,大量购入的时段多数处于电价中低位时段。造成这一情况的原因主要有2个:一是产热联产机组的出力耦合导致电力交互量不仅仅取决于电力负荷需求,还需要兼顾热力负荷需求;二是电价远低于天然气价格,IES会尽量避免CHP与燃气锅炉同时运行。综合图3和图4的信息可知,1:00—5:00这个时段,CHP没有出力,热负荷是由燃气锅炉提供,电负荷是通过向电网买电进行满足。在10:00—18:00这个时段,燃气锅炉没有出力,CHP在优先满足热负荷的情况输出电功率,电量需求与CHP电功率出力的缺口通过向电网买电进行满足。
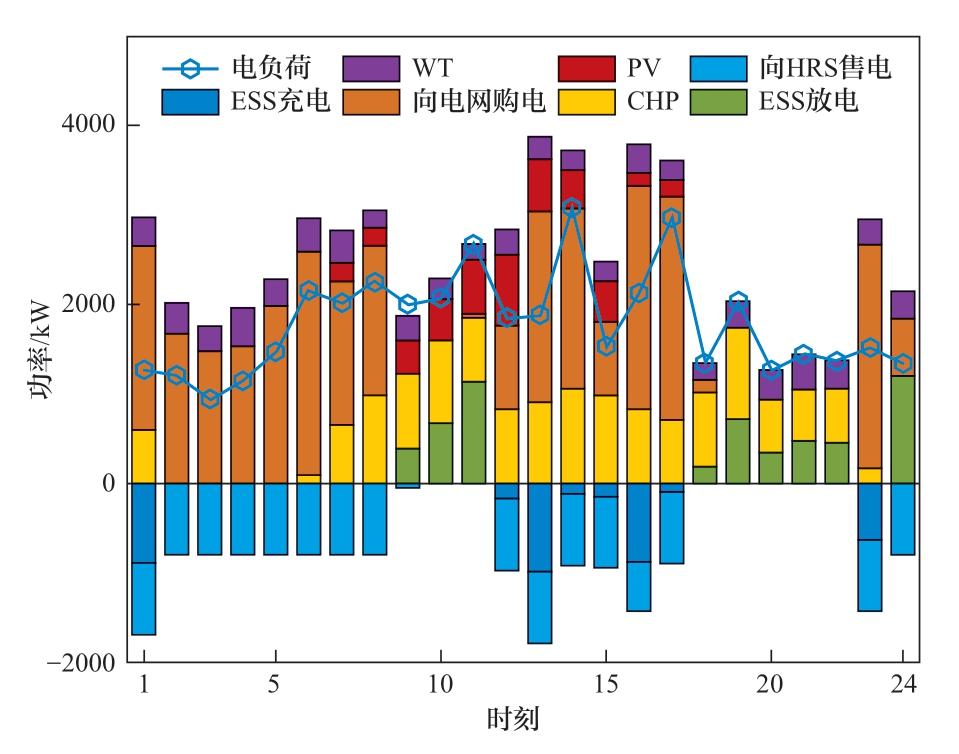
图3 IES电力调度示意图
Fig. 3 Schematic diagram of IES power dispatch
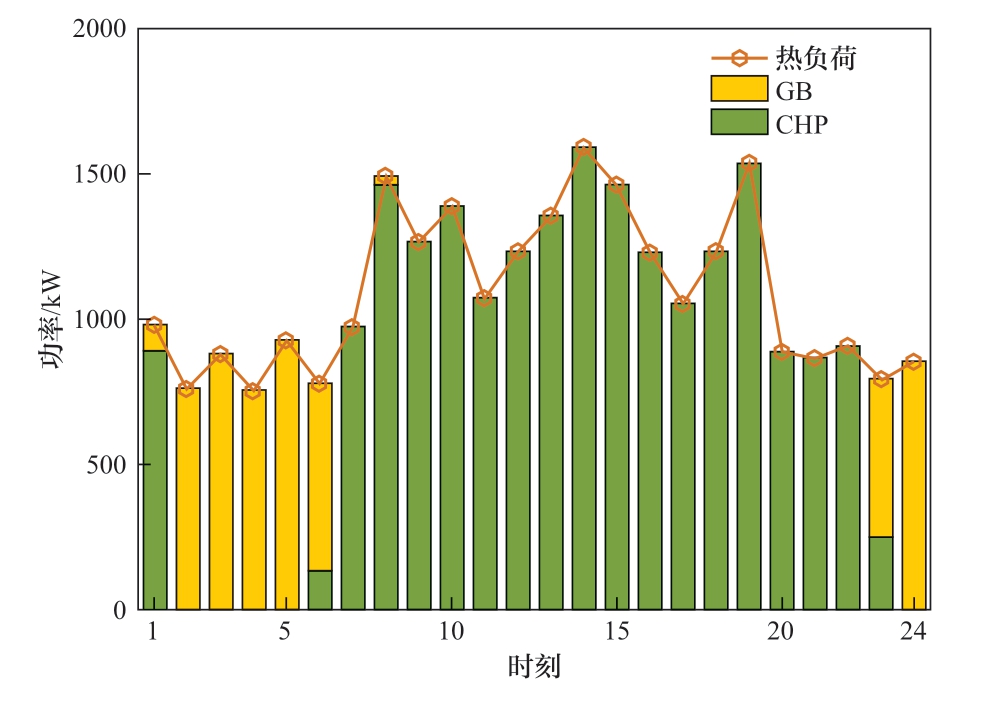
图4 IES热力调度示意图
Fig. 4 Schematic diagram of IES heat dispatch
图5显示了IES对HRS制定的电价策略。图5中,紫色虚线和黄色虚线分别为电网提供的上网电价和分时电价。IES在这个范围内,经过双方不断的博弈,提供了比电网分时电价更优惠的价格。同时,因为给HRS制定的电价高于上网电价,所以IES多余的电量会与加氢站交易而不会选择上网。结合图3和图5可以发现,加氢站会在0:00—8:00、11:00—15:00、16:00—17:00和22:00—24:00这4个低电价时段大量向IES买电,在8:00—9:00和15:00—16:00这2个高电价时段根据需求少量买电,从而实现自身购电成本的最小化。从图6以得出,0:00—6:00和22:00—24:00这2个时段大量购电是低成本制氢进行氢气囤积,6:00—8:00、11:00—15:00和16:00—17:00这3个时段大量购电是因为大量的氢负荷需求和制氢成本低。本文所提的定价策略可以在保证供能平衡的前提下,实现了促进IES与HRS利益最大化的共赢。
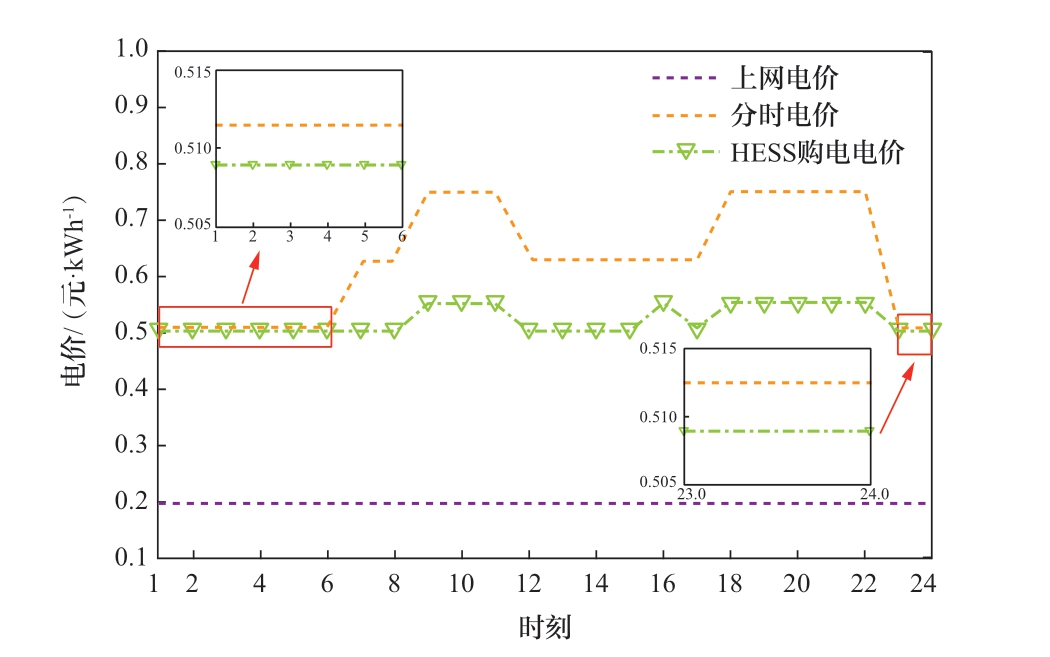
图5 IES和HES的交互电价
Fig. 5 Interactive tariffs of IES and HES
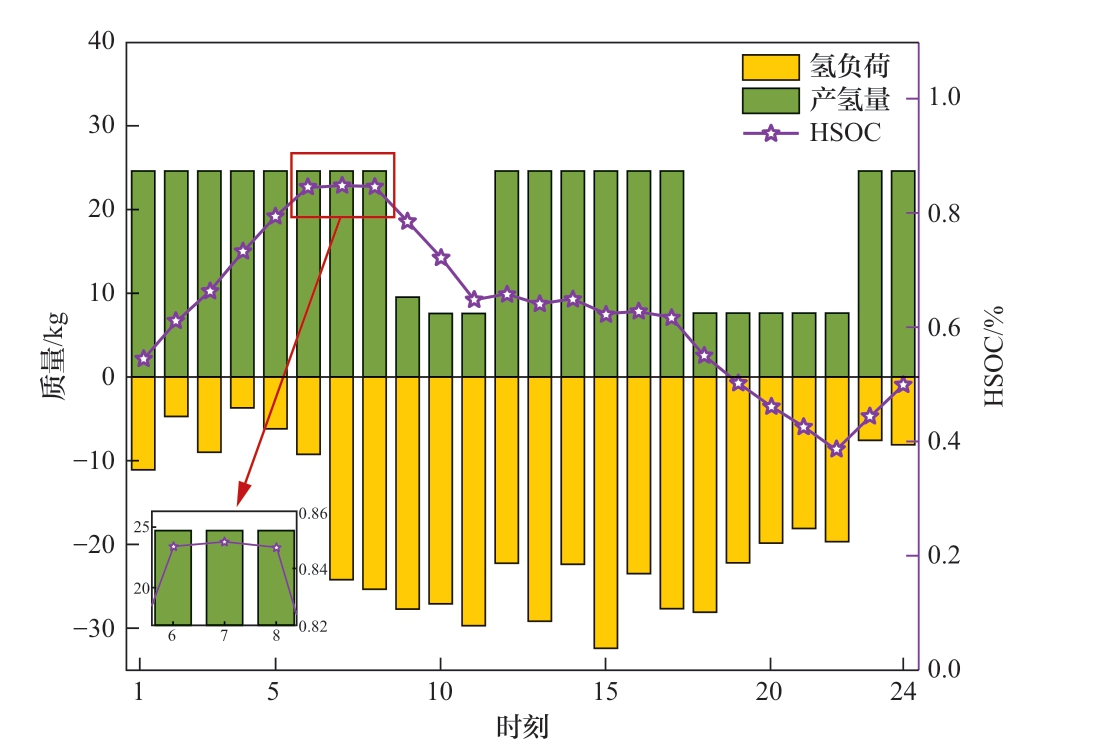
图6 加氢站供需量及储氢罐状态示意图
Fig. 6 Operation of hydrogen refueling stations
4.4 定价策略对比
本节比较了确定性博弈定价和所提鲁棒博弈定价策略对优化结果的影响。从表1可以看出,与确定性博弈定价方法相比,本文提出的模型考虑了IES面临的源荷波动和HRS面临的氢负荷波动等多重不确定性。虽然鲁棒博弈方法中IES运营商在燃料成本、储能退化成本、与电网交互成本以及与HRS交互成本等方面都有小幅增长,总运营成本增加了1 435.034元,HRS的购能成本增加了281.912 4元,但这不意味着确定性博弈定价方法优于鲁棒定价方法,这是由于确定性方法根据历史信息进行预测后展开调度,未考虑预测误差带来的不确定性风险以及因此导致的再调度成本。由图7和图8可知,在考虑不确定性存在的情况下,风光出力减少且电热负荷需求增大,若按照确定性场景进行调度会出现的供需能量缺口累计3 850.25 kW。再调度需要更多的与上级电网购售电来平抑预测误差带来的功率不平衡,增加实际调度成本2 388.60元。本文提出的鲁棒主从博弈定价方法考虑了多重不确定性,采取较为保守的交易策略,可以降低系统的调度成本和负荷损失,更好地满足系统的能源供应需求。
表1 不同定价策略的成本对比
Table 1 Cost comparison of different pricing strategies
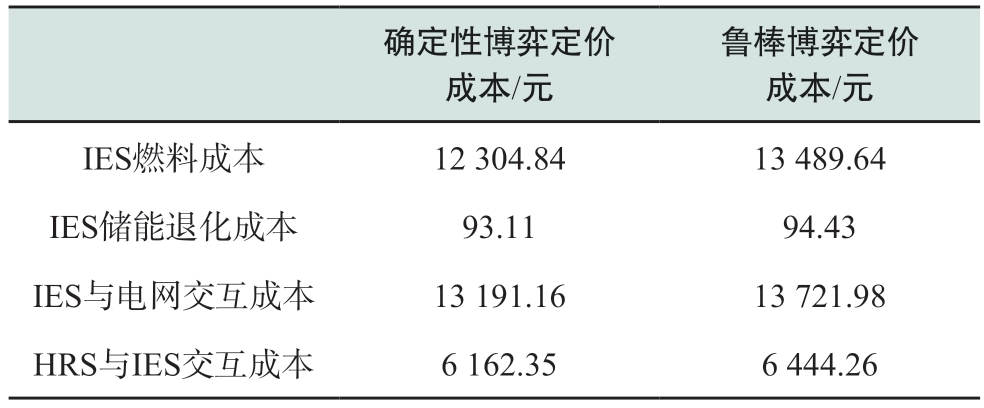
鲁棒博弈定价成本/元IES燃料成本 12 304.84 13 489.64 IES储能退化成本 93.11 94.43 IES与电网交互成本 13 191.16 13 721.98 HRS与IES交互成本 6 162.35 6 444.26确定性博弈定价成本/元
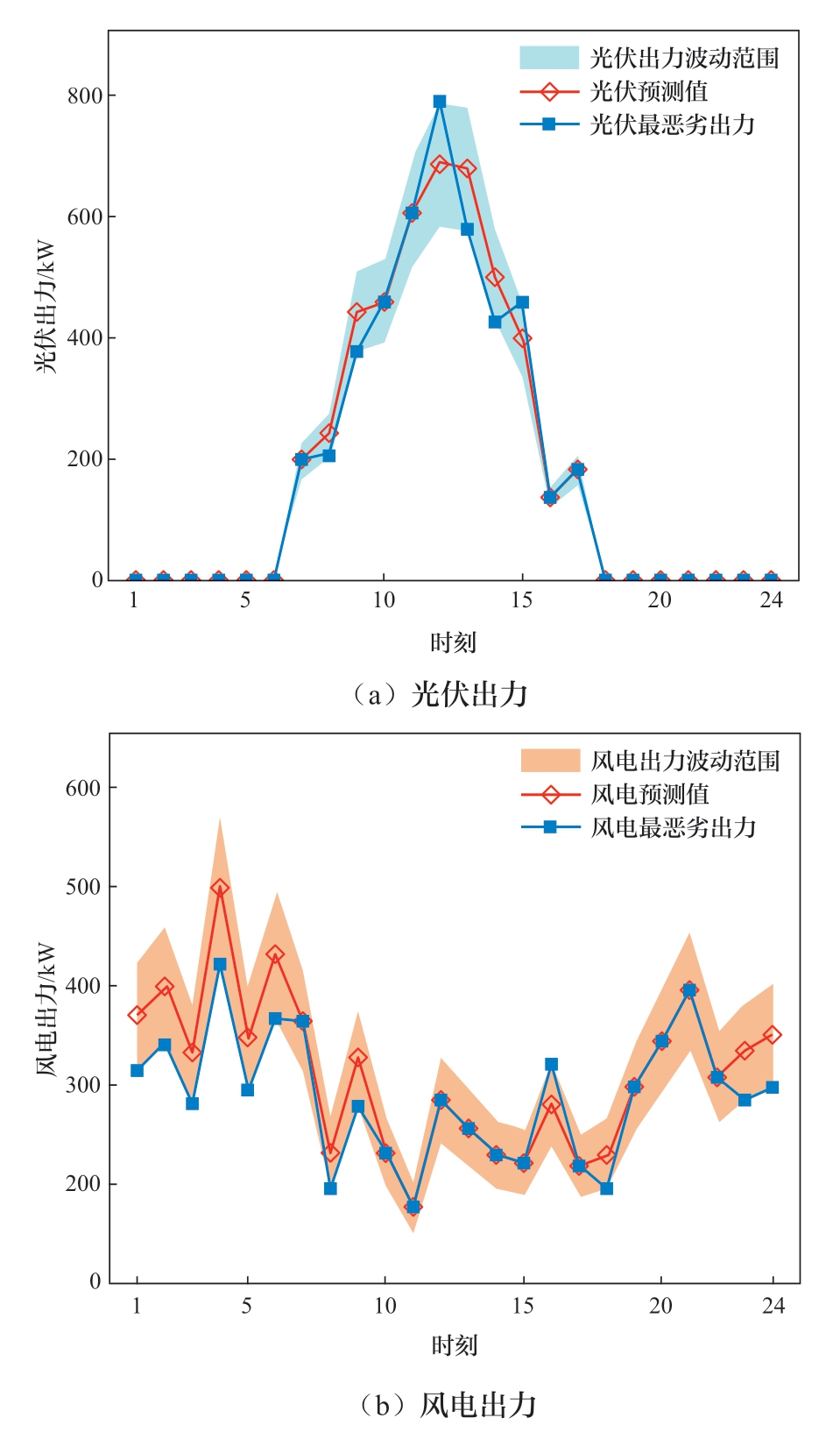
图7 可再生能源出力示意图
Fig. 7 Renewable energy output
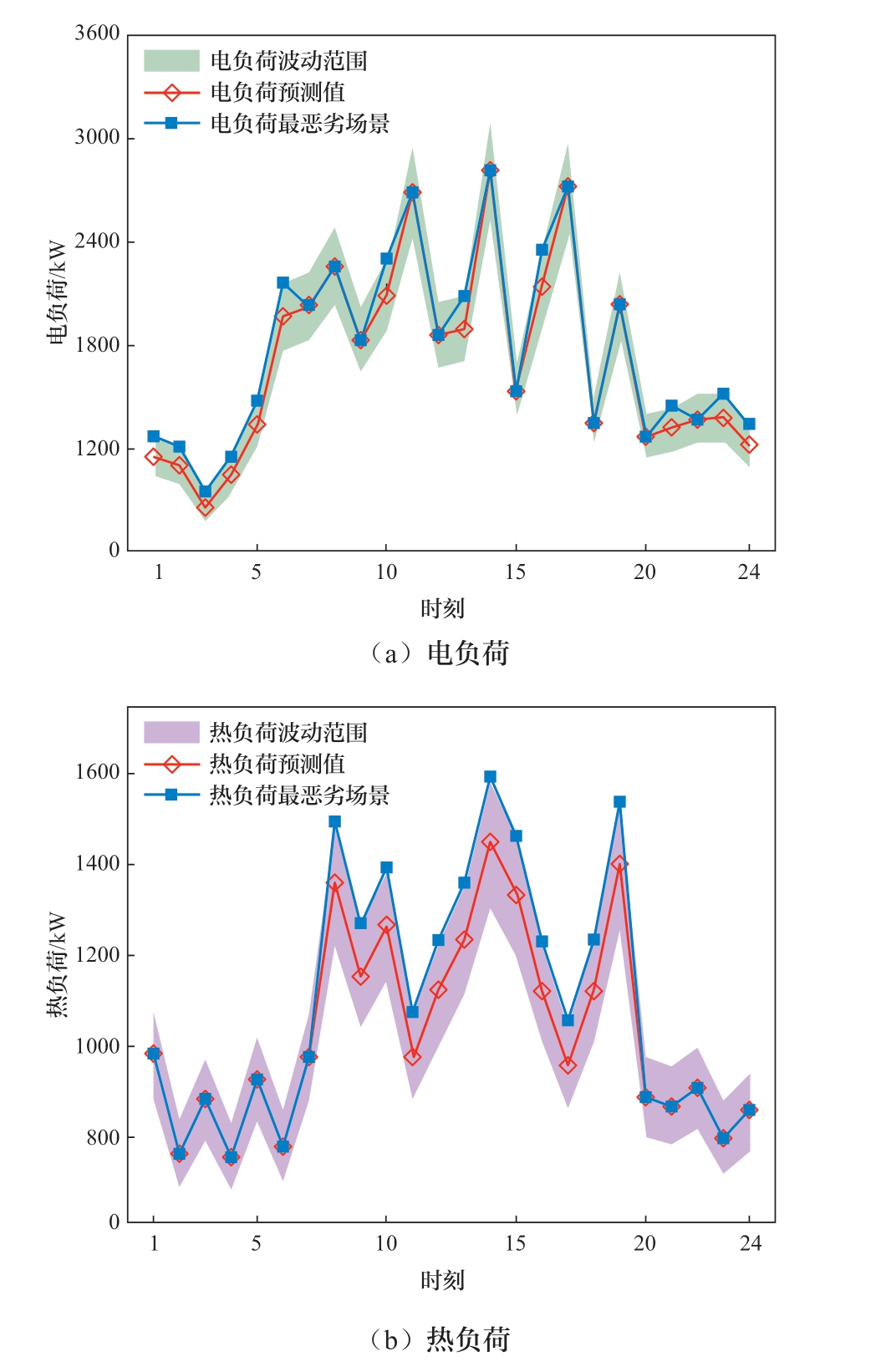
图8 电热负荷波动示意图
Fig. 8 Electricity and heat load fluctuations
4.5 联合运行对比
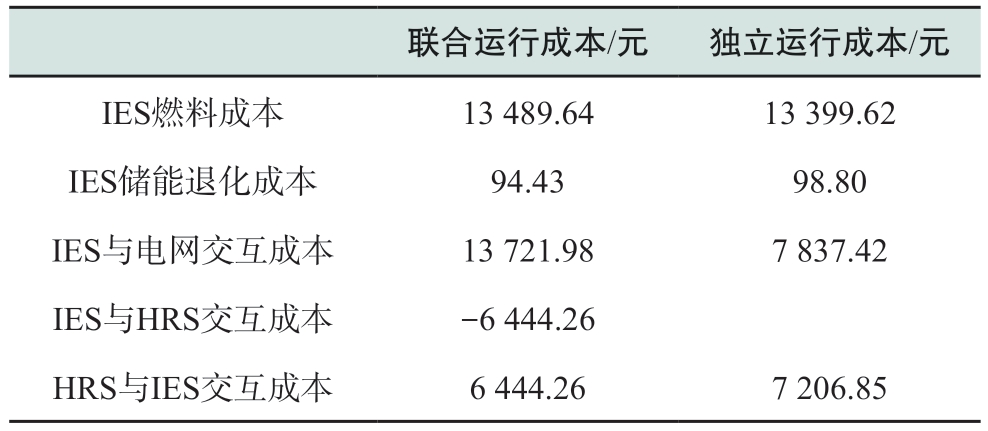
本节对比IES与HRS是否联合运行对自身运行成本的影响,各主体的运行成本对比如表2所示。从表中可以看出,联合运行会降低两者的运行成本,提高两者的运行经济性。联合运行下HRS与IES的能源交易更高效,通过减少与电网的交互享受与IES的优惠定价节约购能成本762.59元。同时,IES的总运行成本会降低474.04元。尽管联合运行时IES的燃料成本和与电网交互成本分布增加了90.02元和5 884.56元,但这是由于联合运行模式下IES因能源协同调度需要以支持HRS需求,导致燃料消耗增加和交互成本上升。IES联合运行储能退化成本减少了4.37元,通过协同优化减少了储能设备的充放功率,从而延缓了性能退化。在联合调度下,IES与HRS的能源互补,使用更合理性,降低了总成本,可见本文提出的定价模型有利于实现二者双赢的局面。
表2 不同运营模式的成本对比
Table 2 Cost comparison of different operating models
联合运行成本/元 独立运行成本/元IES燃料成本 13 489.64 13 399.62 IES储能退化成本 94.43 98.80 IES与电网交互成本 13 721.98 7 837.42 IES与HRS交互成本 -6 444.26 HRS与IES交互成本 6 444.26 7 206.85
4.6 鲁棒性分析
4.6.1 分析确定性与鲁棒性的决策
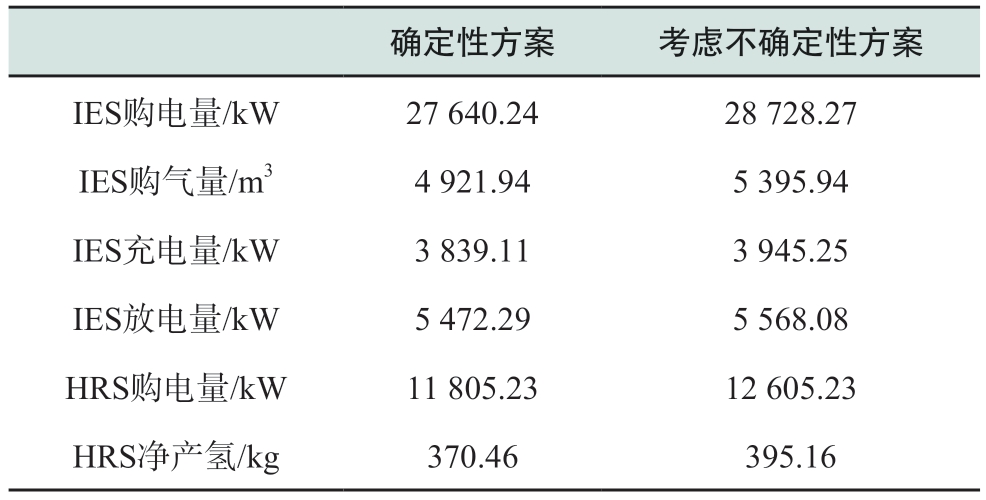
本节将IES的购能计划和充放电计划以及HRS的购能计划与确定性场景进行比较,对比如图9—图12所示,变化量都是考虑不确定性场景与确定场景相应指标之差。IES可以利用直接购气、电和充放电来缓解因源荷波动引起的电力失配问题。由表3可知,与确定性方案相比,系统的电力采购和天然气采购分别增加了1088 kW和474 m3,充电量增加了106.14 kW,放电量增加了95.79 kW,且由图10可知储能系统的SOC变化相较确定场景更加频繁,进一步提高了能源调度计划的保守性。与确定性情景相比,HRS为应对氢负荷的波动,采用了较为保守的购能策略,增加了800 kW的与IES电能交互进行制氢囤积,净产氢增加了24.7 kg,并且由图11可知,在考虑不确定性的情况,HRS增多了在低电价时的购电量,减少了在高电价时的购电量,由图12可知,在考虑不确定性的情况下,HRS会在低电价的时刻增加制氢量使HSOC较确定场景提前达到峰值。
表3 不同方案运行对比
Table 3 Comparison of the operation for different scenarios
确定性方案 考虑不确定性方案IES购电量/kW 27 640.24 28 728.27 IES购气量/m3 4 921.94 5 395.94 IES充电量/kW 3 839.11 3 945.25 IES放电量/kW 5 472.29 5 568.08 HRS购电量/kW 11 805.23 12 605.23 HRS净产氢/kg 370.46 395.16
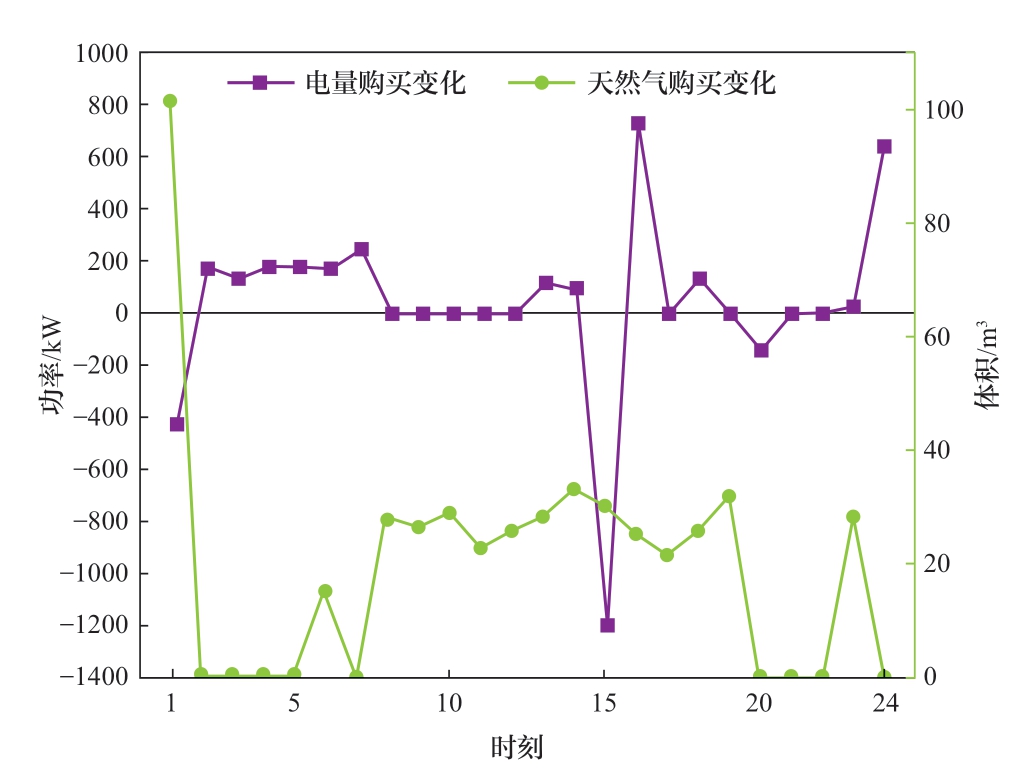
图9 IES购能变化情况
Fig. 9 Changes in IES energy purchase
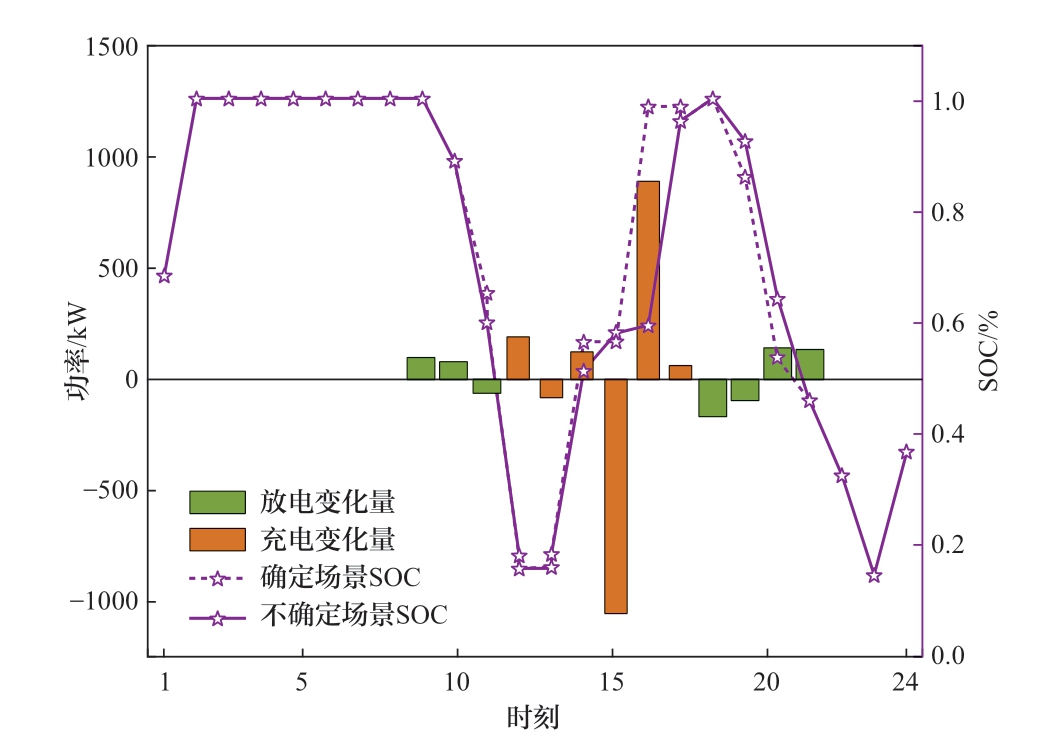
图10 IES充放电变化情况
Fig. 10 Changes in IES charge and discharge
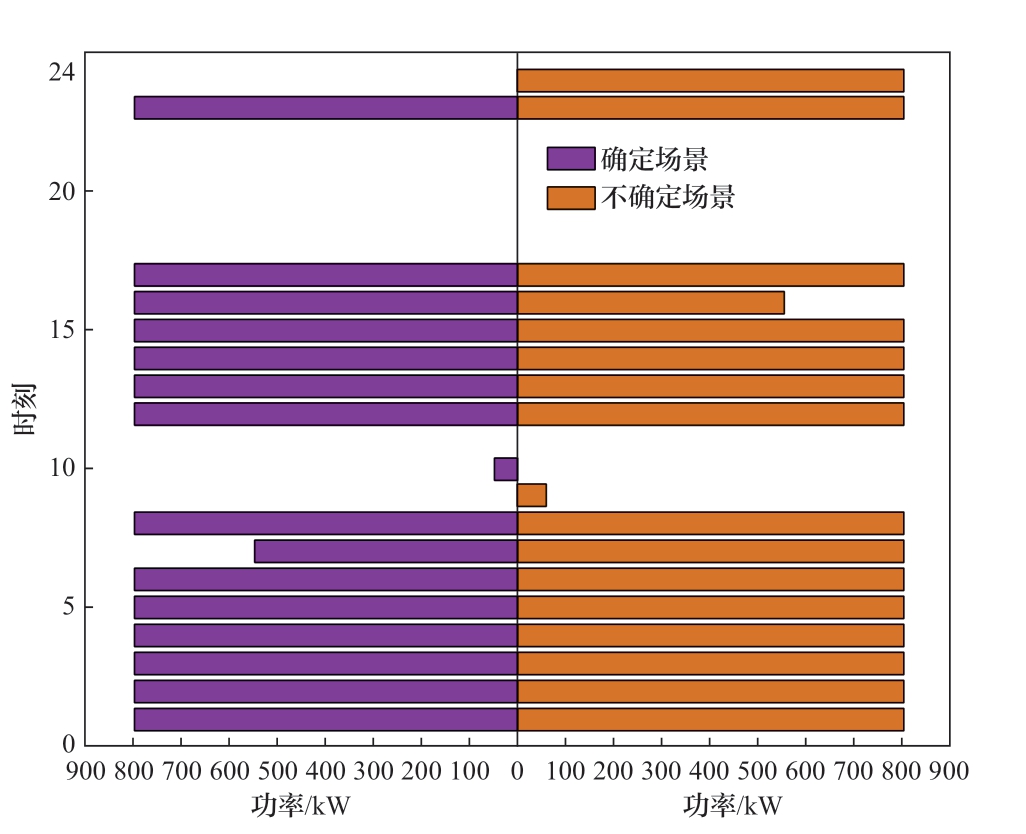
图11 HRS购电情况对比图
Fig. 11 Comparison of HRS power purchase
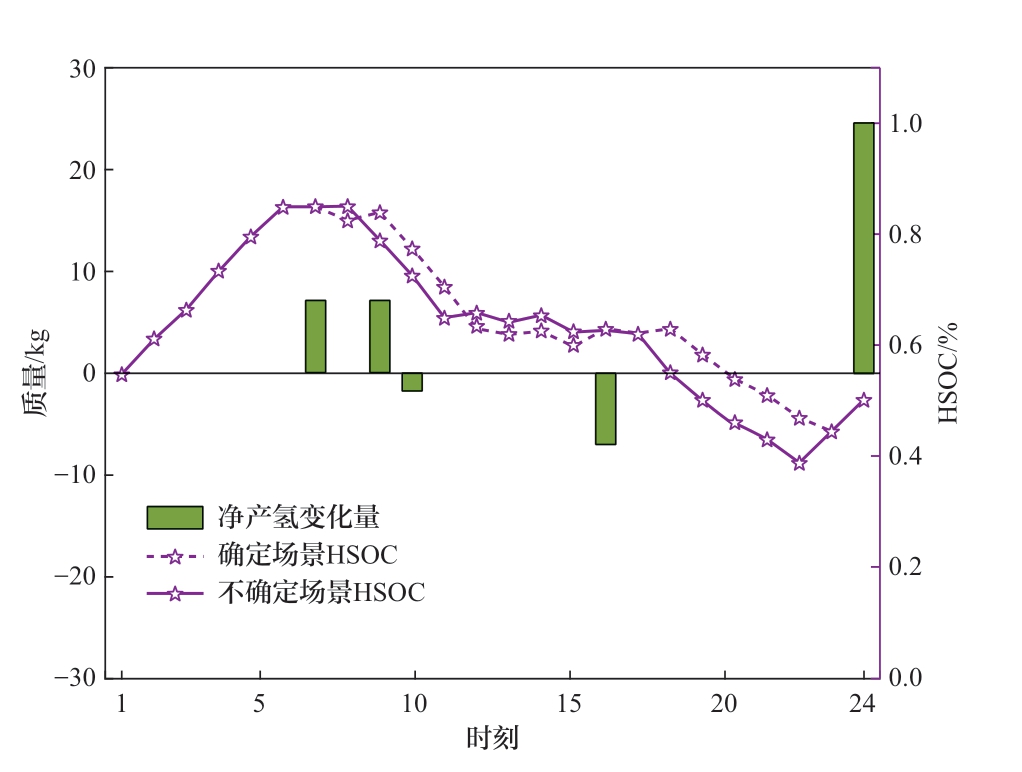
图12 HRS产氢情况对比图
Fig. 12 Comparison of hydrogen production in HRS
4.6.2 敏感性分析
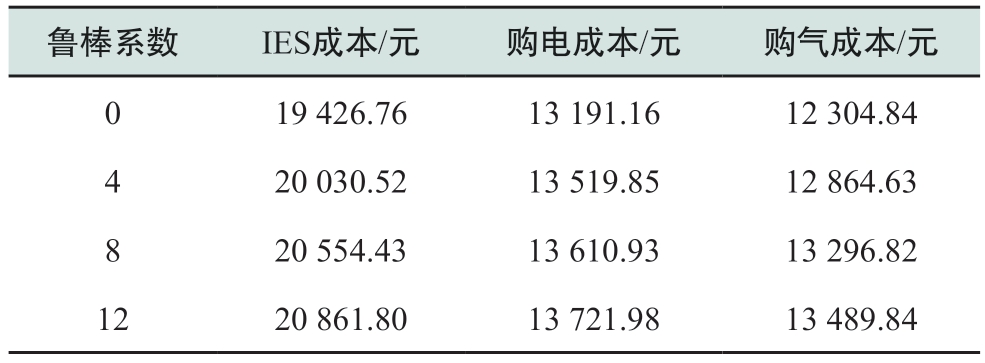
采用多工况仿真方法对源荷不确定性的鲁棒参数和储氢罐储氢量约束的置信水平进行了敏感性分析。鲁棒参数Γ的值越大,决策的保守性越强。为分析可再生能源出力和负荷的不确定性对运行优化的影响,将不确定性水平分别设置为0、4、8、12[20],模拟不同的风光出力和负荷变动对系统运行的影响。不同的鲁棒参数相应的运行成本见表4,从中可以看出,运行成本与不确定比呈正相关。这反映了不确定参数对鲁棒调度计划的影响。当鲁棒参数为0时,与确定性优化结果相对应,系统成本最低,但这种高回报伴随着高风险。随着不确定比率的增加,由于考虑更多不确定的时间段,成本继续上升。系统更多的外部交互提高了能源供应的可靠性。当鲁棒系数为12时,风险较小,但运行成本较高。由此可见,实现低风险需要大量的投资。实际中鲁棒系数的制定可以根据当时运行中对风险偏好的程度进行选择。在HRS分布鲁棒机会约束优化中,置信度是模型的核心参数,其变化直接影响模型的鲁棒性和经济性。为分析储氢罐储氢量约束的置信水平对HRS成本的影响,将置信度分布设置为65、75、85、95[33]。由图13可知,随着置信度的提高会导致解的保守性增强以及经济性下降。当置信度为95时,系统能够在需求波动最坏情况下仍满足约束,但牺牲了一定的经济性,模型需购入更多电力制备氢气应对不确定性,导致总成本上升;反之,当置信度降低时,解的保守性降低,购买电力减少,总成本下降。
表4 鲁棒系数对IES的影响
Table 4 Impact of robustness coefficients on IES
鲁棒系数 IES成本/元 购电成本/元 购气成本/元0 19 426.76 13 191.16 12 304.84 4 20 030.52 13 519.85 12 864.63 8 20 554.43 13 610.93 13 296.82 12 20 861.80 13 721.98 13 489.84
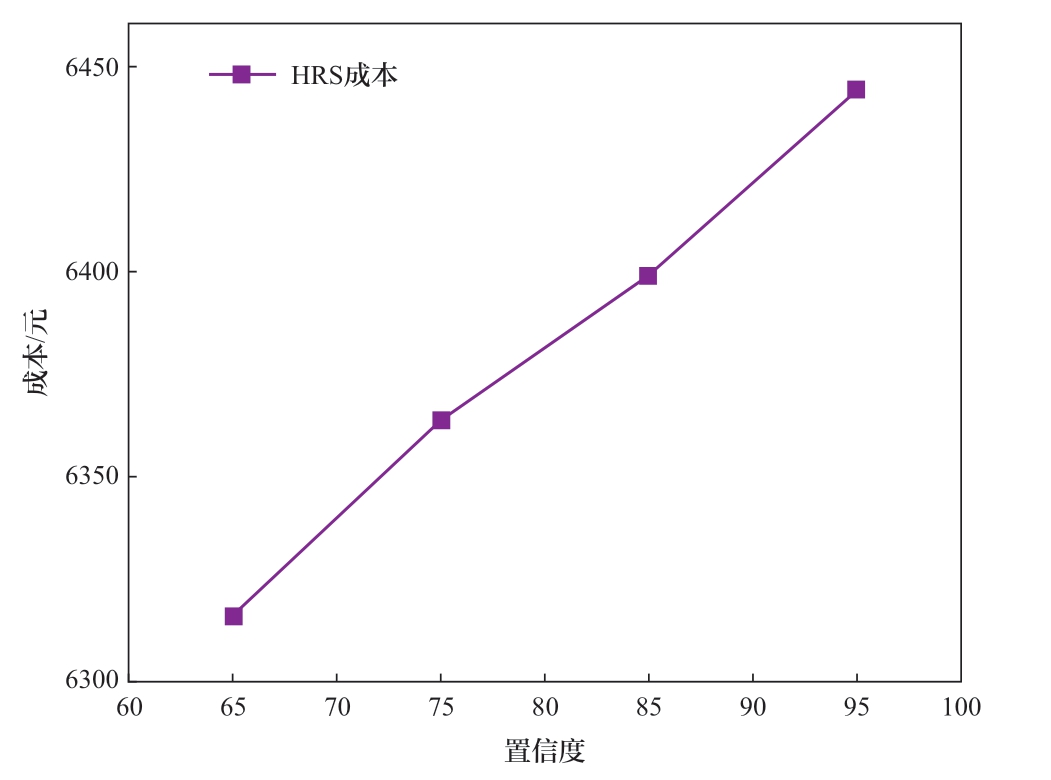
图13 置信度敏感性分析图
Fig. 13 Confidence sensitivity analysis
本文研究中的不确定性相关参数是从整体角度进行分析的,并且这些参数在电源和负荷中的设置都是一致的。在调度策略的实际实施中,IES和HRS可以根据自身情况选择合适的不确定性参数,灵活调整调度策略,实现收益与风险的平衡。
5 结论
本文提出了一种基于Stackelberg博弈理论的加氢站购电鲁棒定价方法,其中IES运营商作为领导者优化电价和调度计划,加氢站作为跟随者优化购电量。模型中嵌入了可再生能源电力、电热负荷、氢负荷等多重不确定性,保证了电价和调度计划的鲁棒性。最后,将该模型转化为两阶段鲁棒优化问题,并采用C&CG算法求解。实例研究验证了该方法的优越性。主要结论如下。
1) 本文所提考虑多重不确定性的定价策略,实现了IES与HRS成本最小化的双赢。此外,本文所提鲁棒博弈定价策略在兼顾风险规避的同时,还低于电网的分时定价,进一步降低了HRS的购能成本,增加了IES的售电收益。
2) 两阶段鲁棒和分布鲁棒机会约束模型考虑了多重不确定性,提高了IES和HRS运营的鲁棒性,系统鲁棒调度方案的运行成本增加,但应对风险的能力增强。方案的保守性取决于不确定参数集的取值。在实践中,系统决策者可以根据自身情况,选择合适的不确定参数,灵活调整运营策略,实现收益与风险的平衡。
3) 本文提出的主从两阶段鲁棒优化模型能够有效地解决源荷多重不确定性带来的风险,实现各主体的经济性与稳健性之间的平衡。此外,本文提供了严格的理论证明,将定价模型转换为可以用现有方法有效求解的经典TSRO模型。
本文的模型中尚未考虑分时电价的不确定性,未来研究将着眼于分析分时电价不确定性对IES优化调度和电价以及HRS购能计划的影响。
参考文献
-
[1]
李剑峰,姜涛,窦文雷,等. 电-热-氢综合能源系统鲁棒区间优化调度[J]. 电力工程技术,2024,43(2): 44-54.LI Jianfeng, JIANG Tao, DOU Wenlei, et al. Robust interval optimal dispatch of integrated electricity and district heating system[J]. Electric Power Engineering Technology, 2024,43(2): 44-54(in Chinese). [百度学术]
-
[2]
REZAEE JORDEHI A, MANSOURI S A, TOSTADO-VÉLIZ M, et al. A tri-level stochastic model for operational planning of microgrids with hydrogen refuelling station-integrated energy hubs[J]. International Journal of Hydrogen Energy,2024, 96: 1131-1145. [百度学术]
-
[3]
GHAITHAN A M. Multi-objective model for designing hydrogen refueling station powered using on-grid photovoltaicwind system[J]. Energy, 2024, 312: 133464. [百度学术]
-
[4]
滕越,赵骞,袁铁江, 等. 绿电-氢能-多域应用耦合网络关键技术现状及展望[J]. 发电技术,2023,44(3):318-330.TENG Yue, ZHAO Qian, YUAN Tiejiang, et al. Key technology status and outlook for green electricity-hydrogen energy-multi-domain applications coupled network[J]. Power Generation Technology, 2023, 44(3): 318-330(in Chinese). [百度学术]
-
[5]
夏佳伟,张一帆,雷浩,等. 考虑高效氢能利用和碳捕集的综合能源系统低碳优化调度[J]. 电力建设,2024,45(12):100-111.XIA Jiawei, ZHANG Yifan, LEI Hao, et al. Low-carbon economic dispatch of integrated energy system considering efficient hydrogen utilization and carbon capture equipment[J].Electric Power Construction, 2024, 45(12): 100-111 (in Chinese). [百度学术]
-
[6]
国家发展改革委,国家能源局. 氢能产业发展中长期规划(2021—2035年)[EB/OL].[2023-06-15].http://zfxxgk.nea.gov.cn/1310525630_16479984022991n.pdf. [百度学术]
-
[7]
CAI P C, MI Y, MA S Y, et al. Hierarchical game for integrated energy system and electricity-hydrogen hybrid charging station under distributionally robust optimization[J].Energy, 2023, 283: 128471. [百度学术]
-
[8]
卞海红,李灿,童宇轩. 共享储能模式下电动汽车充电站双层优化运行策略[J]. 电力工程技术,2024(5):170-180.BIAN Haihong, LI Can, TONG Yuxuan. Optimized operation strategy of electric vehicle charging stations in shared energy storage mode on two layers[J]. Electric Power Engineering Technology, 2024(5): 170-180 (in Chinese). [百度学术]
-
[9]
徐先峰,马文昊,卢勇,等. 基于充电站谐波特性的频率自适应有源电力滤波控制策略[J]. 电力系统保护与控制,2024,52(21):24-34.XU Xianfeng, MA Wenhao, LU Yong, et al. Frequency adaptive active power filtering control strategy based on harmonic characteristics of a charging station[J]. Power System Protection and Control, 2024, 52(21): 24-34(in Chinese). [百度学术]
-
[10]
张家美,孙凯,李洪涛,等. 考虑光-车-氢接入的新型城市配电网规划研究综述与展望[J]. 高电压技术,2024,50(3):1067-1079.ZHANG Jiamei, SUN Kai, LI Hongtao, et al. Review and prospect of future city distribution networks considering the integration of PV-EV-hydrogen[J]. High Voltage Engineering,2024, 50(3): 1067-1079 (in Chinese). [百度学术]
-
[11]
任洲洋,罗潇,覃惠玲,等. 考虑储氢物理特性的含氢区域综合能源系统中长期优化运行[J]. 电网技术,2022,46(9):3324-3332.REN Zhouyang, LUO Xiao, QIN Huiling, et al. Mid/longterm optimal operation of regional integrated energy systems considering hydrogen physical characteristics[J]. Power System Technology, 2022, 46(9): 3324-3332 (in Chinese). [百度学术]
-
[12]
ELMASRY Y, MANSIR I B, ABUBAKAR Z, et al.Electricity-hydrogen nexus integrated with multi-level hydrogen storage, solar PV site, and electric-fuelcell car charging stations[J]. International Journal of Hydrogen Energy,2024, 76: 160-171. [百度学术]
-
[13]
ZGHAIBEH M, BEN BELGACEM I, BARHOUMI E M, et al.Optimization of green hydrogen production in hydroelectricphotovoltaic grid connected power station[J]. International Journal of Hydrogen Energy, 2024, 52: 440-453. [百度学术]
-
[14]
JIANG Y W, HUANG W J, YANG G M. Electrolysis plant size optimization and benefit analysis of a far offshore windhydrogen system based on information gap decision theory and chance constraints programming[J]. International Journal of Hydrogen Energy, 2022, 47(9): 5720-5732. [百度学术]
-
[15]
王艳松,王毓铎. 计及电制氢和碳捕集的园区综合能源系统动态规划[J]. 中国石油大学学报(自然科学版),2024,48(2):142-150.WANG Yansong, WANG Yuduo. Dynamic programming of park-level integrated energy system considering electricity hydrogen production and carbon capture[J]. Journal of China University of Petroleum (Edition of Natural Science), 2024,48(2): 142-150 (in Chinese). [百度学术]
-
[16]
邓杰,姜飞,王文烨,等. 考虑电热柔性负荷与氢能精细化建模的综合能源系统低碳运行[J]. 电网技术,2022,46(5):1692-1704.DENG Jie, JIANG Fei, WANG Wenye, et al. Low-carbon optimized operation of integrated energy system considering electric-heat flexible load and hydrogen energy refined modeling[J]. Power System Technology, 2022, 46(5): 1692-1704(in Chinese). [百度学术]
-
[17]
张智泉,陈晓杰,符杨,等. 含海上风电制氢的综合能源系统分布鲁棒低碳优化运行[J]. 电网技术,2025,49(1):41-51.ZHANG Zhiquan, CHEN Xiaojie, FU Yang, et al.Distributionally robust low-carbon optimal operation for integrated energy system including hydrogen production from offshore wind power[J]. Power System Technology, 2025,49(1): 41-51 (in Chinese). [百度学术]
-
[18]
YANG Y Y, XU X, LUO Y C, et al. Distributionally robust planning method for expressway hydrogen refueling station powered by a wind-PV system[J]. Renewable Energy, 2024,225: 120210. [百度学术]
-
[19]
XU X, HU W H, LIU W, et al. Risk-based scheduling of an offgrid hybrid electricity/hydrogen/gas/refueling station powered by renewable energy[J]. Journal of Cleaner Production, 2021,315: 128155. [百度学术]
-
[20]
LI G G, LI Q Q, YANG X, et al. General Nash bargaining based direct P2P energy trading among prosumers under multiple uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2022, 143: 108403. [百度学术]
-
[21]
XIE W J, AHMED S. Distributionally robust chance constrained optimal power flow with renewables: a conic reformulation[J]. IEEE Transactions on Power Systems, 2017,33(2): 1860-1867. [百度学术]
-
[22]
GUO J X, YANG J, ZHAO Y Z, et al. Investigations on temperature variation within a type III cylinder during the hydrogen gas cycling test[J]. International Journal of Hydrogen Energy, 2014, 39(25): 13926-13934. [百度学术]
-
[23]
GABRIEL S A, CONEJO A J, FULLER J D, et al.Complementarity modeling in energy markets[M]. Cham:Springer New York, 2013. [百度学术]
-
[24]
NOCEDAL J, WRIGHT S J. Numerical optimization[M].Cham: Springer New York, 2006. [百度学术]
-
[25]
朱少闻. 考虑需求侧管理的综合能源系统均衡交互策略研究[D]. 北京:华北电力大学,2020. [百度学术]
-
[26]
Gurobi Optimization, Inc. Modeling 2 [EB/OL]. (2016-01-01)[2025-02-25]. https://assets.gurobi.com/pdfs/user-events/2017-frankfurt/Modeling-2.pdf. [百度学术]
-
[27]
BOYD S P, VANDENBERGHE L. Convex optimization[M].Cambridge university press, 2004. [百度学术]
-
[28]
BERTSEKAS D, NEDIC A, OZDAGLAR A. Convex analysis and optimization[M]. Athena Scientific, 2003. [百度学术]
-
[29]
ZENG B, ZHAO L. Solving two-stage robust optimization problems using a column-and-constraint generation method[J].Operations Research Letters, 2013, 41(5): 457-461. [百度学术]
-
[30]
ZHAI J Y, ZHOU M, LI J N, et al. Hierarchical and robust scheduling approach for VSC-MTDC meshed AC/DC grid with high share of wind power[J]. IEEE Transactions on Power Systems, 2021, 36(1): 793-805. [百度学术]
-
[31]
LU S, GU W, XU Y J, et al. Unlock the thermal flexibility in integrated energy systems: a robust nodal pricing approach for thermal loads[J]. IEEE Transactions on Smart Grid, 2023,14(4): 2734-2746. [百度学术]
-
[32]
QIU H F, GOOI H B, GAO H J, et al. Cooperative power bidding of smart community grids with an aggregatorprosumer-based hierarchical framework[J]. IEEE Transactions on Smart Grid, 2023, 14(4): 3032-3045. [百度学术]
-
[33]
丁涛,贾文皓,黄雨涵,等. 基于分布鲁棒机会约束的移动氢能系统制-储-运氢协同优化[J]. 电力系统自动化,2023,47(23):1-11.DING Tao, JIA Wenhao, HUANG Yuhan, et al. Collaborative optimization for hydrogen generation, storage, and transportation in mobile hydrogen energy systems based on distributionally robust chance constraint[J]. Automation of Electric Power Systems, 2023, 47(23): 1-11 (in Chinese). [百度学术]
基金项目
国家自然科学基金资助项目(72273042)。
National Natural Science Foundation of China (72273042).


