相关论文:
-

-
全球能源互联网
第8卷 第5期 2025年09月;页码:615-624
提升风电接入系统可用输电能力的混合型潮流控制器双层优化配置
Bi-level Optimal Configuration of Hybrid Power Flow Controller for Enhancing Available Transfer Capability of Wind Power Integrated System
- 1.国网江苏省电力有限公司经济技术研究院,江苏省 南京市 210008
- 2.东南大学电气工程学院,江苏省 南京市 210096
- CAI Hui1, QI Wanchun1, HAN Xingning1, GUAN Chenhao2, SUN Wentao1, WU Xi2* (1. Economic Research Institute, State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210008, Jiangsu Province, China
- 2. School of Electrical Engineering, Southeast University, Nanjing 210096, Jiangsu Province, China
关键词
Keywords
摘 要
Abstract
为了解决大规模风电接入所导致的可用输电能力(available transfer capability,ATC)受限问题,提出了一种提升风电接入系统ATC的混合型潮流控制器(hybrid power flow controller,HPFC)选址定容方法。首先,基于功率注入法建立HPFC的数学模型,并采用改进K均值(K-means)聚类算法削减风电、负荷概率场景;其次,建立了计及ATC的HPFC双层优化配置模型,上层优化模型以最小化HPFC配置成本和节点电压偏移为目标,下层以最大化系统ATC为目标;最后,应用改进多目标粒子群(multi-objective particle swarm optimization,MOPSO)算法计算所提双层优化模型的Pareto解集,根据解集中每个解的模糊满意度函数确定最优解。
To effectively address the limited available transfer capability (ATC) issue caused by large-scale wind power integration, a hybrid power flow controller (HPFC) siting and sizing method for enhancing the available transfer capability(ATC) of wind integration power systems is proposed.Firstly, the mathematical model of HPFC is established based on the power injection method, and an improved K-means clustering algorithm is employed to reduce wind power and load probability scenarios. Secondly, a bi-level optimization configuration model for HPFC considering ATC is developed.The upper level aims to minimize the HPFC configuration cost and bus voltage deviation, while the lower level aims to maximize the system’s ATC. Finally, the improved multiobjective particle swarm optimization (MOPSO) algorithm is applied to compute the Pareto solution set of the proposed bilevel optimization model, and the optimal solution is determined based on the fuzzy satisfaction function of each solution in the solution set.
0 引言
2020年9月中国明确提出“双碳”目标[1]。为实现“双碳”目标,大规模区外水、风、光等新能源将持续接入电网,电力系统作为能源枢纽将发挥重要作用,构建以新能源为主的新型电力系统迫在眉睫[2]。然而,新能源本身具有很强随机性与时序性,这会对电网的潮流分布产生巨大影响,引发线路过载、可用输电能力(available transfer capability,ATC)受限等问题,对规模化新能源消纳和电网的供电能力提升产生影响,给电网运行带来较大的安全隐患[3]。
传统的确定性ATC计算方法主要包括灵敏度法、重复潮流法、连续潮流法和最优潮流法[4-5]。文献[6]提出了一种具有步长控制机制的改进重复交流潮流计算方法,用于分析电力系统在双向输电过程中的ATC。文献[7]以负荷节点有功功率增量之和为目标函数,以系统的静态安全性和稳定性为约束条件,构建了ATC的优化模型。文献[8]提出了一种基于线性化最优潮流的ATC计算方法,并通过实验验证了该方法优于基于直流潮流和交流潮流的ATC算法。然而,确定性ATC计算方法并未考虑到新能源等不确定因素对系统潮流的影响,无法有效适应大量新能源接入背景下系统ATC的计算[9]。针对确定性ATC计算方法的局限性,有研究提出了概率性ATC计算方法,并被广泛地应用于考虑新能源等不确定因素的电力系统ATC计算。文献[10]提出了一种基于区间优化的ATC评估模型,从而在考虑风电不确定性的情况下确定可能的ATC范围。文献[11]利用最优性条件分解技术和拉丁超立方体抽样方法来实现风能资源渗透电力系统的ATC概率评估。文献[12]基于多项式混沌展开实现概率ATC到确定ATC的转化。
近年来,统一潮流控制器(unified power flow controller,UPFC)已在中国多地得到应用,其通过对网络参数快速、准确、灵活的调整,从而调控输电线路中的潮流,成为提升系统输电能力和稀缺廊道资源的输电效率的有效途径之一[13]。然而,由于UPFC为了满足高压大容量的需要,装置的成本很高,极大地限制了UPFC的推广[14]。有研究提出了兼顾经济性和功能性的混合型潮流控制器(hybrid power flow controller,HPFC)。在HPFC中,“Sen”变压器(“Sen”transformer,ST)负责大容量的潮流调节,UPFC负责小容量的精确控制,装置内部的电磁元件的容量要大于电力电子元件的容量,从而有效降低了装置成本[15]。同时,HPFC中的UPFC能在ST粗调节的基础上进行精确补偿,且能在潮流调节需求较小时单独进行潮流调节,减少了ST的操作次数,响应速度也比传统ST更快[16]。在保证控制能力的同时大幅降低成本,为提升系统ATC提供了新的技术方案。
在利用FACTS设备增强ATC方面,国内外都进行了广泛的研究。文献[17]提出了一种基于多种FACTS协调规划的ATC增强方法,并结合混合实际潮流性能指数与粒子群优化实现FACTS规划方案的求解。文献[18]将脑风暴优化算法应用于FACTS设备的优化配置,从而有效提升电力系统的ATC。文献[19-20]以提高系统ATC为目标,通过交流功率传输分配因子确定TCSC在电网中的最佳配置位置。文献[21]研究了两阶段FACTS设备优化配置方法,先基于灵敏度优化FACTS设备的位置,再分别采用元启发式进化粒子群优化计算ATC。文献[22]考虑了多风电场不确定性和相关性,使用非支配排序遗传算法和内点法确定最优SSSC配置方案,同时显著提高了系统ATC。
尽管现有的概率性方法在计算高比例新能源电力系统的ATC方面比确定性方法具有更好的性能,但大多数概率性方法的计算成本都很高[23]。此外,现有研究在利用FACTS设备提升系统ATC方面大多并未计及新能源输出不确定性,所用优化配置方法无法适应未来电网的发展趋势。针对以上问题,本文提出一种提升风电接入系统ATC的HPFC双层优化配置方法,充分计及风电、负荷波动对电网潮流的影响,在确保电网安全运行的同时利用最少的HPFC配置成本最大限度提升系统ATC,得到HPFC的最优配置方案。首先,基于功率注入法给出了一种适用于双回线控制的HPFC稳态数学模型。其次,采用改进K均值(K-means)聚类算法建立能表征风电、负荷不确定性的概率场景。接着,建立HPFC双层优化配置模型,实现HPFC配置成本、节点电压偏移和系统ATC的分层求解,并通过改进多目标粒子群(multi-objective particle swarm optimization,MOPSO)算法求解所提高度非线性优化问题。
1 HPFC的数学模型及经济性分析
1.1 HPFC数学模型
考虑到现有220 kV及以上电网中的线路大多采用双回线结构,为了扩展HPFC的应用场景,提出一种适用于双回线控制的HPFC。该HPFC在双回线UPFC结构的基础上加入两个ST,UPFC经双回线对应的两条控制线路并入电网,每条控制线路对应串联一个ST,具体结构如图1所示。
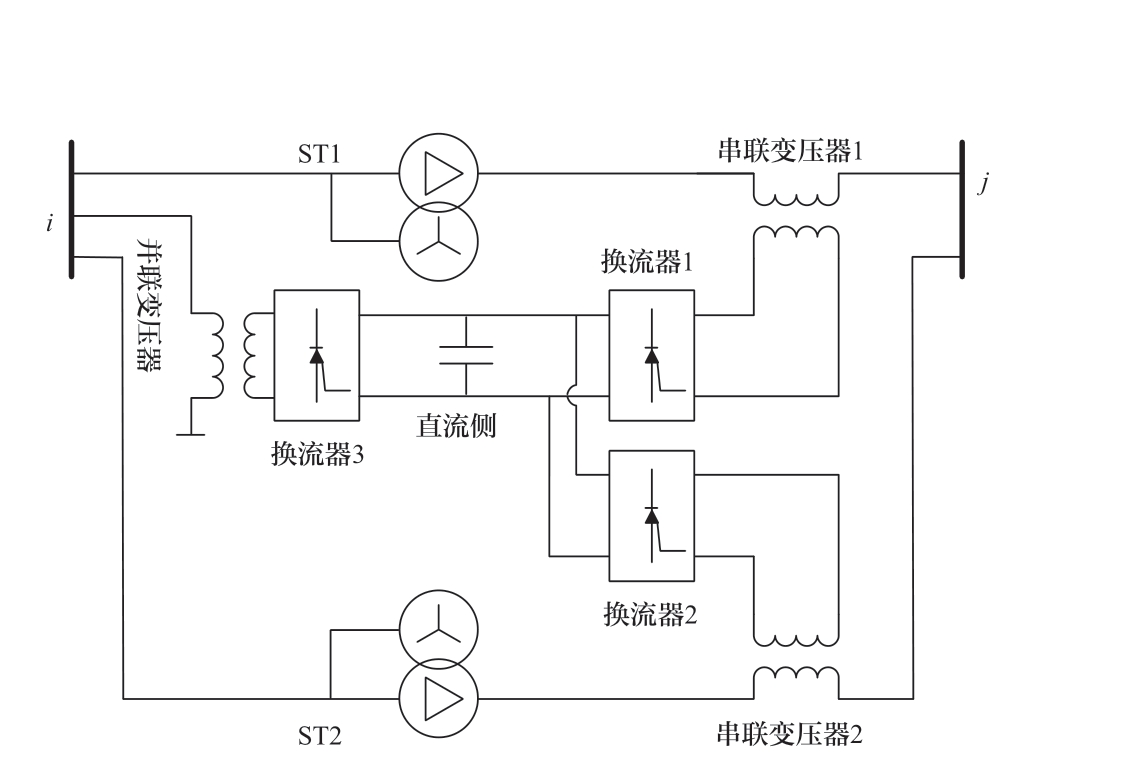
图1 HPFC的基本结构
Fig. 1 Basic structure of HPFC
依据FACTS设备的常规等效方法,得到HPFC等效电路图如图2所示。
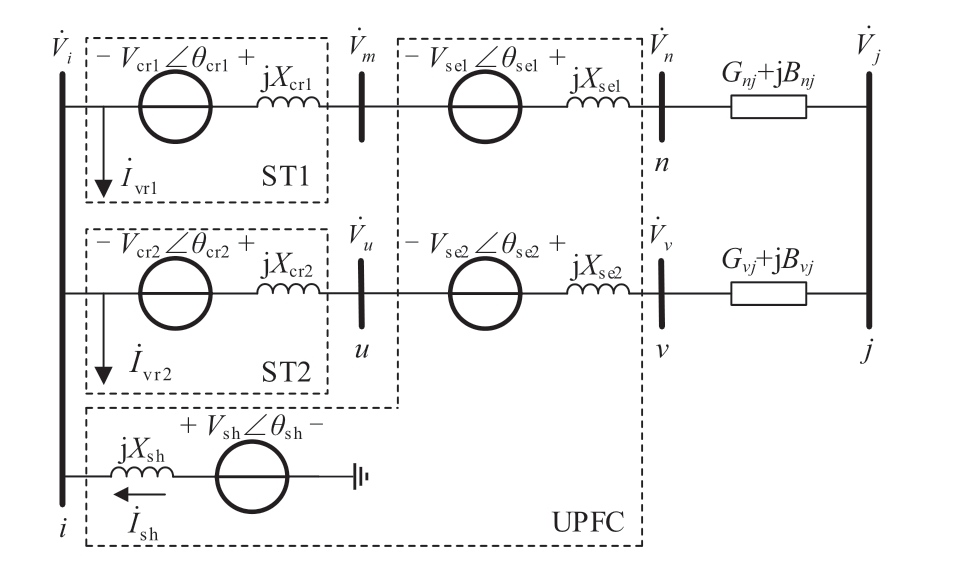
图2 HPFC的等效电路图
Fig. 2 Equivalent circuit diagram of HPFC
图2中,双回线ij为HPFC接入线路,m、n、u、v为方便后续公式推导而添加的附加节点,HPFC实际控制线路为线路nj和线路vj;![]()
![]() 分别为对应节点的电压相量;Vcr1、Vcr2、θcr1、θcr2分别为ST1和ST2的电压调节单元电压幅值及相角;Vse1、Vse2、θse1、θse2分别为UPFC接入对应单回线的串联侧换流器电压幅值及相角;
分别为对应节点的电压相量;Vcr1、Vcr2、θcr1、θcr2分别为ST1和ST2的电压调节单元电压幅值及相角;Vse1、Vse2、θse1、θse2分别为UPFC接入对应单回线的串联侧换流器电压幅值及相角;![]() 分别为ST1和ST2的并联侧注入电流相量;Vsh、θsh分别为UPFC并联侧换流器的电压幅值和相角;
分别为ST1和ST2的并联侧注入电流相量;Vsh、θsh分别为UPFC并联侧换流器的电压幅值和相角;![]() 为流经UPFC并联侧换流器的电流相量;Xcr1、Xcr2分别为ST1和ST2的串联耦合变压器等效电抗;Xse1、Xse2分别为UPFC接入对应单回线的串联耦合变压器等效电抗;Xsh为UPFC的并联耦合变压器等效电抗;Gnj、Bnj、Gvj、Bvj分别为线路nj和线路vj的等效电导、电纳。
为流经UPFC并联侧换流器的电流相量;Xcr1、Xcr2分别为ST1和ST2的串联耦合变压器等效电抗;Xse1、Xse2分别为UPFC接入对应单回线的串联耦合变压器等效电抗;Xsh为UPFC的并联耦合变压器等效电抗;Gnj、Bnj、Gvj、Bvj分别为线路nj和线路vj的等效电导、电纳。
依据功率注入法将各电压源对线路的影响转化为对节点的注入功率,可以得到
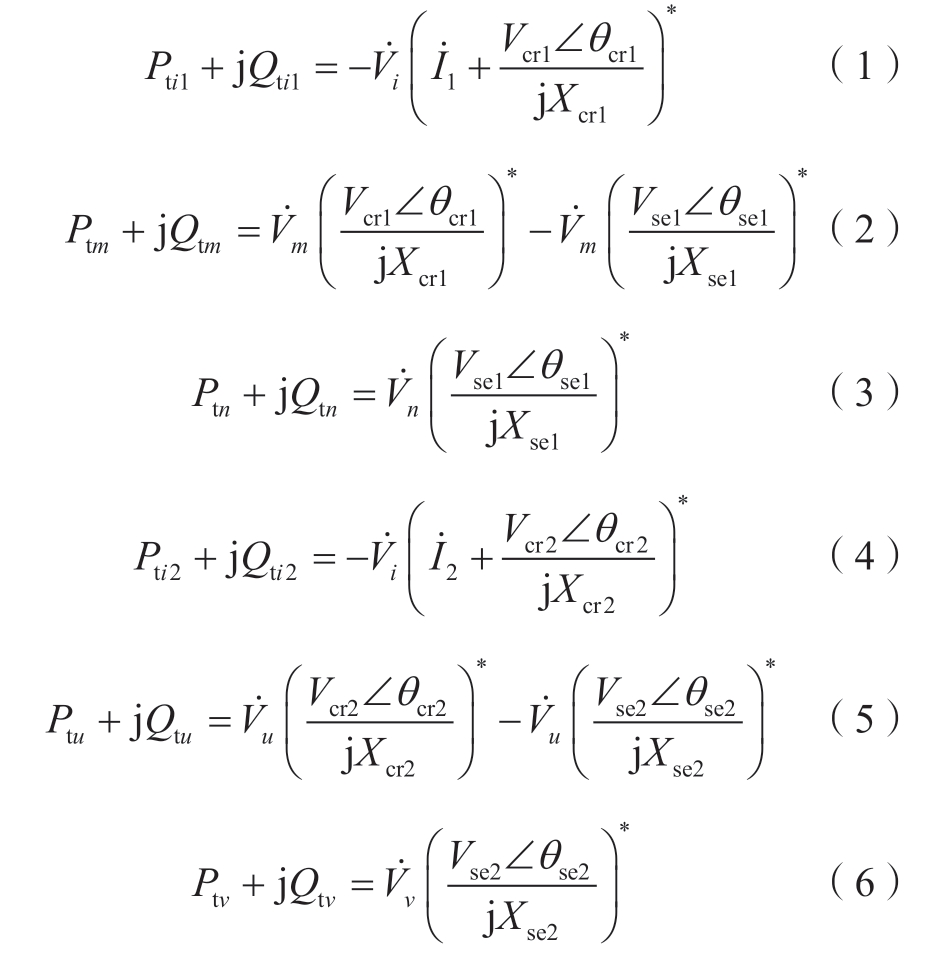
式中:Pt i1 、Pt i2分别为HPFC串联侧对节点i的有功注入功率的第一和第二分量;Qt i1、Qt i2分别为HPFC串联侧对节点i的无功注入功率的第一和第二分量;Ptm、Ptn、Ptu、Ptv分别为HPFC对节点m、n、u、v的有功注入功率;Qtm、Qtn、Qtu、Qtv分别为HPFC对节点m、n、u、v的无功注入功率。
依据HPFC内部换流器的有功守恒,可得
式中:Psh为HPFC并联侧对节点i的有功注入功率。
通过式(1)—(7)可以将HPFC对于线路的影响转化为节点注入功率,进而能利用牛顿-拉夫逊法求解含HPFC系统的潮流。
1.2 HPFC的经济性分析
HPFC的总成本由两部分组成,一部分来自ST的大容量,另一部分来自UPFC的小容量,UPFC和ST的容量比会极大地影响HPFC的总成本。对于HPFC的串联侧而言,流经UPFC和ST的电流大致相等,故UPFC和ST的容量比可近似等于UPFC串联侧换流器与ST电压调节单元的电压幅值的比值。当ST抽头数量为1时,以双回线ij中ST1所在的一回线为例,该回线上HPFC的串联侧补偿电压控制范围如图3所示。
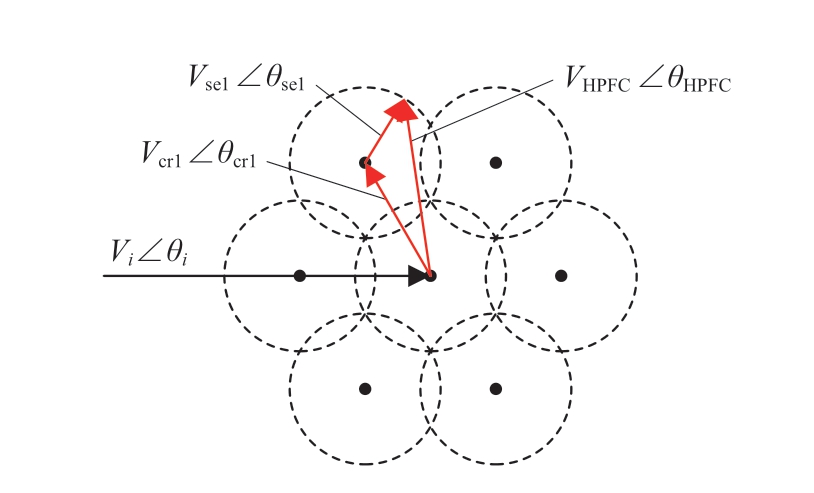
图3 HPFC的串联侧补偿电压控制范围
Fig. 3 Series side compensation voltage control range of HPFC
图3中,VHPFC、θHPFC分别为HPFC的串联侧补偿电压幅值和相角。
图3中的各点表示ST1的电压调节单元可以设置的电压相量,小圆表示UPFC的串联侧换流器电压控制范围,所有小圆组成的控制范围即为HPFC的串联侧补偿电压控制范围。在HPFC中,不仅要满足控制范围内没有控制盲区,还要最大限度减少UPFC的容量,故UPFC与ST的容量以及UPFC串联侧换流器与ST电压调节单元的电压幅值存在一定的比例关系,即
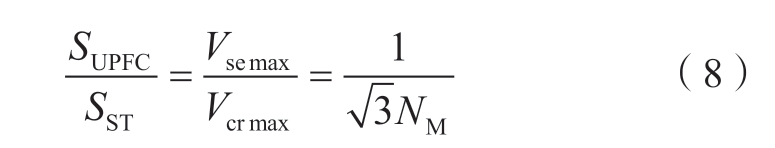
式中:SUPFC和SST分别为UPFC和ST的容量;Vse max为UPFC串联侧换流器电压幅值最大值;Vcr max为ST电压调节单元电压幅值最大值;NM为ST的抽头数量。
进一步分析UPFC和ST的容量比对HPFC的总成本的影响。取ST的制造成本约15万元/MVA,UPFC的制造成本约75万元/MVA[24]。当NM=2时,在HPFC中UPFC和ST的容量比为28.9%,HPFC的成本约为28.44万元/MVA,UPFC的成本约为HPFC的2.6倍。当NM=3时,HPFC中UPFC和ST的容量比为19.2%,HPFC的成本约为24.68万元/MVA,UPFC的成本约为HPFC的3倍。
由此可见,HPFC相比UPFC,其成本大幅减少,且HPFC中ST抽头数量的增加能进一步降低其成本。
2 HPFC双层优化配置模型
为了应用HPFC解决大规模风电接入所导致的电力系统ATC受限问题,本文构建一种提升风电接入系统ATC的HPFC双层优化配置模型,上层优化模型以最小化HPFC配置成本和节点电压偏移为目标,下层优化模型以最大化系统ATC为目标。HPFC双层优化配置中,以基态和极限状态下的机组出力和负荷作为上下层优化模型间的交互信息。上层优化模型基于计及风电不确定性的HPFC优化配置方法,确定HPFC控制变量及基态下的发电机组出力和负荷并传递给下层,辅助下层优化模型计算ATC,下层优化模型则将极限状态下的发电机组出力和负荷传递给上层,对上层优化模型的HPFC规划产生影响。
2.1 上层优化模型
2.1.1 目标函数
上层优化模型重点考虑HPFC的经济性和控制效果,以HPFC配置成本为经济指标,节点电压偏移为效益指标,各目标函数的具体表达式如下。
1)HPFC配置成本。
大功率FACTS装置的配置费用较高,若其装置布点的选择不当、容量配置的方案不佳,则可能造成较大的经济损失。因此,降低配置成本是对FACTS装置进行规划时的重要目标之一。HPFC的配置成本计算式为
式中:f1为HPFC配置成本函数;aH为HPFC的单位容量价格;SH为HPFC换流器稳态运行容量,在考虑多场景的情况下,SH选择的是所有场景所有工况下的最大值。
2)节点电压偏移。
节点电压偏移主要用来衡量节点电压运行点与其参考运行点偏移程度,是保证系统安全运行的重要考虑因素之一。系统的节点电压偏移计算式为
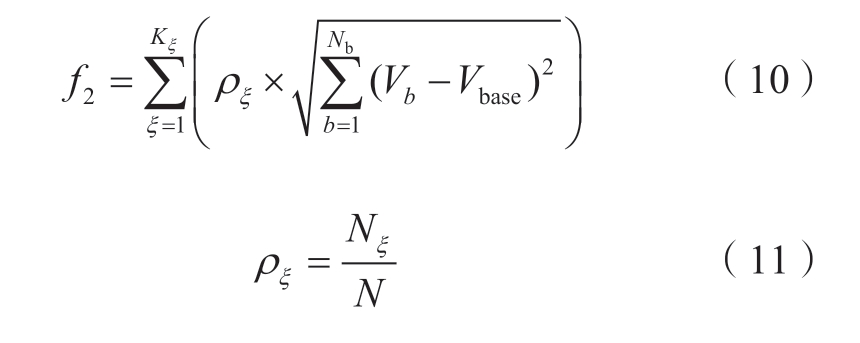
式中:f2为计及多场景的综合节点电压偏移函数;Kξ表示场景个数;ρξ表示第ξ个场景的概率;Nξ表示第ξ个场景中的样本数;Vb为节点b的电压幅值;Nb为系统节点总数;Vbase为节点基准电压。
2.1.2 约束条件
1)等式约束。
电力系统的等式约束主要为节点功率平衡约束,而对于HPFC并联侧节点和附加节点还需要额外计及HPFC的注入功率。此时的节点功率平衡约束可以表示为
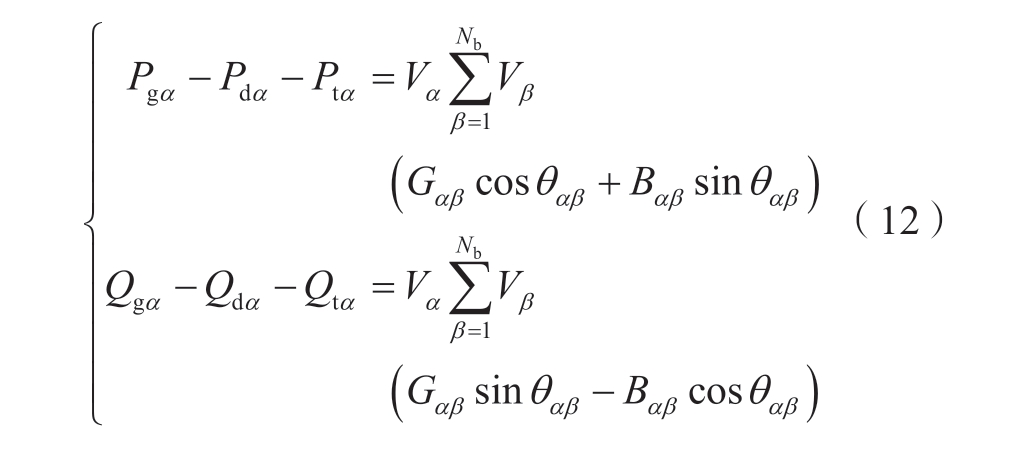
式中:Pgα、Qgα分别为节点α处发电机的有功和无功出力;Pdα、Qdα分别为节点α处的有功和无功负荷;Vα、Vβ分别为节点α和β的电压幅值;Gαβ、Bαβ分别为线路αβ的电导和电纳;θαβ为节点α和β的电压相角差;若节点α为HPFC的接入节点(即α=i, m, n, u, v),则Ptα和Qtα分别为HPFC对该节点的有功、无功注入功率,若α为系统中其他节点,Ptα=Qtα=0。
2)不等式约束。
对于控制变量,有
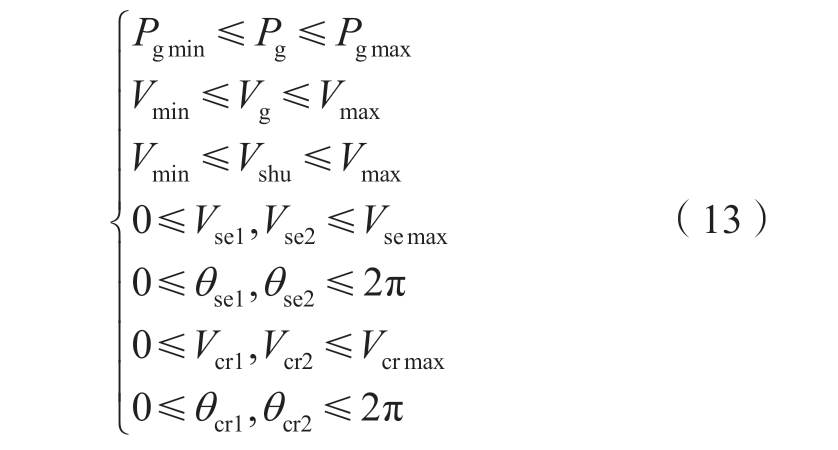
式中:Pg为发电机有功出力;Pg max、Pg min为发电机有功出力上下限;Vg为发电机所接节点电压幅值;Vmax、Vmin为节点电压幅值上下限;Vshu为HPFC并联节点定电压值;Vse max为HPFC中UPFC的换流器电压幅值上限;Vcr max为HPFC中ST的换流器电压幅值上限。
对于状态变量,有
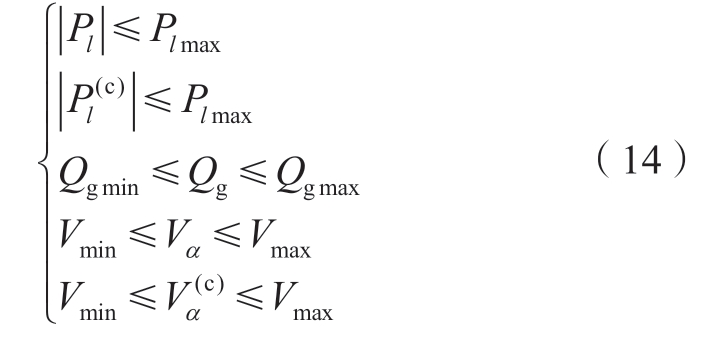
式中:Pl表示线路l上的潮流;Pl max表示线路l的潮流安全极限;(·)(c)表示N-1故障下的状态变量参数值;Qg为发电机无功出力;Qg max、Qg min为发电机无功出力上下限;Pb表示节点α的电压幅值。
2.2 下层优化模型
2.2.1 目标函数
ATC是衡量电力系统在区域之间输电能力的一个重要参数,是反映电网灵活性的指标之一,对于维护系统安全稳定运行具有重要意义。系统ATC可以表示为
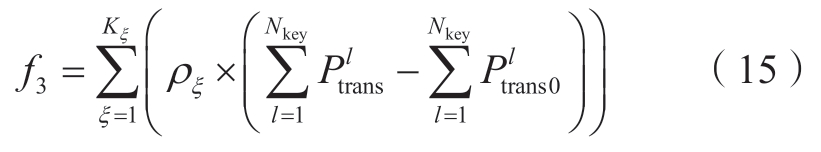
式中:f3为计及多场景的综合系统ATC函数;Nkey为ATC计算断面所包含的线路总数;![]() 为发电机出力和负荷增加后系统达到临界条件时断面线路l的输电能力;
为发电机出力和负荷增加后系统达到临界条件时断面线路l的输电能力;![]() 为断面线路l的原始输电能力。
为断面线路l的原始输电能力。
2.2.2 约束条件
1)等式约束。
下层优化模型需满足临界条件时的节点功率平衡约束为
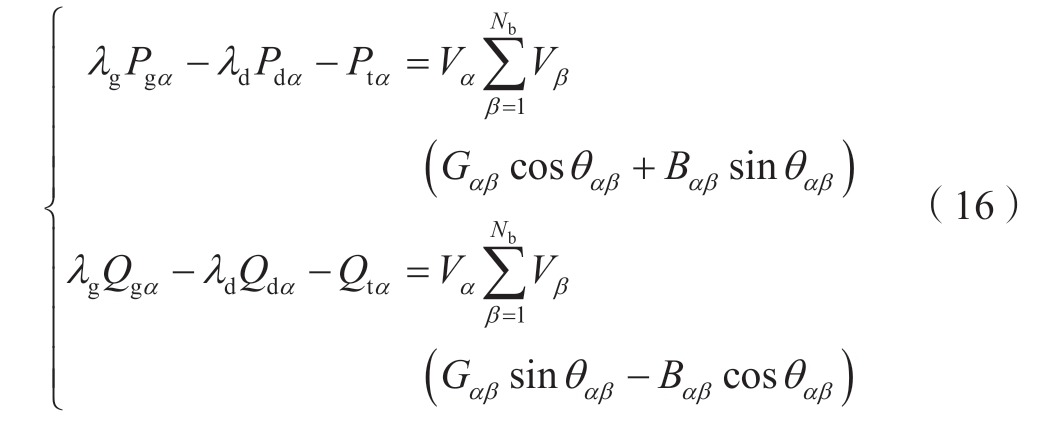
式中:λg为发电机出力增长系数;λd为负荷增长系数。若节点α为发电区节点,则λd=0;若节点α为受电区节点,则λg=0。
2)不等式约束。
对于控制变量和状态变量,有:
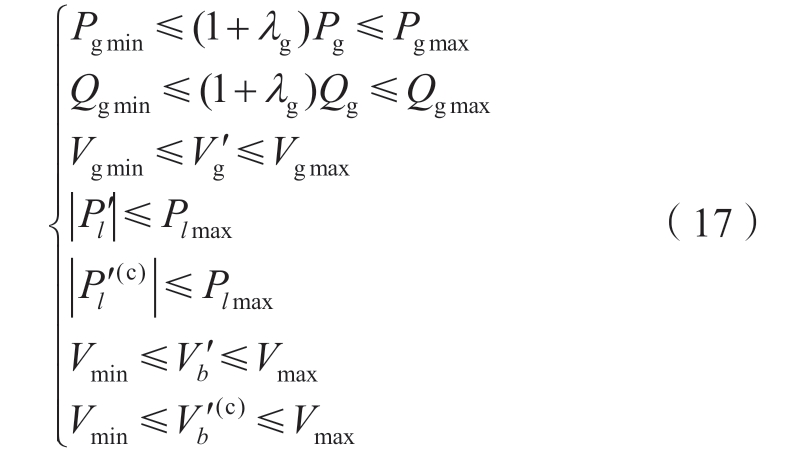
式中:(·)′表示在临界条件下的状态变量参数值。
3 HPFC双层优化配置求解方法与流程
3.1 改进K-means聚类算法
为了解决概率性ATC计算成本高的问题,本文将采用聚类算法对大量风电、负荷数据进行削减,实现计算效率的高效化。K-means聚类是目前常用的聚类算法之一。然而,基于聚类中心选择的随机性,该聚类方法容易得到局部最优解,聚类效果较差。因此,本文采用一种改进K-means聚类算法[25],以获取更加有效的聚类结果。
该方法的具体步骤如下。
①建立样本数据矩阵;
②将欧氏距离最远的2个样本设置为初始聚类中心集合,计算剩余样本与初始聚类中心的欧氏距离,将欧氏距离最远的样本加入初始聚类中心集合,直到有K个样本加入初始聚类中心集合为止;
③依据式(18)计算各样本与不同聚类中心之间的相似性,根据相似性大小将样本分配到不同的聚类
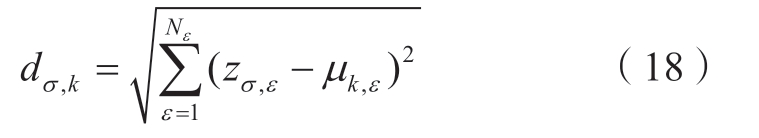
式中:dσ, k为第σ个样本与第k个聚类中心的相似性;Nε为样本维度;zσ,ε为第σ个样本第ε维的值;μk,ε为第k个聚类中心第ε维的值;
④更新各聚类的聚类中心;
⑤重复步骤③和④直至迭代收敛;
⑥依据式(19)和式(20)计算各K值对应的簇内误差平方和(sum of squared error,SSE)指标与CHI(calinski harabasz index)指标,综合考虑两种指标的计算结果选取最佳的聚类集合。
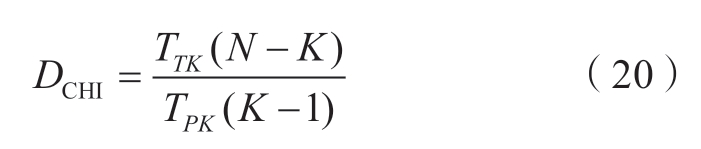
式中:K为聚类数目;Nk为聚类k中的样本数目;yk, γ, ε为聚类k中第γ个样本第ε维的值;TTK为类间离差平方和;N为样本总数。
3.2 改进MOPSO算法
由于所建立的HPFC优化配置模型呈现很强的非线性,故本文采用改进MOPSO算法实现模型的求解。
传统MOPSO算法的初始粒子通常是随机生成的,这容易导致初始粒子分布不均匀,从而对算法的收敛性造成不利影响,最终会陷入局部最优的情况。而采用混沌初始化粒子可以有效避免初始粒子分布不均匀的问题,因此本文基于Tent混沌映射初始化粒子[26],其计算式为
式中:η表示粒子序号。
混沌初始化的步骤为:随机生成取值范围在0~1的混沌变量x0,把x0代入式(21)进行多次迭代,将迭代后的混沌变量映射至粒子位置的取值范围,生成初始粒子群。
为了更近一步提升MOPSO算法的寻优速度和寻优能力,将原本MOPSO算法的惯性权重从固定权重更改为变权重,使得惯性权重可以随着迭代次数的变化而变化。改进后的MOPSO算法的粒子速度和位置更新公式如式(22)所示。
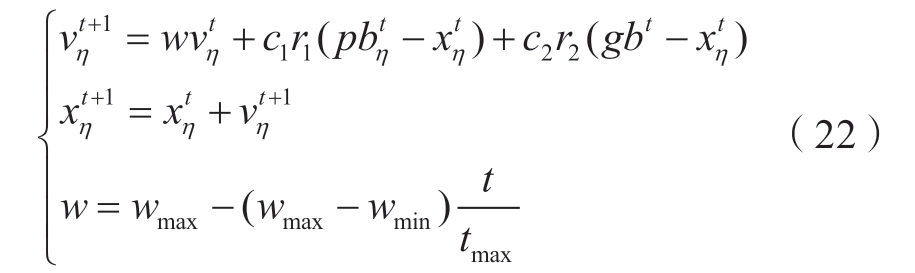
式中:![]() 分别表示第η个粒子第t次迭代的位置和速度;tmax为最大选代次数;c1、c2为加速度因子,均取为2;r1、r2分别表示0~1内的随机数;
分别表示第η个粒子第t次迭代的位置和速度;tmax为最大选代次数;c1、c2为加速度因子,均取为2;r1、r2分别表示0~1内的随机数;![]() 表示第η个粒子在历史搜索中的最优位置;gbt表示第t次选代变量的群体最优位置;w、wmax和wmin分别为惯性权重及其上下限值。
表示第η个粒子在历史搜索中的最优位置;gbt表示第t次选代变量的群体最优位置;w、wmax和wmin分别为惯性权重及其上下限值。
根据式(23)计算各Pareto解的模糊满意度,模糊满意度最大的即为最优解。
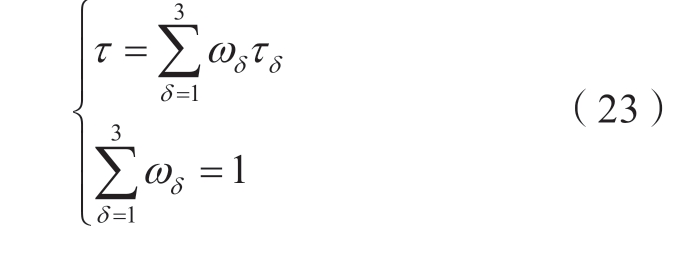
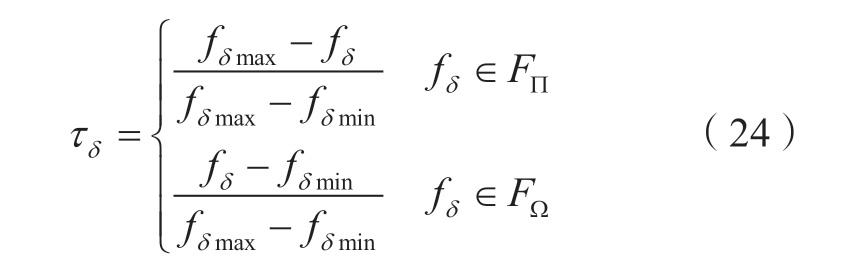
式中:τδ表示该Pareto解的第δ个目标函数的模糊满意度值;ωδ表示第δ个目标函数的权重;fδ为该Pareto解的第δ个目标函数;fδ max、fδ min分别为Pareto解集中第δ个目标函数的最大、最小值;FΠ、FΩ分别表示成本型函数和效益型函数。
在本文中,为了平等地考虑HPFC配置成本、节点电压偏移、ATC等3个指标,设置权重ω1=ω2=ω3=1/3。考虑到在实际工程中,不同的指标可能会由于现实情况的不同而有所侧重,此时也可根据相关领域专家的经验或者采用熵权法等权重分析方法来重新对权重赋值。
3.3 HPFC优化配置方法流程
本文所提出的提升风电接入系统ATC的HPFC双层优化配置模型求解流程如图4所示。首先,采用改进K-means聚类算法生成风电–负荷概率场景。其次,在不同的场景下进行HPFC优化配置计算。在HPFC优化配置的每次迭代过程中,上下层模型之间通过基态和极限状态下的发电机组出力和负荷来进行交互。上层优化模型采用改进MOPSO算法确定HPFC控制变量及基态下的发电机组出力和负荷,辅助下层优化模型计算ATC;下层优化模型在利用内点法求解ATC的同时获取极限状态下的发电机组出力和负荷,并传递给上层优化模型用于计算HPFC的容量。
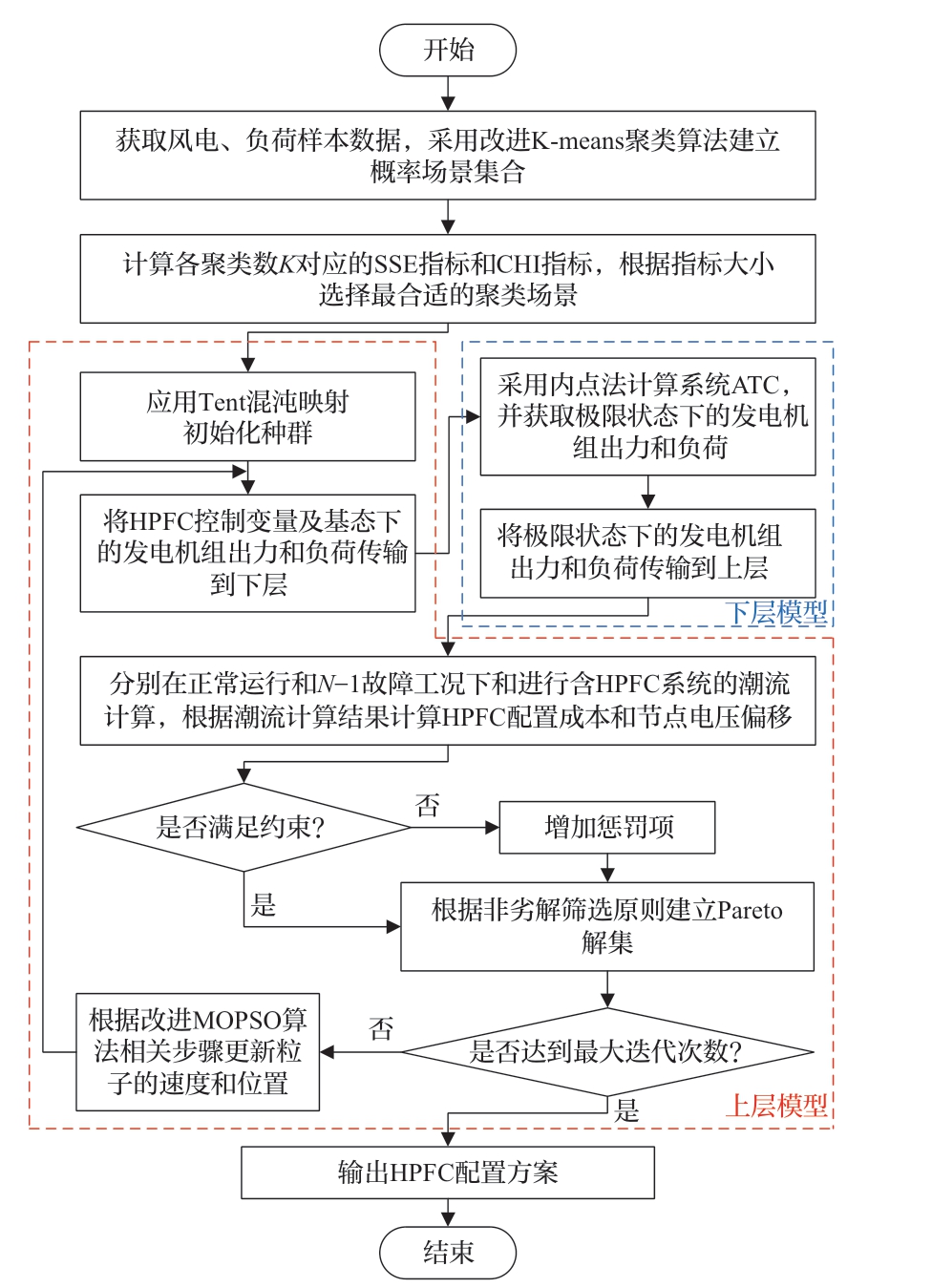
图4 HPFC双层优化配置方法流程图
Fig. 4 Flow chart of bi-level optimization configuration method for HPFC
4 算例分析
本文选择2025年江苏电网500 kV规划网架为研究对象,重点关注利用HPFC提升江苏电网过江断面(包括秋藤–秦淮线路、三汊湾–龙王山线路、江都–大港线路、泰兴–斗山线路、凤城–梅里线路共5条500 kV双回线)的输电能力,提出HPFC的最佳配置方案,并对比分析了本文所提方法与单层优化配置方法的效果,还进一步分析了本文所提方法计算结果的稳定性。
4.1 风电/负荷场景计算
本文采用江苏电网2019年的风电出力系数和系统总负荷数据(采样间隔为5 min)作为改进K-means聚类分析的样本数据,分别获取聚类数K=2~15时对应的风电出力系数和系统总负荷聚类集合,并计算不同聚类数对应的SSE指标和CHI指标结果如图5所示。
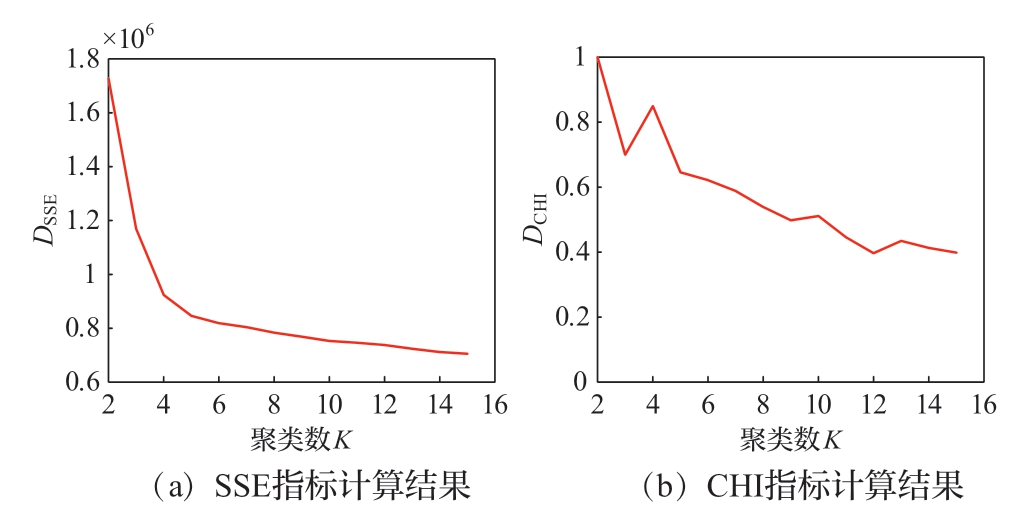
图5 不同聚类数对应的SSE指标和CHI指标计算结果
Fig. 5 Calculation results of SSE and CHI corresponding to different cluster numbers
从图5可以看出,SSE曲线的拐点位于聚类数为3~6的范围内,而聚类数为2或4时对应的CHI指标值相对较大。综合两种指标的分析结果,聚类数为4时的聚类效果最好,最终得到的4个聚类场景相关数据如表1所示。
表1 各场景的风电/负荷数据及场景概率
Table 1 Wind power/load data and scenario probabilities for each scenario
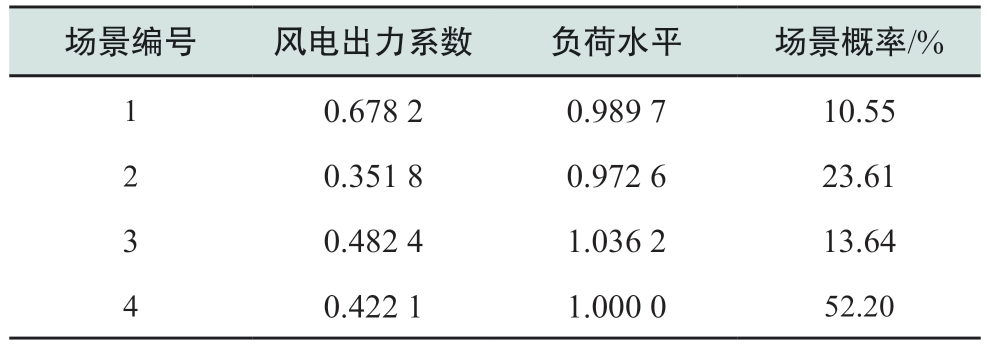
场景编号 风电出力系数 负荷水平 场景概率/%1 0.678 2 0.989 7 10.55 2 0.351 8 0.972 6 23.61 3 0.482 4 1.036 2 13.64 4 0.422 1 1.000 0 52.20
4.2 HPFC优化配置结果
改进MOPSO算法的参数设置如下所示:粒子数为50个;最大迭代次数为200次;惯性权重上下限为0.9和0.4。HPFC的相关参数设置如下:ST的输出电压幅值上限为0.5 pu,抽头数量为4;UPFC的输出电压幅值上限为0.072 2 pu;HPFC的单位容量成本为22.567 9万元/MVA。此外,系统的容量基准值设置为100 MVA。考虑到本研究的目的为利用HPFC提升江苏电网过江断面的输电能力,故将HPFC的选址位置初步设定为5条过江断面,采用所提优化配置方法计算在不同选址方案下的综合最优容量配置对应目标函数计算结果如表2所示。
表2 不同选址方案下的HPFC最优容量配置对应综合目标函数计算结果
Table 2 Calculation results of the comprehensive objective function corresponding to the optimal capacity allocation of HPFC under different site selection schemes
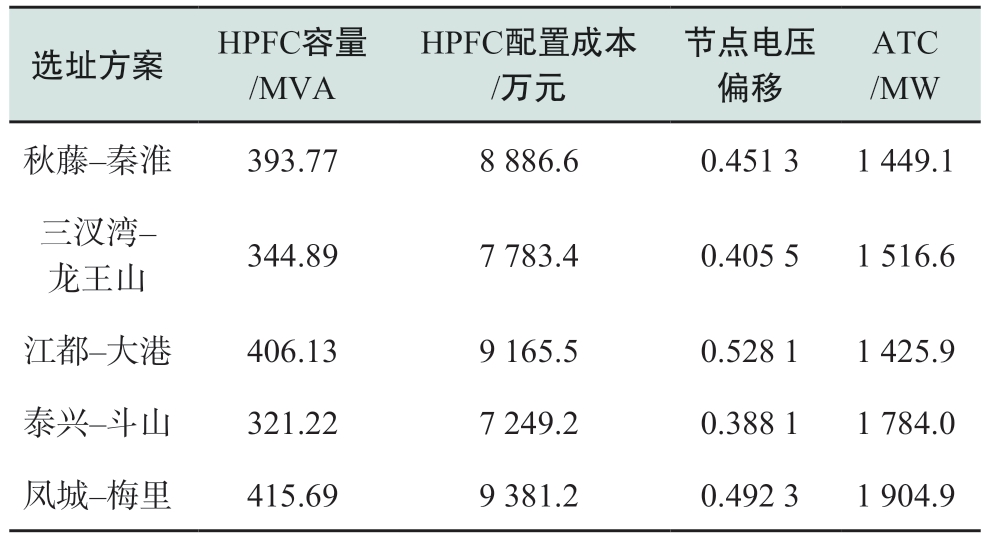
HPFC配置成本/万元选址方案 HPFC容量/MVA节点电压偏移ATC/MW秋藤–秦淮 393.77 8 886.6 0.451 3 1 449.1三汊湾–龙王山 344.89 7 783.4 0.405 5 1 516.6江都–大港 406.13 9 165.5 0.528 1 1 425.9泰兴–斗山 321.22 7 249.2 0.388 1 1 784.0凤城–梅里 415.69 9 381.2 0.492 3 1 904.9
从表2中可以得到,HPFC配置成本最少的是泰兴–斗山方案,相较其他选址方案最高可降低22.73%的配置成本,最低也可降低6.86%的配置成本。节点电压偏移最小的也是泰兴–斗山方案,相较其他选址方案最高可降低26.52%的节点电压偏移,最低也可降低4.29%的节点电压偏移。此外,泰兴–斗山方案的系统ATC相较于效果最好的凤城–梅里方案仅相差了6.35%。故泰兴–斗山方案的目标函数效果综合最好,因此选择泰兴–斗山线路作为HPFC的安装位置,对应的HPFC配置容量为321.22 MVA。
更近一步对比HPFC配置前后系统ATC和节点电压偏移情况,如图6所示。
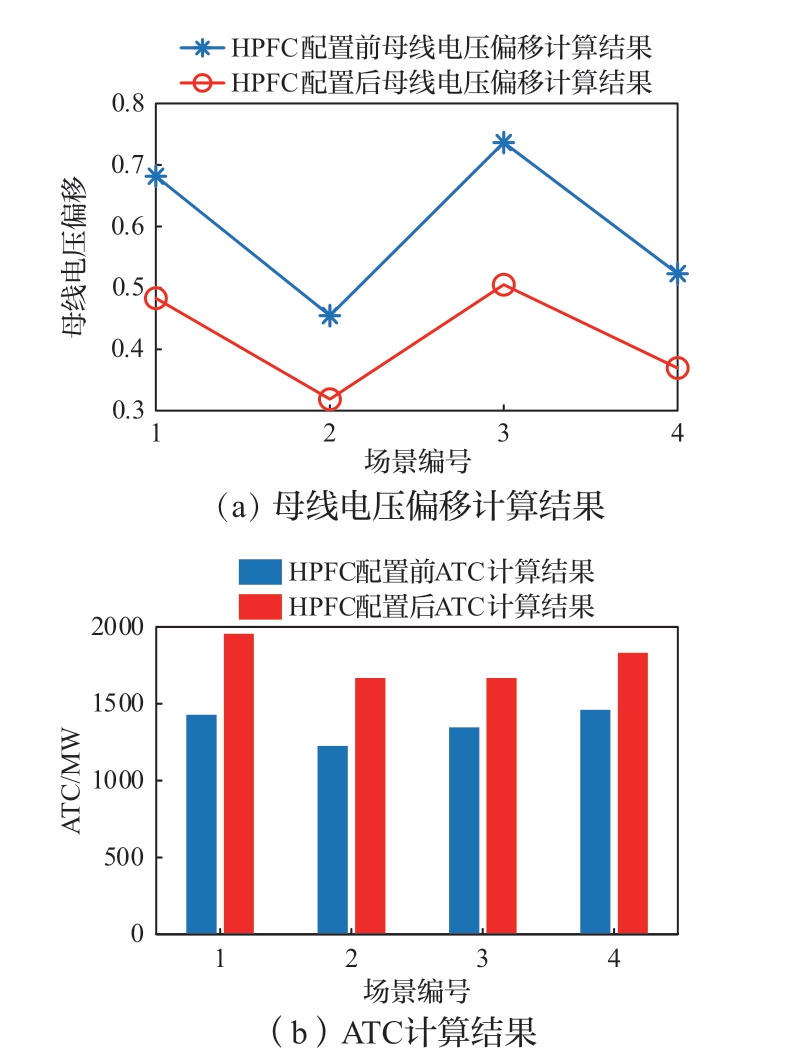
图6 HPFC配置前后不同场景下的系统ATC和节点电压偏移对比
Fig. 6 Comparison of system ATC and bus voltage deviation in different scenarios before and after HPFC configuration
从图6可以得到,在4个场景下节点电压偏移分别降低了29.12%、29.93%、31.42%、29.35%,系统ATC分别提升了36.90%、36.05%、23.80%、25.49%。这说明通过HPFC对系统潮流分布的调控,系统ATC和节点电压偏移都得到了明显的改善,充分体现出HPFC的控制效果。
4.3 不同优化配置方法对比
为了说明本文所提双层优化配置方法的优势,本节将另外采用单层优化配置方法进行HPFC容量配置计算,并与本文所提双层优化配置方法所得配置方案进行对比。单层优化配置方法以泰兴–斗山线路为HPFC安装线路,优化算法选择传统MOPSO算法,惯性权重设置为0.8,其余参数不变。两种方法计算得到的Pareto解集情况如图7所示。
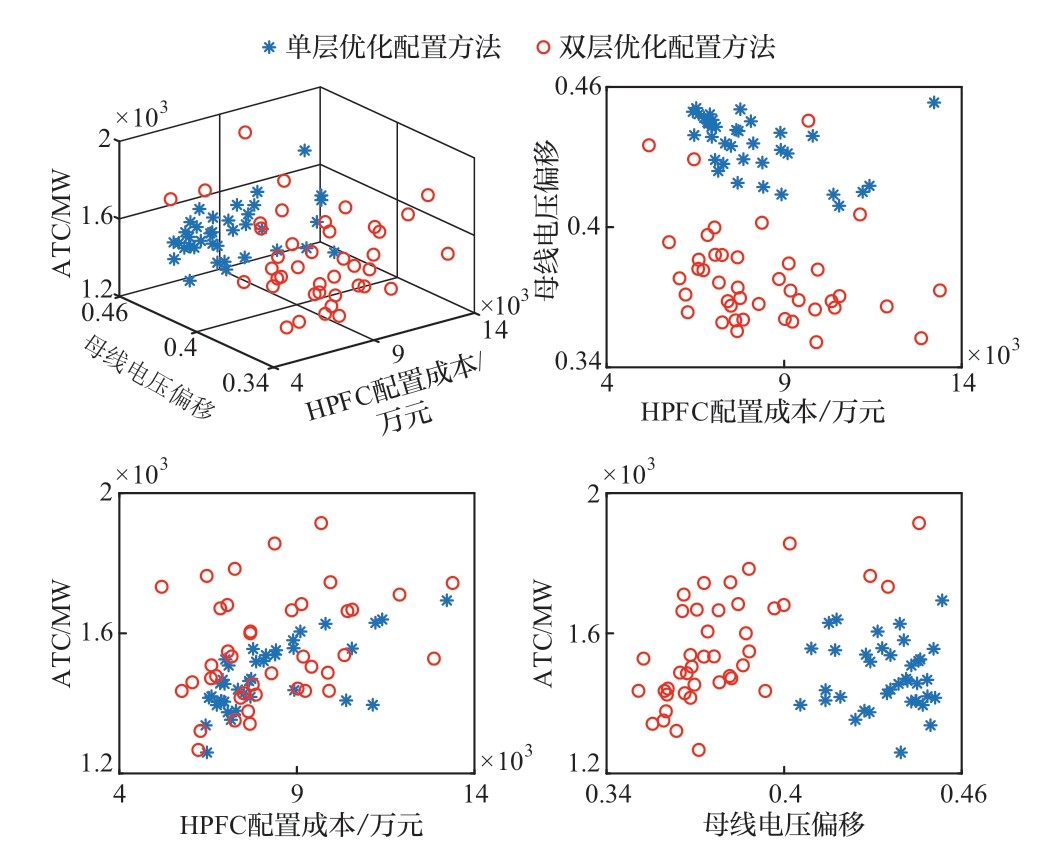
图7 不同优化配置方法的Pareto解集对比
Fig. 7 Comparison of Pareto solution sets for different optimization configuration methods
从图7可得看出,本文所提双层优化配置方法计算得到的节点电压偏移明显优于单层优化配置方法,而HPFC配置成本和ATC的范围相差不大。单层优化配置方法最终得到的折衷解如下:HPFC配置成本为8 410.1万元,节点电压偏移为0.417 2,ATC为1 552.0 MW。与单层优化配置方法所得折衷解相比,本文所提双层优化配置方法在HPFC配置成本方面降低了13.8%,在节点电压偏移方面降低了6.98%,在ATC方面提升了14.95%。本文所提双层优化配置方法得到的HPFC配置方案相比单层优化配置方法得到的HPFC配置方案对三个目标函数的优化效果都更好,说明本文所提方法能更好地指导HPFC的优化配置,验证了本文所提方法的有效性。
4.4 优化配置方法稳定性校验
考虑到MOPSO算法的随机寻优特性,为校验本文所提算法的稳定性,以泰兴–斗山线路为HPFC安装线路,采用本文所提双层优化配置方法重复进行10组试验,每组试验包括10次优化计算,选择模糊满意度最好的解作为该组试验的最终解,并统计各组试验最终解对应的目标函数计算结果,如表3所示。
表3 重复计算所得目标函数统计结果
Table 3 Statistical results of the objective function obtained from repeated calculations
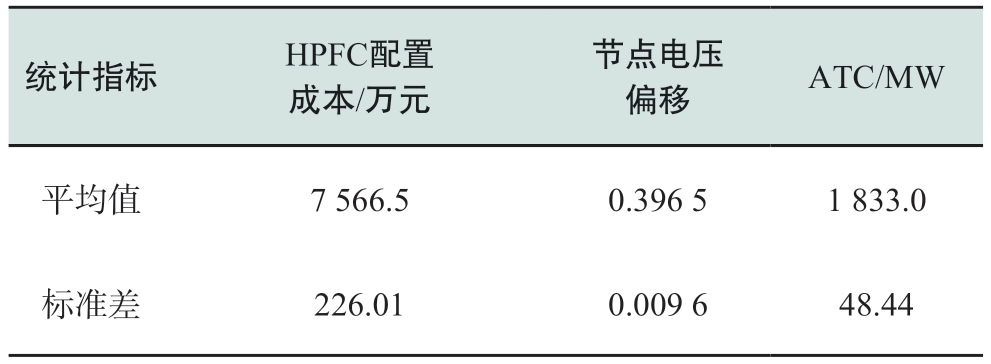
统计指标 HPFC配置成本/万元节点电压偏移 ATC/MW平均值 7 566.5 0.396 5 1 833.0标准差 226.01 0.009 6 48.44
从表3可以得到,各目标函数的标准差占平均值的比例分别为2.99%、2.43%、2.64%,均不超过3%,标准差均相对较小,说明本文所提双层优化配置方法具有较好的稳定性。
5 结论
本文提出了一种提升风电接入系统ATC的HPFC双层优化配置方法,研究了HPFC在江苏电网中的配置方案,并对比分析了所提方法与单层优化配置方法的效果以及所提方法计算结果的稳定性。结果表明,本文所提HPFC双层优化配置方法可以在获得HPFC在考虑风电/负荷不确定性情况下的最佳配置方案,有效改善系统ATC和节点电压偏移。与单层优化配置方法相比,本文所提方法所得到的HPFC规划配置方案具有更好的经济效益和功能性。此外,通过多次重复计算,验证了本文所提方法具有良好的稳定性。
参考文献
-
[1]
冀肖彤,杨东俊,方仍存,等. “双碳” 目标下未来配电网构建思考与展望[J]. 电力建设,2024,45(2):37-48.JI Xiaotong, YANG Dongjun, FANG Rengcun, et al. Research and prospect of future distribution network construction under dual carbon target[J]. Electric Power Construction, 2024,45(2): 37-48 (in Chinese). [百度学术]
-
[2]
陈逸文,赵晋斌,李军舟,等. 电力低碳转型背景下氢储能的挑战与展望[J]. 发电技术,2023,44(3):296-304.CHEN Yiwen, ZHAO Jinbin, LI Junzhou, et al. Challenges and prospects of hydrogen energy storage under the background of low-carbon transformation of power industry[J]. Power Generation Technology, 2023, 44(3): 296-304(in Chinese). [百度学术]
-
[3]
罗昊,王长江,王建国. 面向数字孪生的电-气综合能源系统可用输电能力计算[J]. 电力建设,2023,44(11):113-127.LUO Hao, WANG Changjiang, WANG Jianguo. Calculation of available transmission capacity of electricity-gas integrated energy system for digital twin[J]. Electric Power Construction,2023, 44(11): 113-127 (in Chinese). [百度学术]
-
[4]
陈艳波,王德帅,田昊欣,等. 基于源荷储协调运行的电网可用输电能力优化方法[J]. 电力系统保护与控制,2024,52(23):119-134.CHEN Yanbo, WANG Deshuai, TIAN Haoxin, et al. An optimal method for the available transfer capability of a power grid based on coordinated operation of source-load-storage[J].Power System Protection and Control, 2024, 52(23): 119-134(in Chinese). [百度学术]
-
[5]
LIU J A, LIU Y B, QIU G, et al. Learning-aided optimal power flow based fast total transfer capability calculation[J]. Energies,2022, 15(4): 1320. [百度学术]
-
[6]
CHAUHAN R, NARESH R, KENEDY M, et al. A streamlined and enhanced iterative method for analysing power system available transfer capability and security[J]. Electric Power Systems Research, 2023, 223: 109528. [百度学术]
-
[7]
MAJUMDAR K, ROY P K, BANERJEE S. Available transfer capability calculation of power systems using opposition selfish herd optimizer[J]. IETE Journal of Research, 2023,69(8): 5261-5275. [百度学术]
-
[8]
孙鑫,饶宇飞,肖浩,等. 基于线性化最优潮流的电网可用输电能力计算[J]. 电力自动化设备,2020,40(10):194-199.SUN Xin, RAO Yufei, XIAO Hao, et al. Available transfer capability calculation based on linearized optimal power flow[J]. Electric Power Automation Equipment, 2020, 40(10):194-199(in Chinese). [百度学术]
-
[9]
MÜHLPFORDT T, ROALD L, HAGENMEYER V, et al.Chance-constrained AC optimal power flow: a polynomial chaos approach[J]. IEEE Transactions on Power Systems,2019, 34(6): 4806-4816. [百度学术]
-
[10]
KOU X, LI F X. Interval optimization for available transfer capability evaluation considering wind power uncertainty[J].IEEE Transactions on Sustainable Energy, 2020, 11(1): 250-259. [百度学术]
-
[11]
AVILA N F, CHU C C. Distributed probabilistic ATC assessment by optimality conditions decomposition and LHS considering intermittent wind power generation[J]. IEEE Transactions on Sustainable Energy, 2018, 10(1): 375-385. [百度学术]
-
[12]
孙鑫,王博,陈金富,等. 基于稀疏多项式混沌展开的可用输电能力不确定性量化分析[J]. 中国电机工程学报,2019,39(10):2904-2913.SUN Xin, WANG Bo, CHEN Jinfu, et al. Sparse polynomial chaos expansion based uncertainty quantification for available transfer capability[J]. Proceedings of the CSEE, 2019, 39(10):2904-2913(in Chinese). [百度学术]
-
[13]
张大波,朱志鹏,连帅,等. 基于多场景变权多目标优化的UPFC在风电并网系统中的配置方案研究[J]. 电网技术,2019,43(2):638-645.ZHANG Dabo, ZHU Zhipeng, LIAN Shuai, et al. Allocation scheme research of UPFC based on multiple scenarios with different weighting coefficients and multi-target optimization in wind power integrated system[J]. Power System Technology,2019, 43(2): 638-645(in Chinese). [百度学术]
-
[14]
CHEN B C, FEI W L, TIAN C H, et al. Research on an improved hybrid unified power flow controller[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5649-5660. [百度学术]
-
[15]
陈柏超,曾永胜,刘俊博,等. 基于Sen Transformer的新型统一潮流控制器的仿真与实验[J]. 电工技术学报,2012,27(3):233-238.CHEN Baichao, ZENG Yongsheng, LIU Junbo, et al.Simulation and experimental research of a novel unified power flow controller based on Sen transformer[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 233-238(in Chinese). [百度学术]
-
[16]
YUAN J X, LIU L, FEI W L, et al. Hybrid electromagnetic unified power flow controller: a novel flexible and effective approach to control power flow[J]. IEEE Transactions on Power Delivery, 2016, 33(5): 2061-2069. [百度学术]
-
[17]
SADIQ A A, BUHARI M, ADAMU S S, et al. Coordination of multi-type FACTS for available transfer capability enhancement using PI–PSO[J]. IET Generation, Transmission &Distribution, 2020, 14(21): 4866-4877. [百度学术]
-
[18]
ADEWOLU B O, SAHA A K. Optimal setting of thyristor controlled series compensator with brain storm optimization algorithms for available transfer capability enhancement[J].International Journal of Engineering Research in Africa, 2022,58: 225-246. [百度学术]
-
[19]
GAUTAM A, IBRAHEEM, SHARMA G, et al. Available transfer capability enhancement in deregulated power system through TLBO optimised TCSC[J]. Energies, 2022, 15(12):4448. [百度学术]
-
[20]
ADEWOLU B O, SAHA A K. FACTS devices loss consideration in placement approach for available transfer capability enhancement[J]. International Journal of Engineering Research in Africa, 2020, 49: 104-129. [百度学术]
-
[21]
GUPTA D, JAIN S K. Available transfer capability enhancement by FACTS devices using metaheuristic evolutionary particle swarm optimization (MEEPSO)technique[J]. Energies, 2021, 14(4): 869. [百度学术]
-
[22]
CHEN Y B, WANG D S, LI J Q, et al. A SSSC optimal configuration method to enhance available transfer capability considering multi-wind farm access[J]. IET Renewable Power Generation, 2023, 17(16): 3777-3792. [百度学术]
-
[23]
WANG X T, WANG X Z, SHENG H, et al. A data-driven sparse polynomial chaos expansion method to assess probabilistic total transfer capability for power systems with renewables[C]//2022 IEEE Power & Energy Society General Meeting (PESGM). July 17-21, 2022, Denver, CO, USA.IEEE, 2022: 1. [百度学术]
-
[24]
袁佳歆,许顺凯,余梦泽,等. 一种配电网多线路混合式统一潮流控制器[J]. 电力工程技术,2023,42(1):1-10.YUAN Jiaxin, XU Shunkai, YU Mengze, et al. A multiline hybrid unified power flow controller for distribution network[J]. Electric Power Engineering Technology, 2023(1):1-10(in Chinese). [百度学术]
-
[25]
唐锦,张书怡,吴秋伟,等. 基于Copula函数与等概率逆变换的风电出力场景生成方法[J]. 电力工程技术,2021,40(6):86-94.TANG Jin, ZHANG Shuyi, WU Qiuwei, et al. Wind power output scenario generation method based on Copula function and equal probability inverse transformation[J]. Electric Power Engineering Technology, 2021, 40(6): 86-94(in Chinese). [百度学术]
-
[26]
雍静,赵瑾,郇嘉嘉,等. 基于混沌增强烟花算法的多能源系统并网优化调度[J]. 电网技术,2019,43(10):3725-3733.YONG Jing, ZHAO Jin, HUAN Jiajia, et al. Multi-energy system optimal dispatch based on chaos enhanced firework algorithm in grid connection[J]. Power System Technology,2019, 43(10): 3725-3733(in Chinese). [百度学术]
基金项目
国网江苏省电力有限公司科技项目(J2023150)。
Science and Technology Foundation of State Grid Jiangsu Electric Power Co., Ltd. (J2023150).


