0 引言

为实现“碳达峰”和“碳中和”的目标，建立以可再生能源为主导，多能互补的能源体系势在必行[1-6]。然而，以风电、光伏为代表的可再生能源大量接入电网，会显著改变电网的动态特性，导致新的安全稳定问题。其中，以电力电子变流器为接口的可再生能源设备与电网之间的动态相互作用所产生的振荡问题极为关键，需要对其进行详细分析，以保障电力系统安全稳定运行[7-11]。

由于电力系统的运行方式具有多样性和复杂性，其运行状态可能因负荷波动、发电机组投切、网络拓扑变化以及外部环境因素而频繁调整。因此，在对电力系统进行振荡稳定分析时，必须充分考虑多种运行工况的影响。振荡稳定域作为一种重要的分析工具，被定义为系统参数组合与振荡稳定性之间的映射关系。它能够全面反映系统在不同运行工况下的振荡稳定性特征，为电力系统规划和运行人员提供直观且科学的决策支持。具体而言，振荡稳定域通过将系统关键参数（如发电机出力、负荷水平、网络阻抗等）作为变量，构建出一个多维空间中的稳定边界。在这一空间中，稳定区域和不稳定区域被明确划分，从而帮助运行人员快速识别系统在不同工况下的稳定裕度。例如，在新能源大规模接入的背景下，振荡稳定域可以用于评估风电场或光伏电站并网后对系统振荡特性的影响，为优化运行方式提供依据[12-13]。

现有的振荡稳定域构建方法主要有：①逐点分析法；②基于圆盘定理的构建方法；③基于预测矫正法的安全域构建方法；④基于随机森林分类的振荡稳定域构建方法。

逐点分析（遍历）法在安全域参数空间内，基于特征值分析或时域仿真等方法判断系统在各参数组合下的振荡稳定性，通过遍历整个参数空间，得到所有振荡临界稳定点，连接构成振荡稳定域边界[14-17]。逐点遍历法的准确性受到待分析参数组合区域及采样步长的影响，为保证安全域边界的准确性，需要对参数空间大量密集采样。考虑到风电并网系统模型阶数高，振荡模式多，采用逐点遍历法计算量会非常大，效率低，耗时长。

基于圆盘定理的安全域边界构建方法[18]首先对状态空间矩阵特征值的分布范围进行估计，并依据系统稳定条件对含参的特征值分布范围进行限定，进而通过逆过程构建安全域。该方法只需使用基本圆盘定理对状态矩阵特征值范围进行估计，进而构建安全域，与逐点遍历法相比，大幅提升了计算效率，但是所构建的安全域有一定保守性。

基于预测矫正法的安全域边界构建方法[19-20]在原有逐点遍历法的基础上加以改进，利用相邻边界点距离相近的特点，在上一个边界点的附近搜索下一个边界点，可以大大减少搜索次数，提高搜索效率。然而，由于预测矫正法本质上仍需搜索出安全域边界，当考虑的变量数更多时，所需搜索的边界点的数目呈指数规模增长，导致该方法计算量会非常大，效率低，耗时长。

基于随机森林分类的振荡稳定域构建方法[21]首先通过获取不同工况下的振荡分析结果，得到数据集并采用随机森林分类器得到振荡稳定域。然而，该方法具有一定的随机性，应用在不同系统中的准确性有待进一步验证。

综上所述，现有振荡稳定域构建方法均存在一定的不足。本文基于多层感知机回归方法构建电力系统稳定域，相较于传统方法，所提方法在建模精度、计算效率和适用性方面具有显著优势。传统方法通常依赖于逐点分析或边界搜索，存在计算复杂度高、对高维稳定域适应性差等问题，难以满足大规模电力系统多工况下的快速分析需求。而本文提出的方法通过结合机器学习技术，能够有效克服这些局限性，为电力系统稳定域的构建提供一种高效且精确的新途径。具体贡献如下：根据振荡稳定性判据，将振荡稳定性区域定义为一个参数空间；进而提出一种基于改进多层感知机（multi-layer perceptron，MLP）的电力系统稳定域构建方法，与传统MLP相比，所提方法在模型结构、训练算法和数据处理方面进行优化，通过引入正则化技术和自适应学习率，提升模型的泛化能力；通过特征选择和降维处理，降低输入数据的维度，进一步提高计算效率；通过宁夏电网中某实际新能源接入系统验证所提方法的有效性，表明该方法精确且计算效率高。

1 振荡稳定域定义及其构建

1.1 振荡稳定域定义

电力系统的运行方式复杂多变，并且电力系统中振荡稳定性受多种因素影响。振荡稳定域的构建主要针对振荡的关键影响因素，分析关键影响因素对振荡的影响。同时，振荡稳定域能够在系统运行条件发生变化时，无需重新建模分析即可得到系统振荡稳定性分析结果，为振荡风险的在线评估提供了便利。

振荡稳定性的判断标准为系统中是否存在负阻尼的振荡模式。由于设备控制参数往往在电力电子设备接入后系统运行过程中不再改变，因而对于振荡稳定域的应用，一般定义在运行空间，通常选出电力系统运行过程中对振荡影响较大的运行变量，如新能源机组输出功率、线路串补度、短路比等。根据所选各变量的取值范围S，以及各变量下的振荡阻尼，定义振荡稳定域如下：

式中：x表示系统中的各工况变量；σ(x)表示变量x下的阻尼。

当系统中影响变量过多时，向量x的维数很高，稳定域构建复杂。因而，此时需要采用特征提取方法，如采用最大相关性-最小冗余性（max-relevance and min-redundancy，mRMR）方法[21]，通过变量与稳定性之间的相关性选取参数，且保证所选变量足以描述大多数工况下对应的稳定性，使得在保证一定的准确性的前提下，具有较低的计算量。

1.2 振荡阻尼计算

振荡稳定问题本质为小扰动稳定问题[22]。分析方法基于小信号模型，如线性化状态空间模型和阻抗模型，可通过线性化微分代数方程进行推导。然后通过小信号模型建立电力系统的特征方程，特征方程直接用数值方法求解。当特征方程有一个实部为正的根时，则该根对应一个不稳定振荡模式。振荡的发散比和频率与实部为正的根的实部和虚部相对应。

文献[23]采用对数导数法以实现振荡稳定性的定量分析。通过聚合阻抗方法，得到表征系统动态特性的闭环传递函数Δ(s)的频率特性曲线Δ(ω)，然后通过频域方法辨识得到该传递函数的主导零点，主导零点求解方式如下。

若在频率ωz下，Δ(ω)对数导数实部出现极值点，且对数导数虚部斜率为负，则在该频率下有一零点z=αz+jωz，实部αz可以通过对数导数实部求解得到。振荡模式的阻尼σ可以定义为-αz，当存在某个振荡模式的阻尼小于0，则表示其对应振荡模式不稳定。

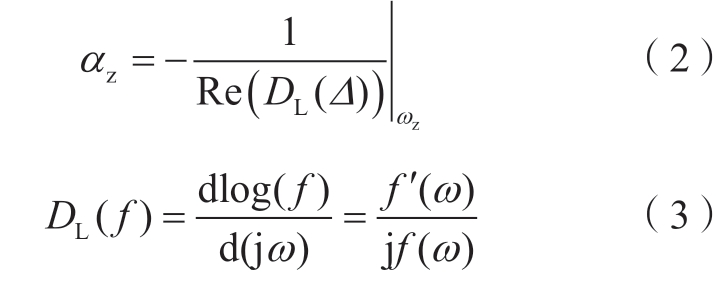
2 基于改进多层感知机回归的振荡稳定域构建

稳定域构建问题的核心在于建立工况变量与系统稳定性之间的映射关系。然而，这种关系通常极为复杂，难以通过理论推导获得精确的解析表达式。因此，数据驱动的方法成为解决这一问题的有效途径。传统的稳定域构建方法，如逐点计算或边界搜索，往往计算效率较低且精度有限。相比之下，人工智能方法能够充分利用有限的数据，高效拟合工况变量与稳定性之间的复杂关系，在保证较高计算效率的同时，显著提升预测的准确性。

2.1 数据集获取

2.1.1 蒙特卡洛方法

为了训练多层感知机，通常需要一个标注数据集，其中每个数据点都与相应的目标输出相关联。为获取数据集，在所选各参数的取值范围S内随机选点，并计算出所有点对应工况下系统的各振荡模式阻尼的最小值。在训练多层感知机之前，确保对数据集进行了适当的预处理，并将其分成训练集和测试集。

2.1.2 数据增强

在数据集中，往往会存在稳定数据和不稳定数据不平衡、数据量不足等问题。为解决该问题，可采用数据增强技术。它通过对训练数据集进行一系列随机或确定性变换，生成新的数据样本，其具体目的如下。①提高模型的泛化能力：通过增加数据集的多样性，使得模型在面对从未见过的数据时仍能做出准确的预测。②防止过拟合：扩展数据集的规模，使得模型不会因为过度记忆训练集而影响对新数据的预测能力。③弥补数据不足：获取足够多的标注数据往往很难，数据增强可以在一定程度上缓解这个问题。本文具体采用合成少数过采样技术（synthetic minority over-sampling technique，SMOTE）[24]实现，能够较好地处理数据不平衡、数据量不足等问题。

2.2 多层感知机模型

2.2.1 模型结构

多层感知机通常也称为人工神经网络，其示意图如图1所示。它由多层节点（神经元）组成，一层中的每个神经元都与下一层中的每个神经元相连。输入层接收输入数据，然后通过一个或多个隐藏层，最后到达输出层。MLP可以有多个隐藏层，从而能够学习数据中的复杂模式，是用于各种任务（如分类、回归和深度学习中更复杂的问题）的通用模型。

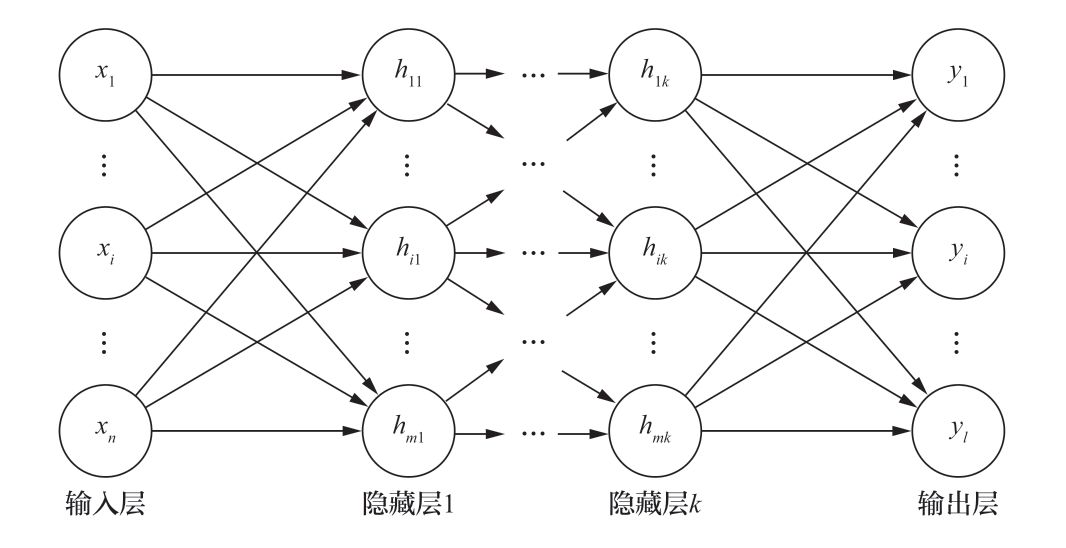
图1 多层感知机示意图
Fig. 1 The diagram of multi-layer perceptron

单个神经元的工作原理如图2所示。神经元的输入为前一层的输出乘以连接权重之和，并使用激活函数f(s)为模型引入非线性。激活函数f(s)有很多种选择，比如Sigmoid、tanh、ReLU函数。本文具体采用的是ReLU函数，其优势在于：①易于收敛，不会出现梯度饱和、梯度消失的问题；②计算复杂度低，不需要进行指数运算，只要一个阈值就可以得到激活值。

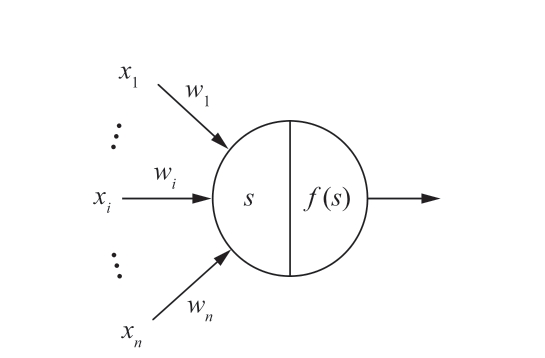
图2 单个神经元工作原理
Fig. 2 The operating principle of perceptron

2.2.2 前向-反向传播过程

多层感知机的前向传播过程即为输入层到输出层的函数，式 （4） 为隐藏层数为2时的前向传播函数。

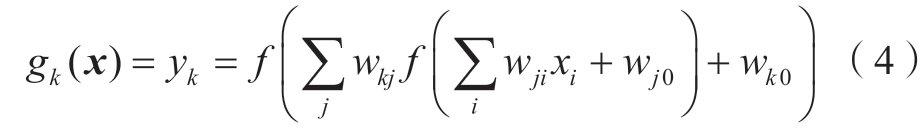
式中：x为输入层的输入；wji为连接权重；yk为输出。

在训练过程中，网络会使用反向传播和梯度下降等方法调整神经元之间的连接权重，以尽量减小预测值和实际输出值之间的误差E：

式中：为实际多层感知机的输出；yj为目标输出，由数据集确定。

对于节点神经元j，误差关于权重的偏导数可以由式 （6） 计算：

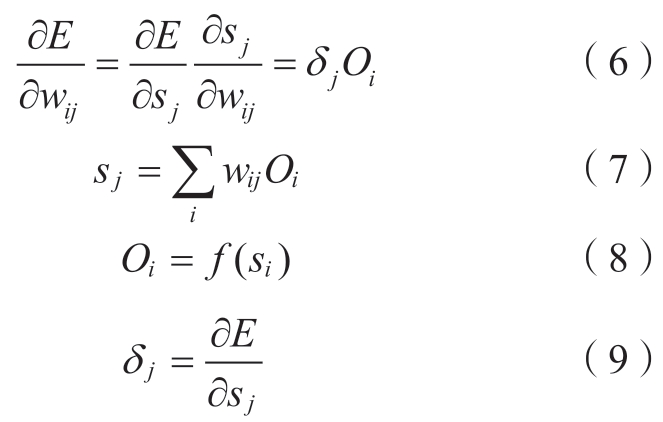
式中：wij为前层神经元i与该神经元j之间的连接权重；神经元输入加权和sj、神经元输出Oi以及δ j的定义分别如式（7）、（8）、（9）。

如果节点j为输出层节点，δ j的计算方式如式（10） 所示；如果节点j为隐藏层节点，可以根据该隐藏层之后一层的δk和两者之间连接权重wjk计算得到，其计算方式采用式（11）。

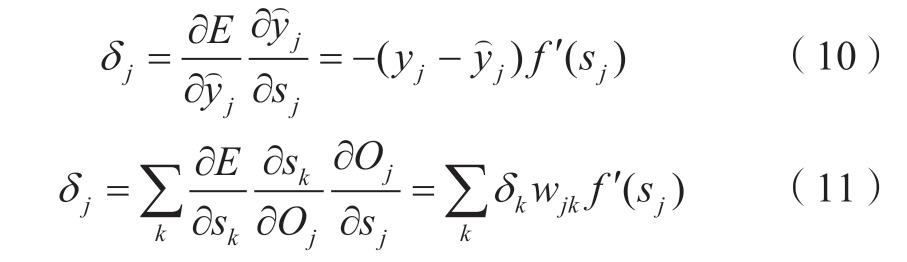
根据式 （6） 设置步长，改变权重值：

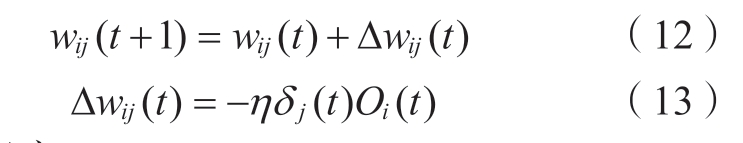
式中：η为学习率。

通过从输出层逐步反向计算各层的连接权重wij，神经元输入加权和sj、神经元输出Oi以及δ j，通过式（12）、（13）逐层调整权重，即实现反向传播过程。重复前向-反向传播过程，直到得到较小的误差E，输出多层感知机模型。

2.3 改进多层感知机模型

通过改进多层感知机，可以显著提高其性能和泛化能力。主要的改进方向包括：超参数优化、引入正则化方法、自适应优化算法、权重初始化。

2.3.1 神经网络超参数优化

采用神经网络超参数优化以获取最优超参数来实现网络性能提升，具体步骤如下。

1） 穷举搜索：定义一个参数网格，其中包含模型超参数的多个可能取值组合。

2） 交叉验证：对每一组参数组合，模型都会通过交叉验证进行训练和评估。这有助于确保模型性能的可靠性，而不是过拟合到特定的训练集上。

3） 参数优化：在评估所有参数组合之后，返回所选择的评估指标（如准确率等）的最佳参数组合。

2.3.2 L2正则化

L2正则化（也称作权重衰减）通过对MLP各层损失函数添加权重的平方和的惩罚项，防止模型参数变得过大，从而减少过拟合。

式中：λi是正则化系数；wi为MLP各层神经元权重。

2.3.3 自适应优化算法

在反向传播过程中，传统的梯度下降算法，如随机梯度下降（stochastic gradient descent，SGD）在训练复杂模型时往往收敛较慢，因此可以使用一些更先进的自适应优化算法。本文采用自适应动量估计（adaptive moment estimation，Adam）方法[25]，其结合了动量法式 （15） 和RMSProp式 （16），能够在不同维度上对学习率进行自适应调整，从而通常表现出比传统SGD更快的收敛速度和更好的稳定性。

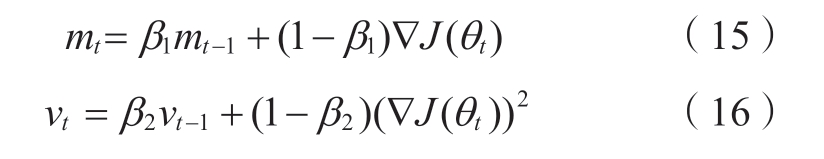
式中：θt是超参数；mt是梯度的一阶矩估计；β1是动量衰减率，通常默认设置为0.9；vt是梯度的二阶矩估计；β2是加速度衰减率，通常默认设置为0.99。

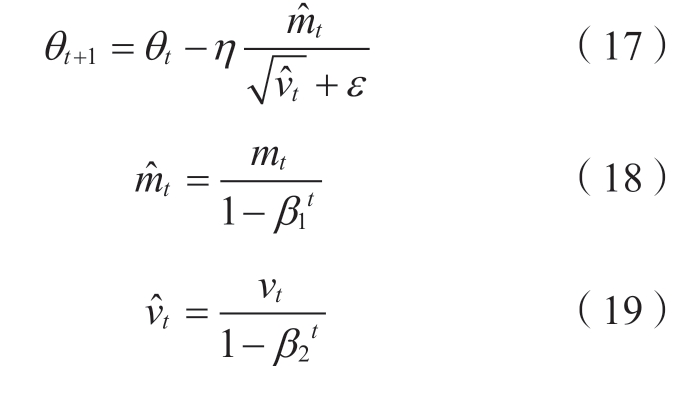
式中：ε是一个小常数，通常取10-8。

2.3.4 He初始化权重

He初始化是一种针对ReLU激活函数的权重初始化方法[26]。该方法通过随机分布生成权重，确保权重的方差适中，保持网络每层的输入和输出方差一致，能够避免初始权重过大或过小导致的梯度消失或爆炸问题。

2.4 基于改进多层感知机回归的稳定域构建

步骤1：He初始化权重，t=0。

步骤2：采用蒙特卡洛法获取训练数据集，即参数{x1, x2, …, xn}对应电力系统各振荡模式的最小阻尼{y1, y2, …, yn}，并进行数据增强。

步骤3：利用前向数据集参数{x1, x2, …, xn}，进行式 （4） 前向计算，得到MLP输出。步骤4：从输出层各神经元开始，向左逐层调整权重。如果节点j为输出层节点，采用式 （9） 计算；如果节点j为隐藏层节点，采用式 （11） 计算。采用Adam方法更新学习率，采用式 （13） 调整权重。

步骤5：通过超参数优化的方法获取多层感知机模型的最优参数组合。如果误差E达不到预设阈值或者迭代步数少于预设步数，则返回步骤3重新调整权重；反之，则输出多层感知机模型。

步骤6：在所选参数取值范围所构成的参数空间内，设置较小的步长来选取，绘制参数关于阻尼是否大于0的散点图，并取散点图的凸包截面，从而得到稳定域图像。

3 算例分析

3.1 某实际新能源并网系统

图3为宁夏电网中某330 kV新能源汇集站的接线图。该新能源场站下属包括3个风电场（A、B、C）和5个光伏电站（A、B、C、D、E），总计新能源装机容量为1220 MVA。由于该汇集站新能源的集中接入，需要对该汇集站所处新能源并网系统的振荡风险进行评估，得到系统的振荡稳定域。

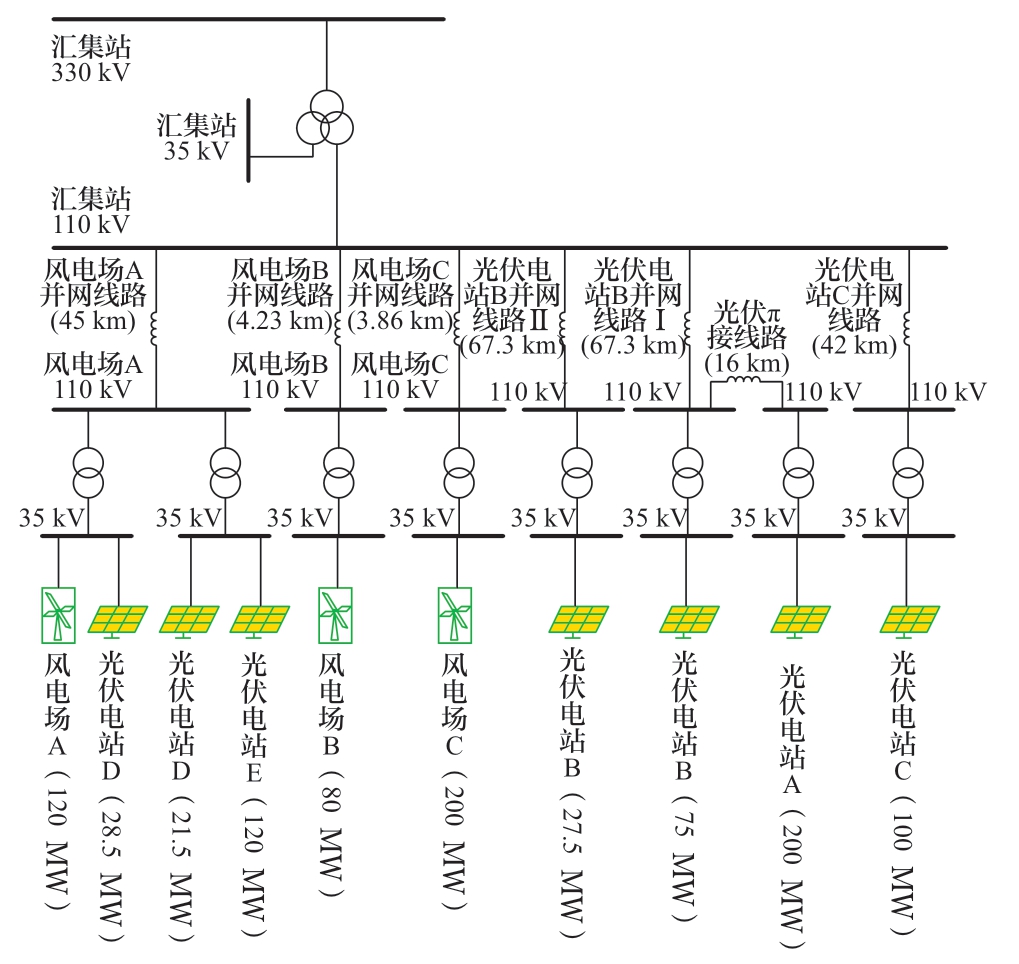
图3 新能源汇集站接线
Fig. 3 The diagram of a new energy integrating station

3.2 稳定域构建

在新能源并网系统运行过程中，随着风速和系统运行方式的变化，其新能源场站的机组台数和机组输出功率也在不断变化。因而机组台数N、机组输出有功功率P、输出无功功率Q为自变量，构成系统工况空间，采用改进的多层感知机分类器构建振荡稳定域。本节为了稳定域展示，仅取单个新能源场站（风电场A）的N、P、Q作为自变量，对于多个新能源场站的稳定域分析，可以将各新能源场站的N、P、Q增加到稳定域变量中进行分析。

首先采用蒙特卡洛方法在工况空间进行采样，机组台数N和机组输出有功功率P取值范围均为0~1 pu。考虑到功率因数范围一般为±0.9，这里无功功率Q取值范围为-0.5~0.5 pu。选取的工况数为1000。采用阻抗法分别计算系统在这些工况点的主导振荡模式阻尼，将工况及其对应阻尼作为数据集进行训练。然后将这些点输入多层感知机模型，并采用He权重初始化、自适应优化算法、超参数优化等方法进行模型优化，得到能够实现振荡稳定分类的模型。在整个空间上均匀取点，根据这些点的振荡稳定性，取这些点的凸包为不稳定区域，如图4中深蓝色区域所示。

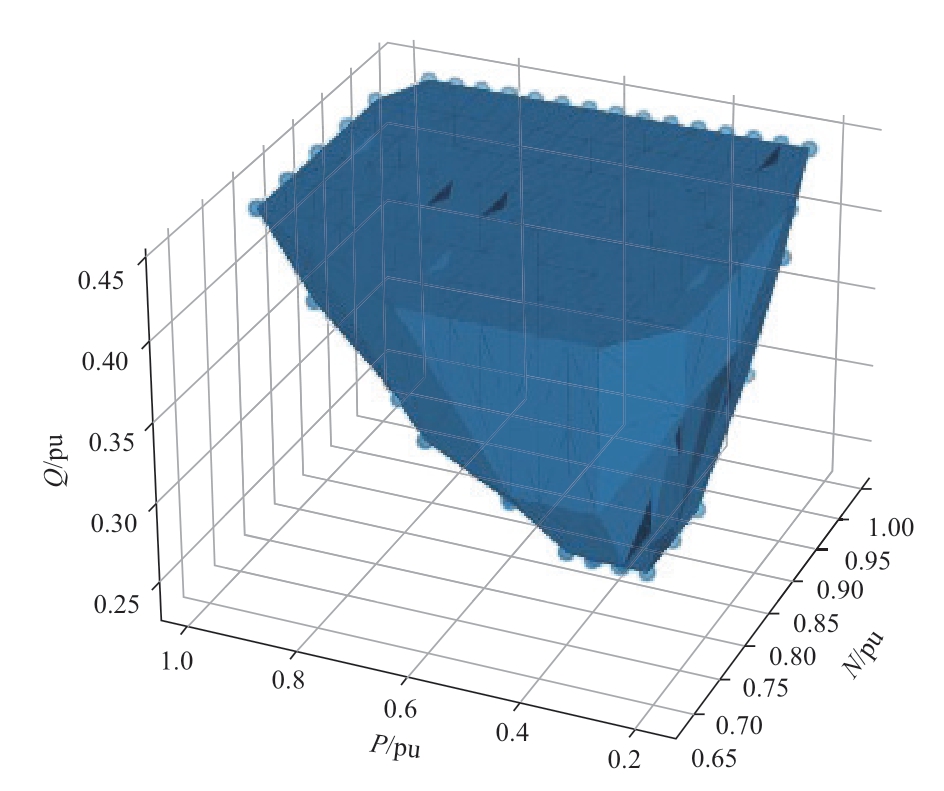
图4 新能源接入系统振荡不稳定区域
Fig. 4 System’s oscillatory instability region

根据不稳定区域结果，机组台数N越大，不稳定区域越大，系统越容易发生振荡。无功功率Q增大到0.25 pu时，系统在P=0.4 pu、N≥0.8 pu时，会出现振荡现象。随着Q的增大，不稳定区域增大，系统振荡风险增大。对于有功功率P，其大小和振荡风险大小为非线性关系，当P在0.4 pu左右时，不稳定区域最大，但相对来说P的变化对振荡稳定的影响没有Q或N影响大。

3.3 准确率和计算效率验证

为了说明该方法的有效性，在训练集和测试集上计算该方法的准确率。训练得到的模型在训练集中的准确率为97.4%，在测试集的准确率为97.6%，两者差异不大且均达到了较高水平，所提方法的有效性得到了验证。

作为对比，直接采用2.2节未改进的多层感知机模型，采用传统的随机梯度下降法进行训练，最大迭代次数同样设置为1000，分析得到的模型在训练集和测试集上的准确率分别为95.5%和96.0%。该准确率小于改进后的多层感知机模型，说明2.3节的改进方法能够有效提高模型的准确性。

计算效率方面，所提方法需计算1000组随机选取的工况点，训练得到振荡稳定域，变量之间精度可达0.01 pu。测试得到计算1331组工况点所需时间为728.78 s，即平均单组工况点振荡分析时间为0.547 5 s。所提方法数据获取时间为547.50 s，且训练时间仅为4.84 s，整体计算时间为552.34 s。而采用传统逐点计算方法，为达到相同精度的稳定域，其所需计算的工况点为1003组，估算得到数据获取时间为5.475×105 s，远远高于所提方法，从而验证了所提方法计算效率高。

4 结论

MLP作为一种非线性神经网络模型，能够有效地捕捉复杂系统中输入变量和系统稳定性之间的非线性关系。MLP在预测电力系统的振荡稳定边界方面具有高效、准确、数据驱动等优势。本文在MLP的基础上进行改进，引入了数据增强、自适应优化算法、超参数优化、权重初始化等方法进行优化，实现了模型准确率和泛化能力的提升。通过宁夏电网中某系统验证了该方法的有效性，测试数据集中稳定域的准确率高达97.6%，且模型训练时间仅为4.84 s。

后续工作将会结合其他机器学习技术（如卷积神经网络、长短期记忆网络等）进一步提升模型性能；在模型训练中引入更多的实际工况数据，增强模型的实际应用能力；开发更轻量化的模型，适应实时在线监控系统的需求。