Enhanced interconnection and damping assignment passivity-based control for PM synchronous motors

0 Introduction

Permanent Magnet Synchronous Motors (PMSMs)have established themselves as a leading technology in electric propulsion systems due to their high efficiency, elevated power density, excellent dynamic response, and low maintenance requirements.Their widespread application across various industrial sectors—such as electric vehicles,aerospace, and renewable energy—highlights their critical role in the evolution of modern electromechanical systems[1].Despite these advantages, PMSMs also introduce significant control challenges stemming from their nonlinear dynamics.These nonlinearities are primarily caused by time-varying system parameters and unpredictable load torque disturbances, which can result in performance degradation, DC-link voltage fluctuations, and even potential instability in the drive system [2,3].

Achieving high-performance control of PMSMs while ensuring robustness and maintaining implementation simplicity remains an active research challenge.Conventional control strategies, such as PI control, are often insufficient in coping with system uncertainties and dynami c variations.To address these limitations, a wide range of advanced nonlinear control strategies have been explored,including sliding mode control [4], model predictive control [5], and active disturbance rejection control [6].These methods have demonstrated enhanced dynamic performance and improved robustness under uncertainty.Nonetheless, many of these approaches involve complex control laws or requir e precise system modeling and tuning, which can limit their applicability in real-time industrial settings.

In this context, energy-based control strategies have attracted increasing attention due to their systematic and physically motivate d approach to nonlinear system control.Developed within control theory [7,8], IDAPBC has demonstrated effectiveness in diverse applications, including robotic systems [9-11], aerial vehicles such as UAVs and VTOL platforms [12,13], and advanced power systems involving AC/DC microgrids and power electronics [14,15].A key strength of the PCH methodology lies in its ability to preserve the energy-based structure of the system in the closed-loop configuration.By employing IDA-PBC framework, it is possible to design controllers that ensure system passivity while using the closed-loop energy function directly as a Lyapunov function.This facilitates both controller synthesis and stability analysis.In recent studies, IDA-PBC has been effectively applied to PMSM drives for speed control under known and unknown load torque conditions [16-19].However, these approaches generally assume precise knowledge of system parameters and do not fully account for real-world uncertainties such as time-varying loads or parameter drifts.

Motivated by these considerations, this paper proposes a novel control approach that integrates a nonlinear disturbance observer with the IDA-PBC framework to enh ance the robustness and dynamic performance of PMSM drive systems.The main contributions are as follows:

Enhanced Robustness: A nonlinear disturbance observer is incorporated to estimate lumped mismatched disturbances, including parameter variations and external load torques, enabling feedforward compensation.

Simplicity and Practicality: The control structure remains relatively simple, with a limited number of tunable parameters, facilitating practical implementation.

Hamiltonian-Based Structure: Preserves the PCH framework, which supports systematic stabili ty analysis and energy-based consistency.Improved Dynamic Performance: Integrates derivatives of desired state variables to achieve faster transient response and more accurate tracki ng of timevarying references, crucial for high-performance PMSM drives.

The paper is structured as follows.First, we provide a concise overview of Hamiltonian energy control modeling,the chosen control strategy, and the state observer design.Following this, we present a detailed model of the PMSM drive syste m.The core of the paper then delves into the proposed Hamiltonian control approach, which is enhanced with online parameter estimation using a state observer.

Finally, the proposed control strategy is validated via simulation and experimental results under varying operating conditions, with comparisons made against a classical control strategy based on PI controllers.Thi s is accompanied by a comprehensive discussion providing an in-depth analysis of the effectiveness of the proposed approach.

1 Hamiltonian modeling and control of PMSM

1.1 Interconnection and damping assignment passivity-based control: IDA-PBC

The IDA-PBC methodology (also known as Hamiltonian energy control) offers a structured and physically grounded approach for the synthesis of nonlinear controllers.Its core principle lies in shaping a desired stored energy function, also referred to as the Hamiltonian function, denoted aswhich reaches its minimum at the desired equilibrium point or reference sta texref, while maintaining energy balance throughout the system dynamics.Originally developed for Port-Controlled Hamiltonian(PCH) systems represented in the canonical form (1), the IDA-PBC framework has been rigorously formalized,where a step-by-step procedure for constructing, along with necessary conditions for interconnection and dissipation matrices, is detailed.

Although the IDA-PBC framework was initially tailored to systems that naturally exhibit a Hamiltonian structure, its applicability extends to a broader class of nonlinear systems beyond the PCH formalism, as demonstrated in[7,8].The general form of a PCH system is given by:

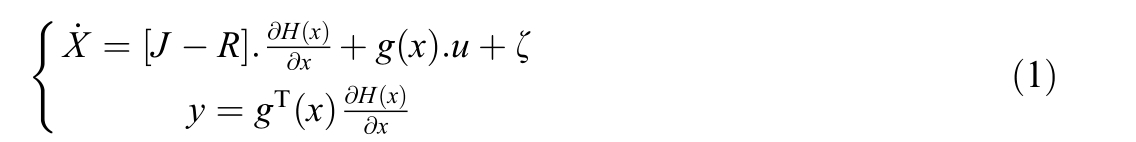
Accordingly, the desired closed-loop dynamics under the IDA-PBC framework are expressed as:

To synthesize the control input u, one must enforce equivalence between the desired closed-loop dynamics (2)and the actual open-loop system representation (1).This leads to the foll owing matching equation:

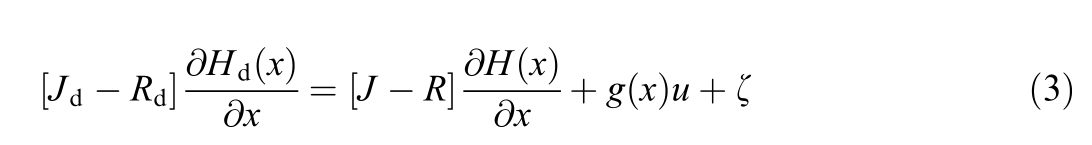
Subsequently, we can derive the foll owing control law:

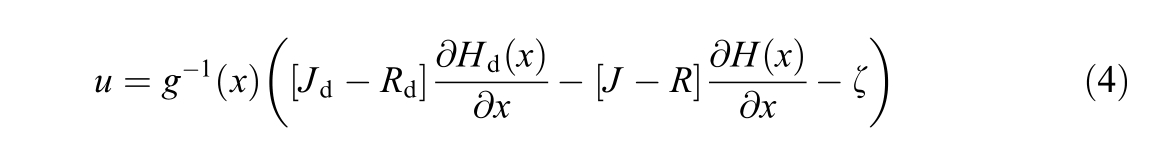
By leveraging the principles of Lyapunov theory, the IDA-PBC methodology ensures that the control led output variable achieves global asymptotic convergence [7,8].

1.2 Enhanced interconnection and damping assignment passivitybased control: IDA-PBC

In real-world applications, the desired equilibrium point for a system like a PMSM drive is unlikely to remain constant but evolves over time in response to varying operational conditions such as load fluctuations or changing speed commands.Additionally, very slow changes might not be desirable for applications requiring fast response times.To address this challenge, we introduce the concept of tracking error,denoted byThis error represents the deviation between the actual system state and the desired,time-varying,equilibrium point.Furthermore,the rate of change of the tracking error, e, is also relevant for control design.

Considering the non-constant nature of the desired equilibrium point, the closed-loop Hamiltonian control can be further expressed as:

We have established that the desired equilibrium point, denoted by xrefexhibits global exponential stability.This ensures that the system states xconverge exponentially to xref regardless of the initial conditions.Importantly, xref serves as the reference trajectory for the actual state vector x,and its evolution is governed solely by external inputs or disturbances.As a result,x refremains decoupled from the internal system dynamics, leading to the following formulation:

Then, the closed-loop system dynamics, considering the time-varying nature of the reference traje ctory, can be reformulated in the PCH framework as follows:

The new control law u can be calculated by:

This modified control law explicitly accounts for the non-static behavior of the desired state, thereby enhancing the system’s ability to track dynami c reference trajectories while preserving the passivity-based structure of the original control formulation (Fig.1).

1.3 PMSM drive plant model

The studied system consists of a non-salient pole threephase Permanent Magnet Synchronous Machine (PMSM)supplied by a Voltage Source Inverter (VSI).A schematic representation of the system is provided in Fig.2.The dynamic behavior of the system can be described in the rotating d-q reference frame using the following equations:

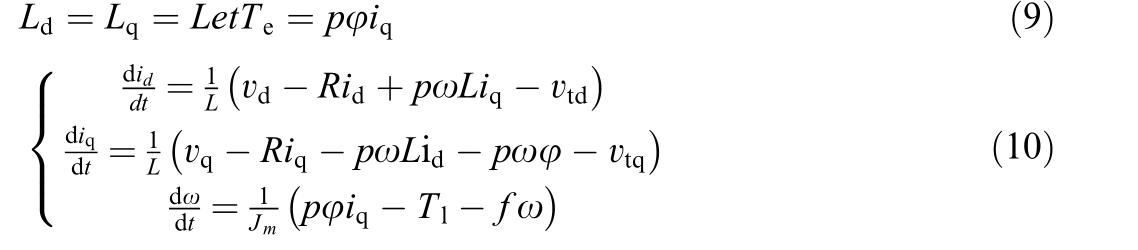
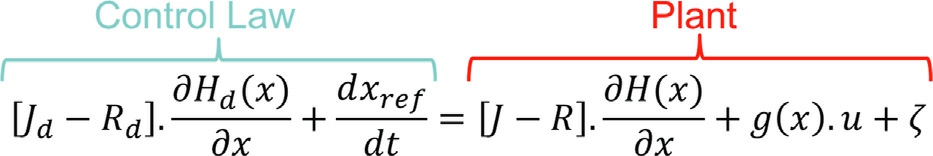
Fig.1.Concept of the Hamiltonian energy control or passivity control.

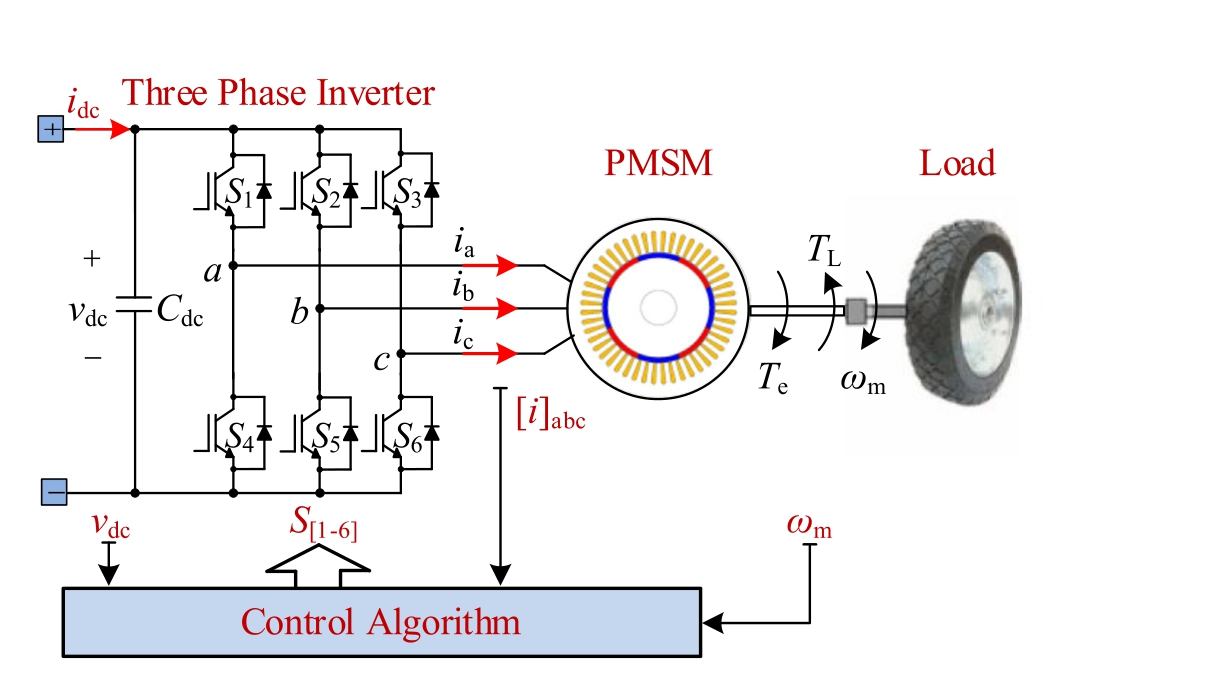
Fig.2.Three-phase PMSM driving system.

where vd and v qare the direct and quadrature motor voltages (V), id an d i q are the direct and quadrature motor currents (A), p is number of pole pairs, ωis the mechanical angular frequency (Rad/s), φ isthe permanent magnet flux linkage (Wb), Te is the electromagnetic torque (Nm), Tl is the load torque (Nm), f is the friction coefficient (Nmss/rad), Jmis the moment of inertia of the rotorR is the resistance of motor (Ω), Ldand Lq are the d and qaxis inductance (H) respectively.

vtd and vtqrepresent respectively the d and q-axis voltage drops (V) within the permanent magnet synchronous motor (PMSM) and inverter.These voltage drops account for various power losses that occur during motor operation.

To reformulate the PMSM drive system in the PCH form as described by equation(1), we define the state variable, input and output as follows, respectively:

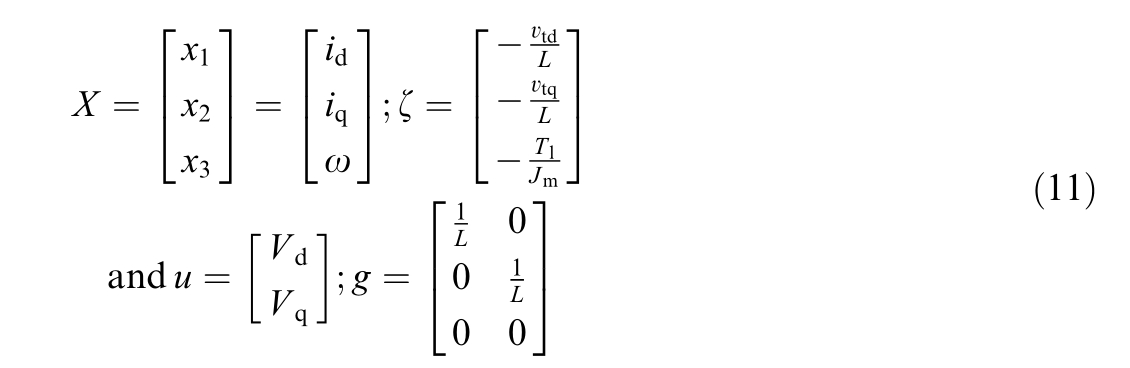
The energy function His defined as:

where the positive-definite diagonal matrix Q is defined as:

Then,can therefore be written as:

The gradient of the Hamiltonian function with respect to the state variables is given by:

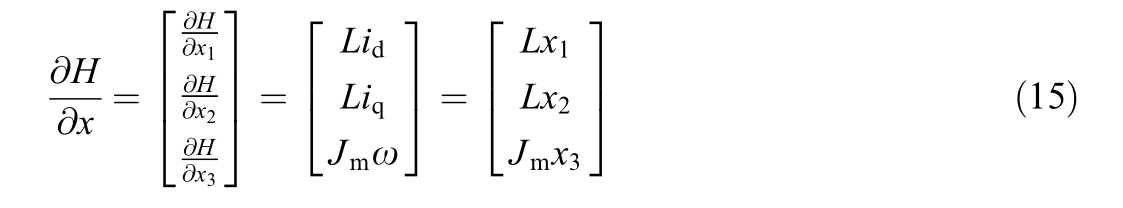
Consequently, the interconnection matrix J and the damping matrix R can be formulated as follows:

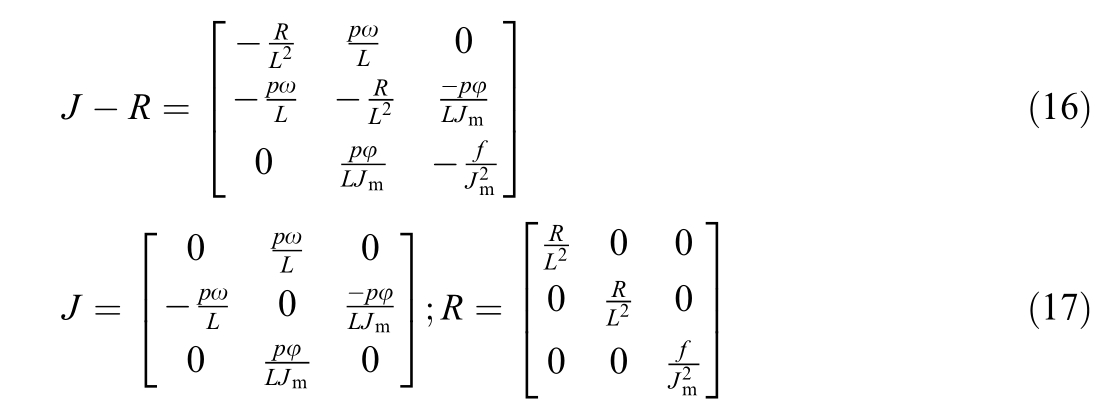
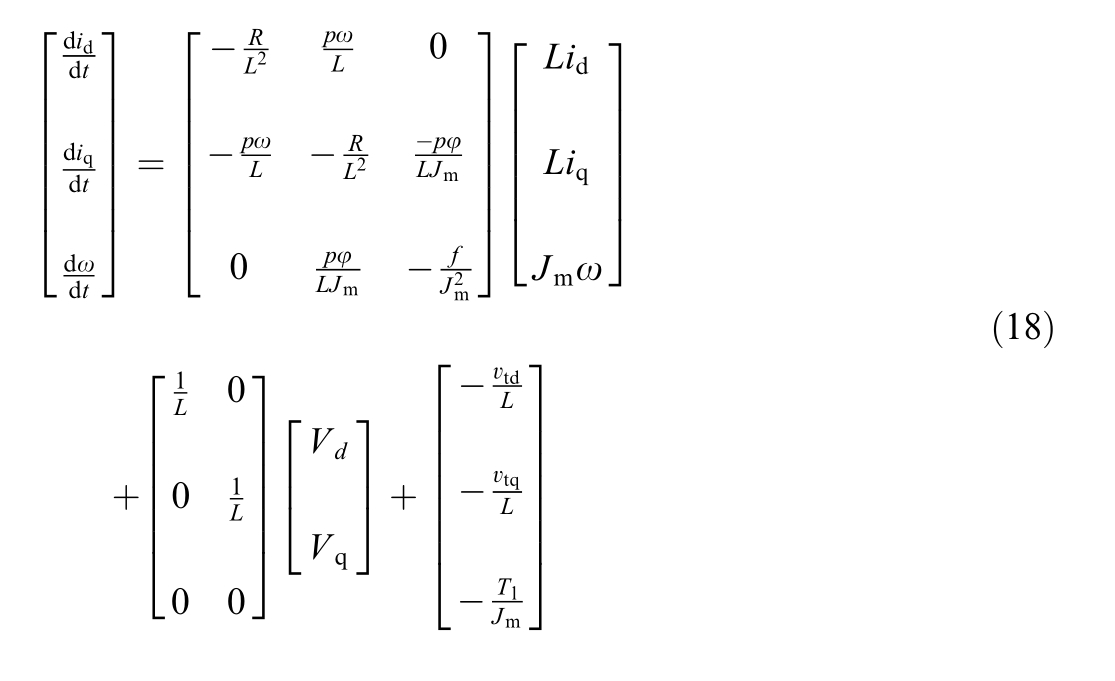
Finally, the complete state-space representation of the PMSM drive in Hamiltonian plant form is expressed as:

1.4 Proposed adaptive Hamiltonian control law

The intended set-point vector, Xref, is approached by the state vector, X.As a result,the tracking error state vector may be expressed as:

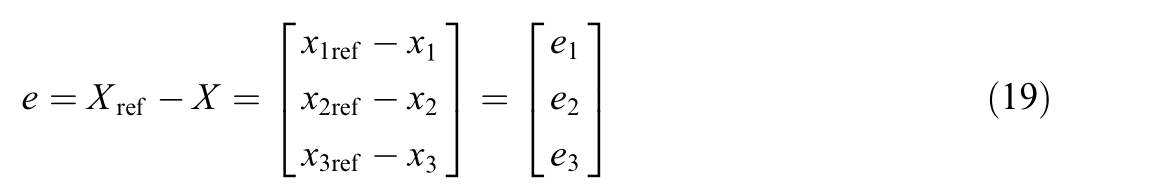
The desired Hamiltonian energy functi on is defined as:

Then, the gradient of Hdcan expressed as:

To definewe must start by defining the control matrices Jc and Rcsuch that:

Subsequently, we set J c and Rc to the same structure as J a n dR

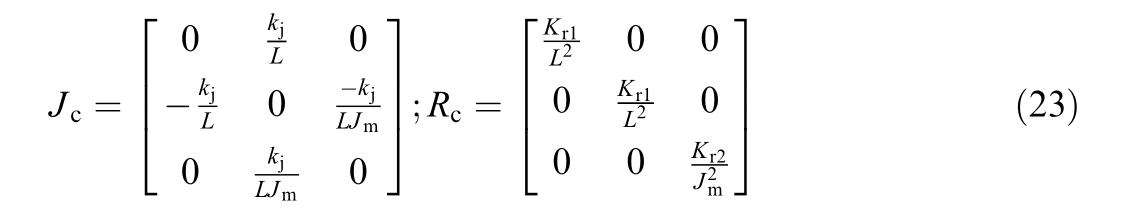
where Kr1 , Kr2 , and Kjare the damping controller gains.

Thus, Eq.(7) can be expressed as follows:

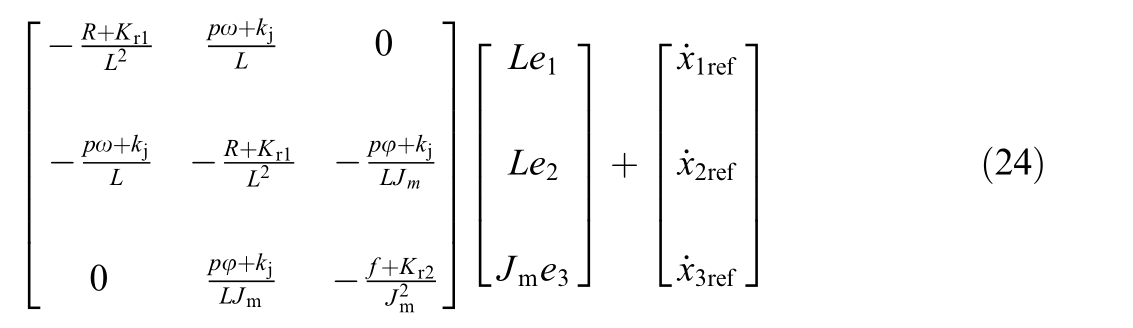
Finally, according t o (8), the control law can be solved and expressed as:

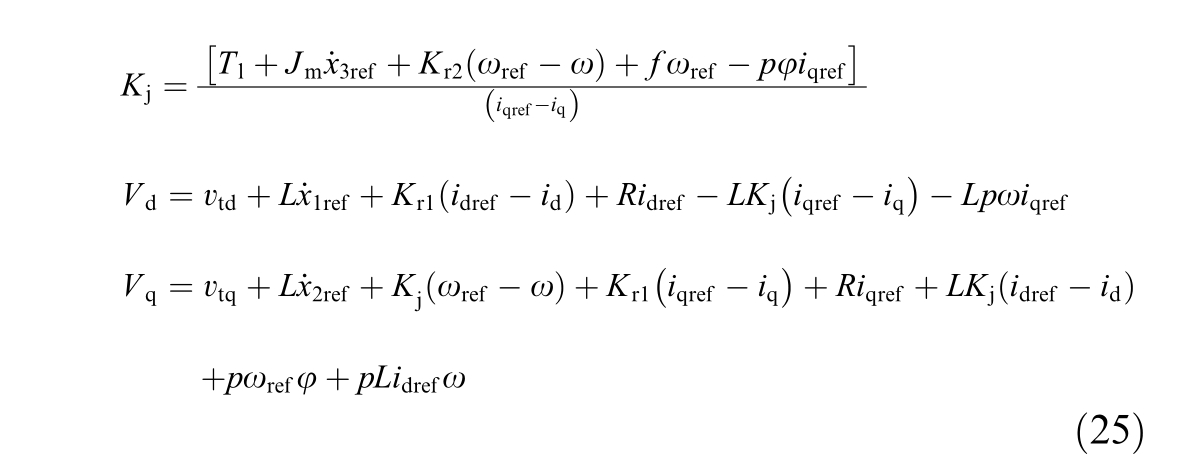
1.5 State-observer-based nonlinear parameters’ estimator

As previously discussed, the effectiveness of the Interconnection and Damping Assignment Passivity-Based Control (IDA-PBC) methodology relies heavily on the accuracy of the system model and its parameters.These parameters, including the internal losses within the Permanent Magnet Synchronous Motor(PMSM)and the associated Voltage Source Inverter (VSI), play a crucial role in shaping the closed-loop behavior [20].However, these losses are inherently time-varying and highly dependent on operating conditions, rendering the assumption of constant parameters inadequate for a broad range of realworld scenarios.

To account for these variations, the control design incorporates additional voltage drop terms, vtd and vtq,representing the aggregated internal losses of the PMSM and inverter.While these terms enhance model accuracy and mitigate control performance degradation due to unmodeled dynamics, they are themselves variable and must be estimated online to ensure consistent performance during both transient and steady-state operation.

Moreover, since the external load torque is typically unknown and subject to variation, its real-time estimation is equally essential for achievi ng robust control.To this end, a nonlinear disturbance observer is introduced in [21,22], compatible with the Port-Controlled Hamiltonian (PCH) structure underlying the IDA-PBC framework.This observer enables real-time estimation of both parametric losses and external disturbances,thereby enhancing control robustness and extending the operational reliability of the drive system across a wide range of conditions.

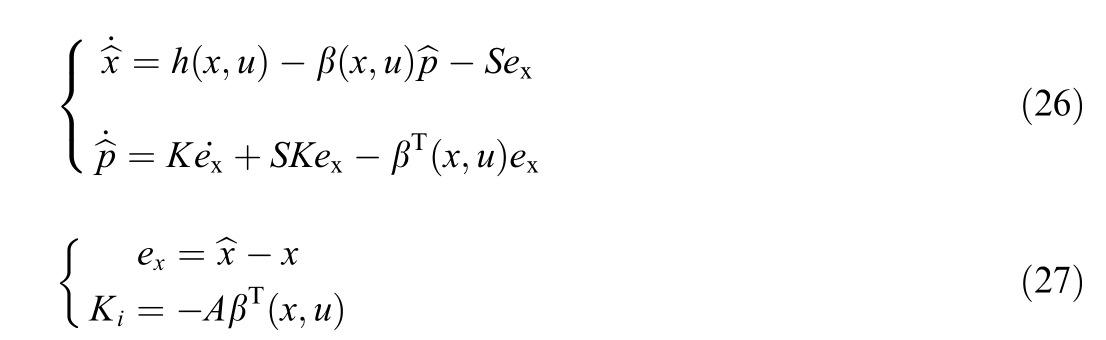
State-Observer for PMSM drive:

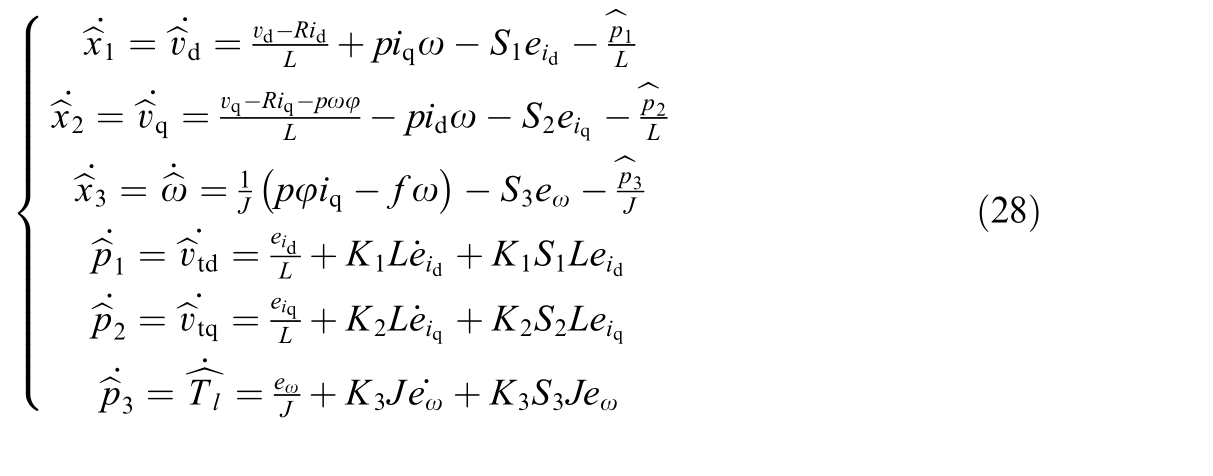
2 Speed controller and desired set-point generation

whereis the estimated torque using the observer.

The following equations provide feedback control principles that allow for an exponential tracking of the setpoints:

where Kpm , Kim are the controller parameters.

We can set the desired characteristic polynomial as follows:

where ξn1and ωn1are the desired damping ratio and natural frequency.

From (28) we can g et:

Eq.(27) became:

Finally, we must create a speed command for the inverter due to the nature of the derived feedback control law.We restrict the reference profiles to smooth the transitions between stationary regimes, since we are interested in a soft-start system.The motion trajectory planning is then described as:

where ξn2and ωn2are the desired damping ratio and natural frequency.

3 Control conclusion

3.1 Stability analysis

To assess the stability of the proposed closed-loop system, the desired Hamiltonian function is selected as a Lyapunov candidate:

The time derivative of this functi on is expressed as:

To further analyze the system properties, we leverage the characteristics of the control matrices.The matrix Jd is anti-symmetric, satisfyingwhich leads to:

Additionally, the damping matrix Rd is symmetric and positive definiteConsequently, the derivative ofsimplifies to:

From (35) and (38), it follows that:

According to Lyapunov’s stability theory, the function Hdis strictly decreasing over time.ensuring that the equilibrium point is globally asymptotically stable.This confirms the closed-loop stability of the system under the proposed IDA-PBC control strategy [7,8].

3.2 Control diagram

To ensure optimal speed control, the speed control loop must be designed with an appropriate cutoff frequency that adapts to the system dynamics.This cutofffrequency is selected to satisfy the condition:

where ωsrepresents the constant switching frequency of the power electronics.Furthermore, to achieve a critically damped system response and eliminate oscillatory behavior, the damping ratios are set to

The complete control scheme for the PMSM drive is illustrated in Fig.3.The current reference iqref is derived from the differential flatness control approach combined with inverse dynamics, as formulated in chapter 2.This reference signal is constrained within the allowable current range of the machine, defined by its rated limits:

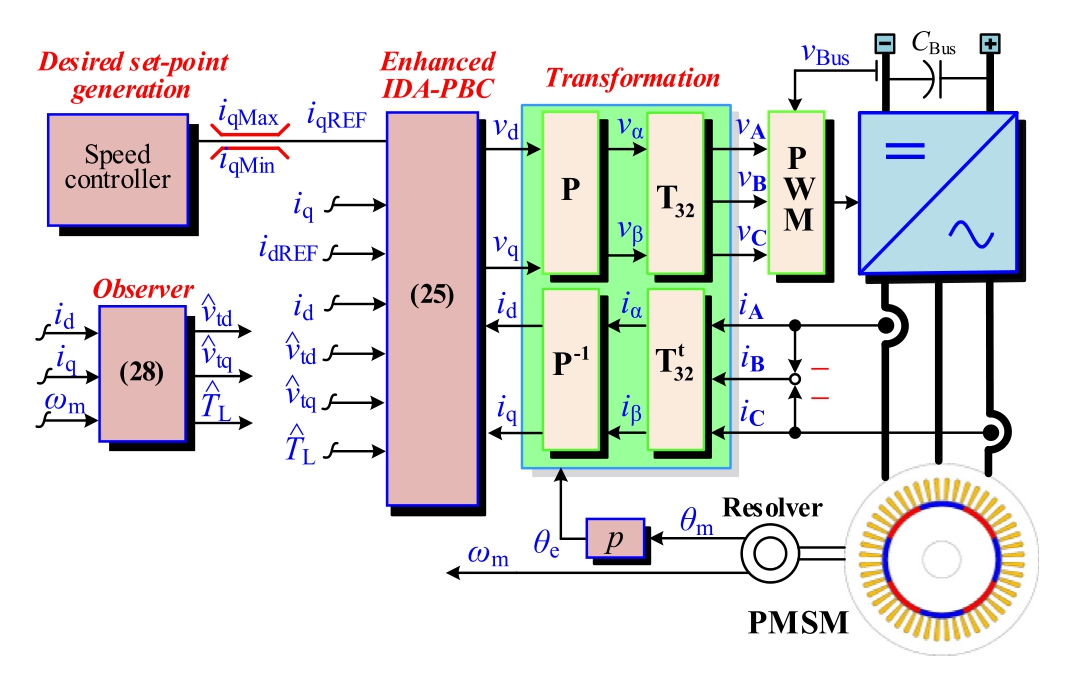
Fig.3.Proposed enhanced IDA-PBC with state-observers of a PMSM drive.

Subsequently, the enhanced IDA-PBC algorithm computes the corresponding voltage references v d an d v q ensuring precise tracking of the desired system response.

4 Control simulation

To evaluate the effectiveness of the proposed control strategies for the PMSM drive system, simulations were cond ucted using the Matlab/Simulink environment.Two distinct scenarios were examined:

4.1 Torque disturbance scenario

In the first scenario, a step change in the load torque from 0 to 3 (Nm) is applied at 0.5 s, while maintaining a constant speed at 2000 (rpm).This scenario is designed to assess the controller’s ability to reject disturbances and maintain precise speed regulation under sudden torque variation.

4.2 Speed reference variation

In the second scenario, a speed step change from 1500(rpm) to 3000 (rpm) is introduced at 0.5 s, while keeping the torque constant.

4.3 Results discussion

Fig.4 illustrates the applied load torque and its corresponding estimated value obtained through the proposed observer.The estimation closely follows the actual torque profile, demonstrating the accuracy and responsiveness of the observer in dynamic conditions.

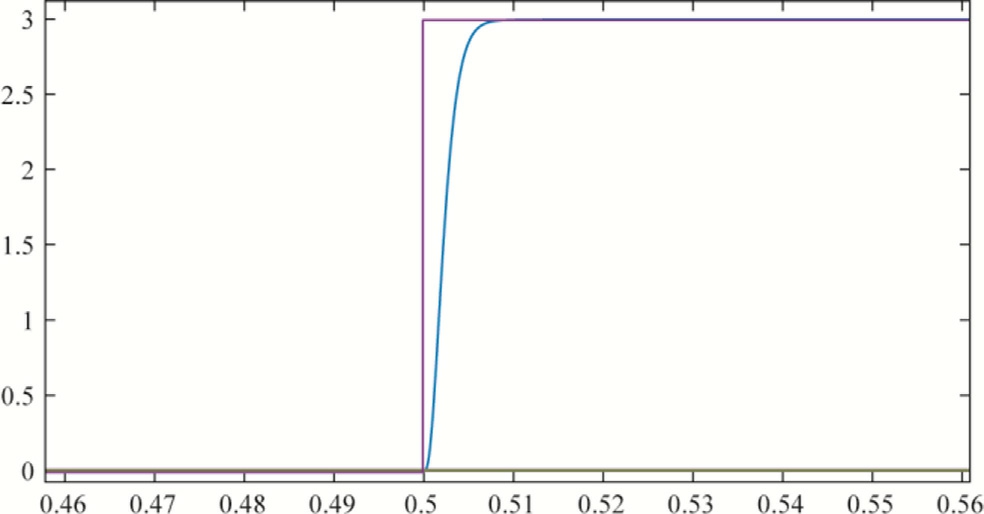
Fig.4.Load torque (N.m) reference (magenta) and estimated (blue)versus time under torque disturbance scenario.

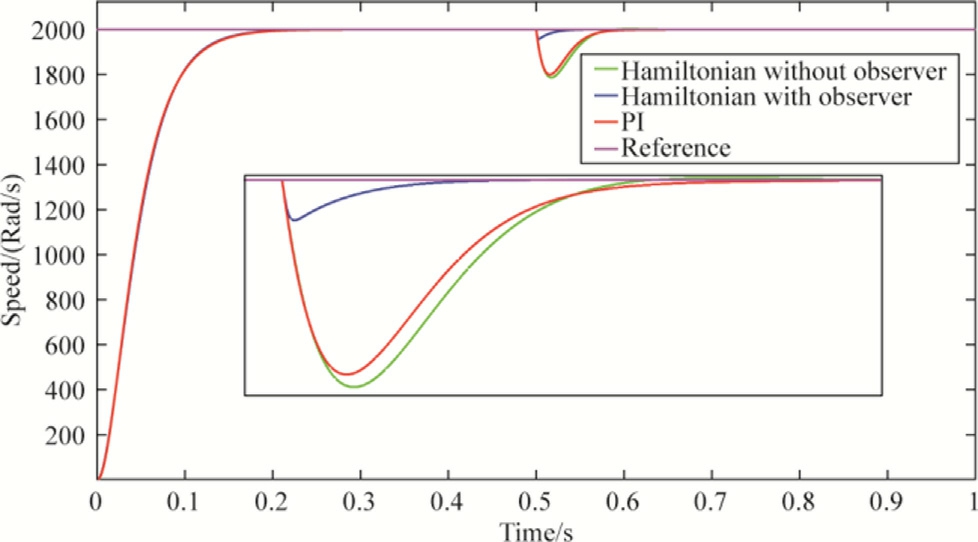
Fig.5.Speed (Rpm) versus time for different control strategies with a zoom on the speed transient, torque disturbance scenario.

Fig.5 presents the speed response under different control strategies following the application of a load torque disturbance.The Hamiltonian-based control without load torque estimation exhibits performance comparable to that of the conventional PI controller, both showing noticeable speed drops.In contrast, when the load torque estimator is integrated, the controller significantly mitigates the speed drop, achieving a faster recovery and better disturbance rejection.This improvement, however, is accompanied by a slight overshoot beyo nd the reference speed, which is characteristic of more aggressive compensation dynamics, as highlighted in Figs.6 and 7, which depict the corresponding electromagnetic torque and stator voltage responses.These responses clearly demonst rate a more assertive control behavior with faster reaction times.

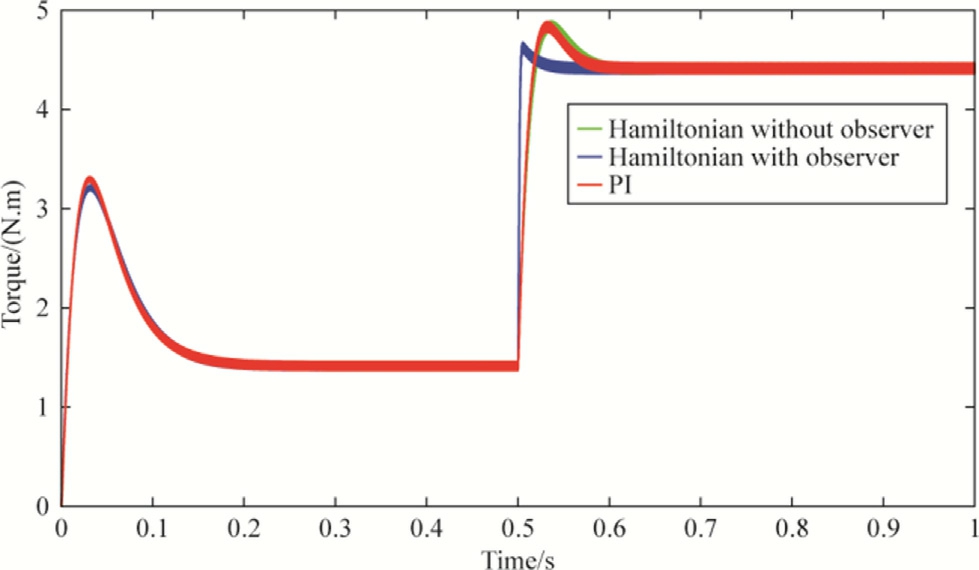
Fig.6.Torque (N.m) versus time for different control strategies, torque disturbance scenario.

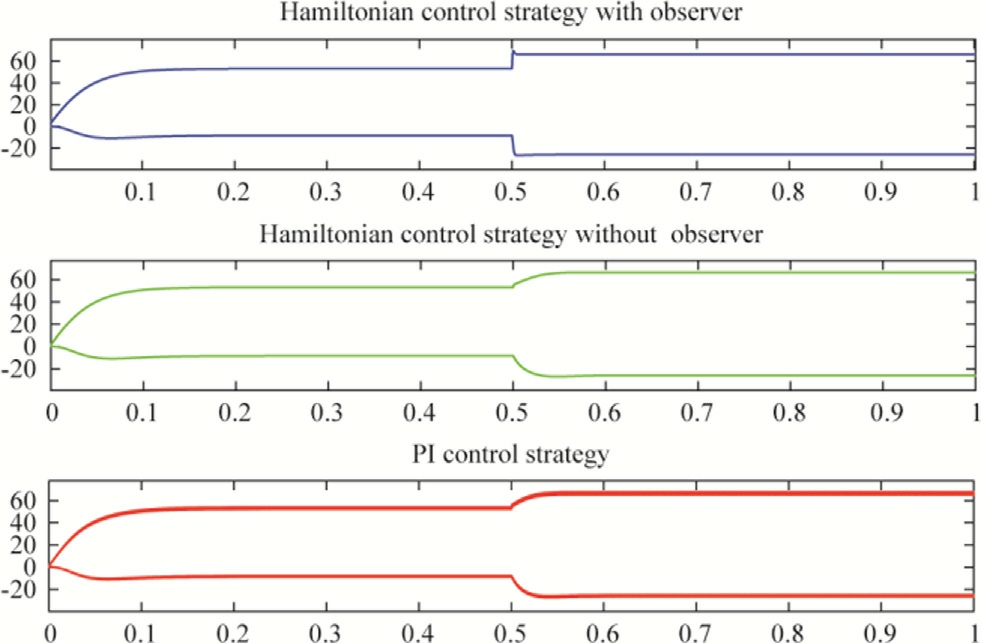
Fig.7.Direct and quadrature voltages (V) versus time, torque disturbance scenario.

In the case of a step cha nge in speed reference(Figs.8-10), performed without external torque disturbances, all three control strategies demonstrate comparable dynamic behavior.The speed tracking responses are well-aligned with the reference, showing minimal overshoot and fast settling times.This indicates that, under nominal conditions, the conventional PI controller and both Hamiltonian-based strategies provide satisfactory performance.

5 Experimental Validation

The experimental test bench used to validate the proposed control strategy (Fig.11) is built around a threephase permanent magnet synchronous motor (PMSM).The motor is supplied by a fully controlled three-phase voltage source inverter (VSI), which is managed in real time using a dSPACE MicroLabBox platform.This platform features a dual-core processor running at 2 GHz and supports a PWM switching frequency of 20 kHz.

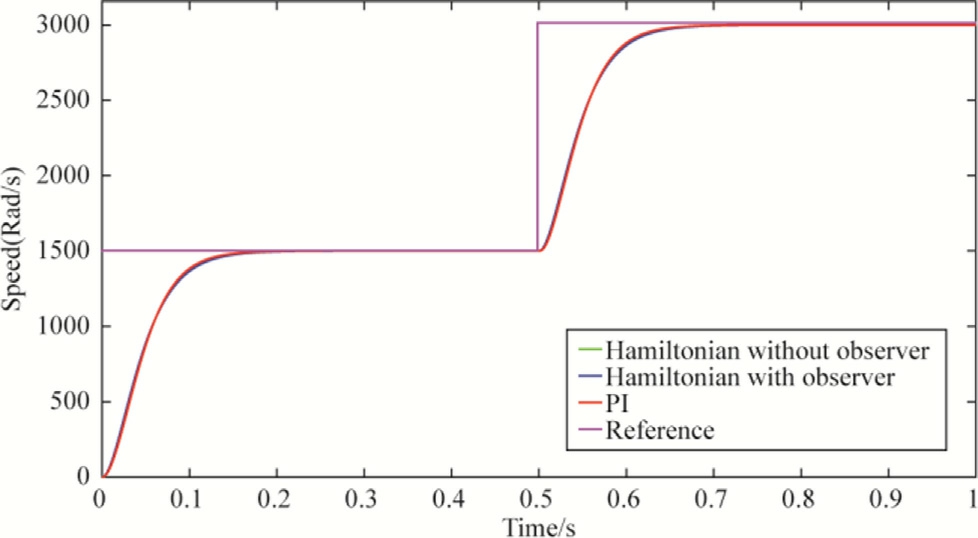
Fig.8.Speed (Rpm) versus time for different control strategies, speed reference variation scenario.

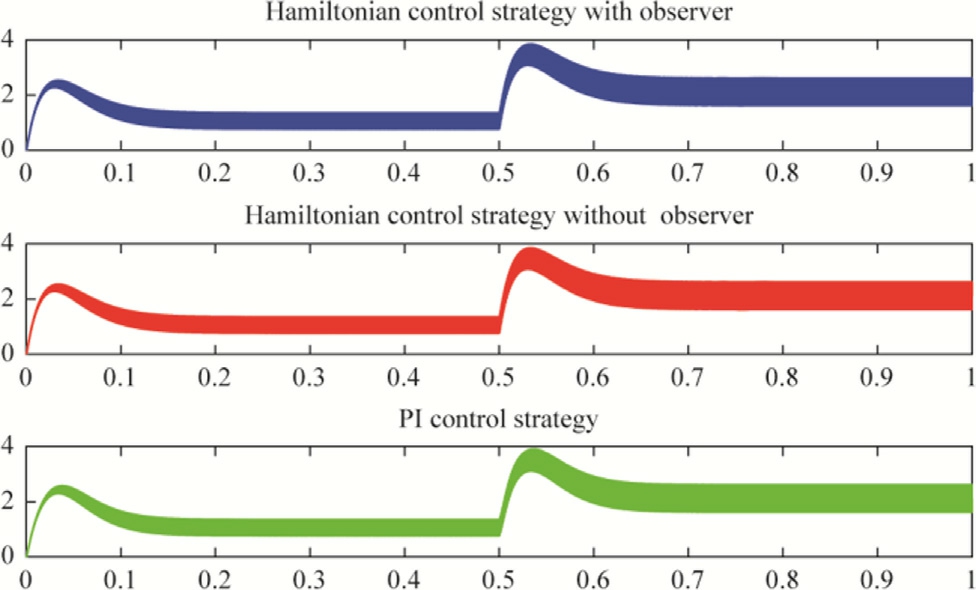
Fig.9.Torque (N.m) versus time, speed reference variation scenario.

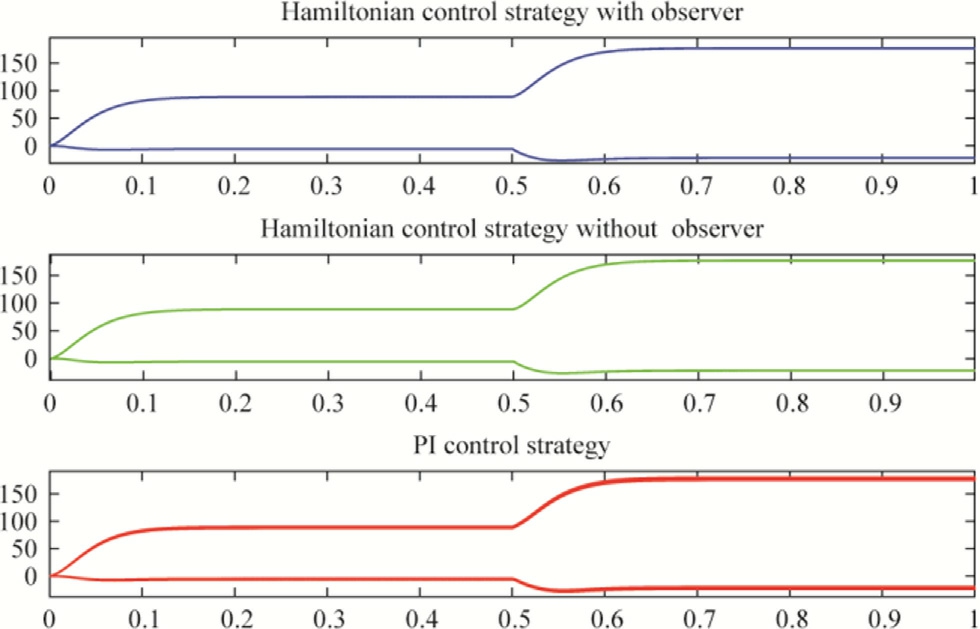
Fig.10.Direct and quadrature voltages (V) versus time, speed reference variation scenario.

The PMSM is mechanically coupled to a load machine,enabling accurate emulation of various load conditions.Additionally, a configurable resistive load is connected to the load machine via a circuit breaker, allowing load step changes to be applied during the tests.This setup enables the assessment of system performance under both steady-state and dynamic operating scenarios.

5.1 Parameter sensitivity analysis

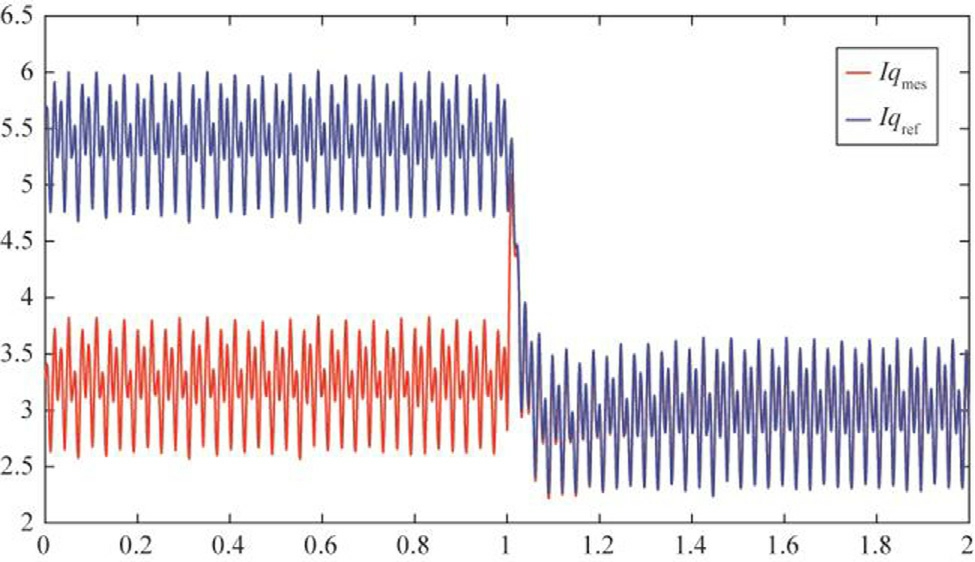
Fig.12.Current tracking performance under modeling uncertainties with observer activation at t = 1 s.

Fig.12 illustrates the transient behavior of the quadrature-axis current iq and its referen c eiqref during speed control operation under the proposed IDA-PBC framework enhanced with a nonlinear observer.To evaluate the robustness of the control strategy under realistic operating conditions, modeling uncertainties were introduced, including inverter dead-time effects, internal resistance variations of the motor.Initially, the control operates in open-loop simulation mode, where deviations between iq and iqref are noticeable, primarily due to the impact of these uncertainties.At t = 1 s, the nonlinear state and parameter observer is activated.The current immediately begins to track the reference more accurately,highlighting the observer’s role in compensating for parameter mismatches and disturbances.The results validate that the combination of IDA-PBC with an online observer not only ensures accurate reference tracking but also significantly enhances the system’s resilience to parameter variations and external disturbances, ensuring stable performance even under non-ideal conditions.

To evaluate the performance of the proposed control strategy, two distinct scenarios, aligned with those used during the simulation phase, were examined.In all cases,the voltage drop observer remained active.The control parameters used in the experiments are summarized in Table 1.

5.2 Speed reference variation

A step change in speed reference is introduced while maintaining constant load torque, to e valuate the dynamic tracking performance of the controller (Figs.13-15).

Fig.11.Test bench platform.

Table1 Control param eters.

Symbol Value Kr1 10 Kr2 0.01 ωn1 65 ωn2 40 Si 2500 Ki 200

5.3 Torque disturbance scenario

In the second experimental scenario, a step change in load torque is introduced at 0.4 s, while the rotor speed is maintained constant.This test is intended to evaluate the controller’s ability to reject disturbances and maintain precise speed regulation under sudden load variations.Moreover, it aims to assess the contribution of the load torque estimator to enhancing the overall performance and robustness of the control system in real-time operating conditions (Figs.16 -19).

5.4 Results discussion

Fig.16 illustrates the experimentally applied load torque alongside its corresponding estimated value, obtained using the proposed observer.The close tracking between the estimated and actual torque profiles confirms the observer’s accuracy and responsiveness under real-time operating conditions.

Fig.17 presents the experimental speed response under different control strategies following the application of a step change in load torque.Both the conventional PI controller and the Hamiltonian-based control without load torque estimation exhibit a noticeable speed drop.In contrast, the integration of the load torque observer significantly enhances disturbance rejection, effectively minimizing speed deviation and enabling a quicker return to the reference value.This improved performance is accompanied by a slight overshoot, indicative of a more assertive corrective action.Figs.18-19 illustrates the electromagnetic torque as well as the direct and quadrature voltages, highlighting a torque overshoot that contributes to rapidly restoring the desired speed.

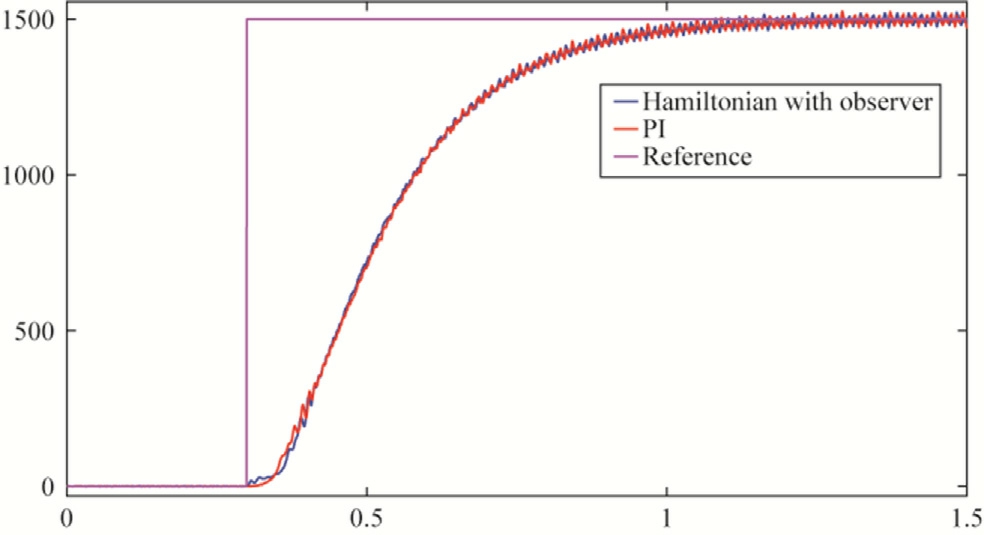
Fig.13.Speed (Rpm) versus time for different control strategies, speed reference variation scenario.

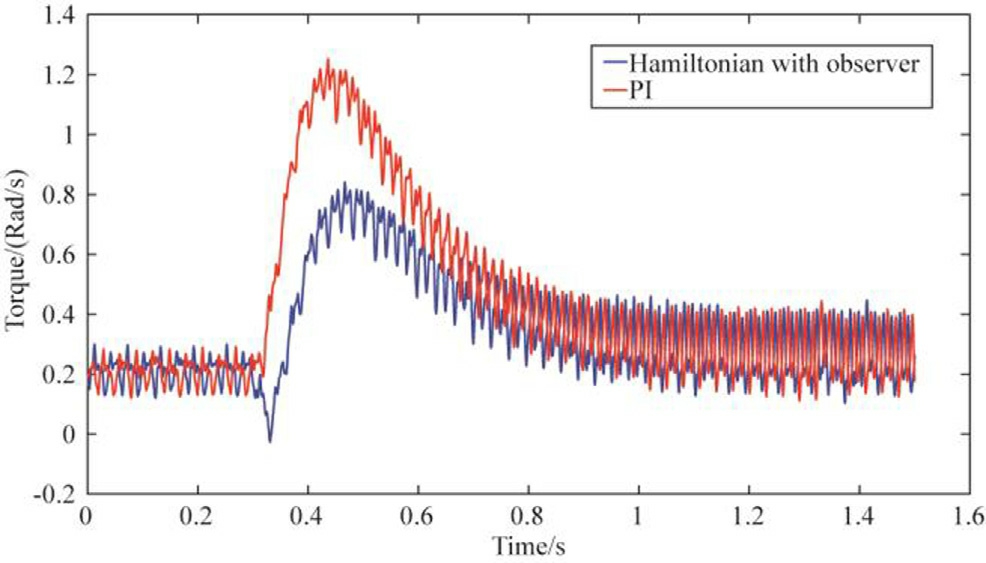
Fig.14.Torque (N.m) versus time, speed reference variation scenario.

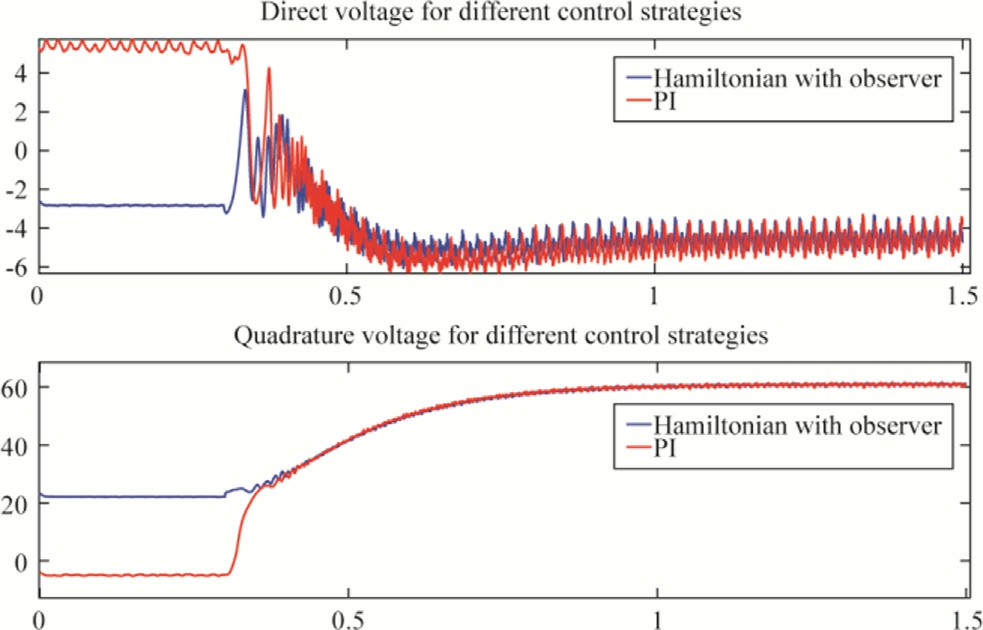
Fig.15.Direct and quadrature voltages (V) versus time, speed reference variation scenario.

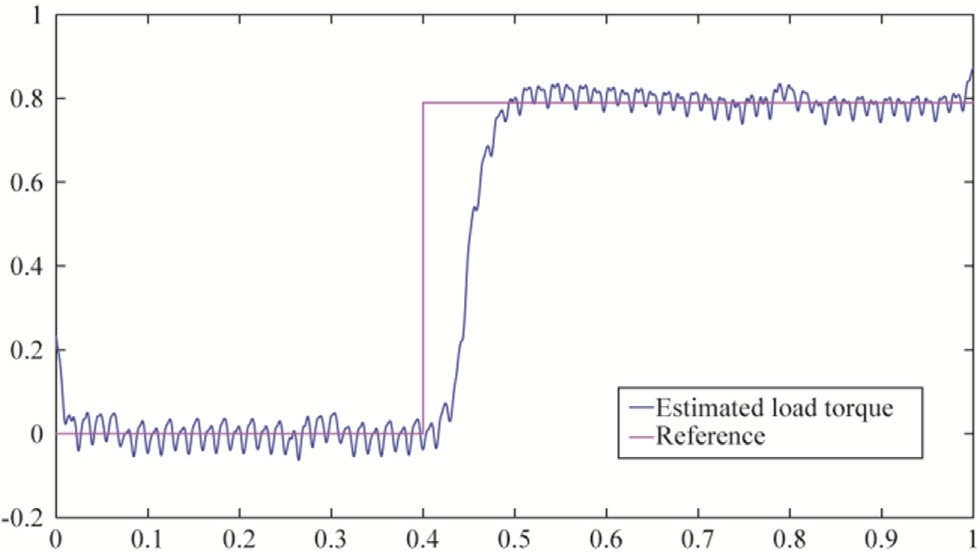
Fig.16.Load torque (N.m) reference (magenta) and estimated (blue)versus time under torque disturbance scenario.

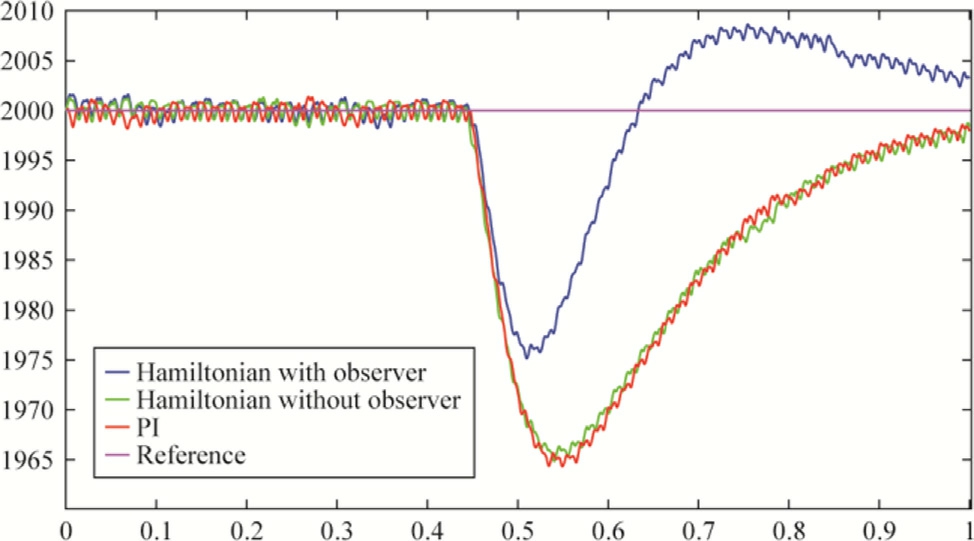
Fig.17.Speed (Rpm) versus time for different control strategies, a zoom on the speed transient, torque disturbance scenario.

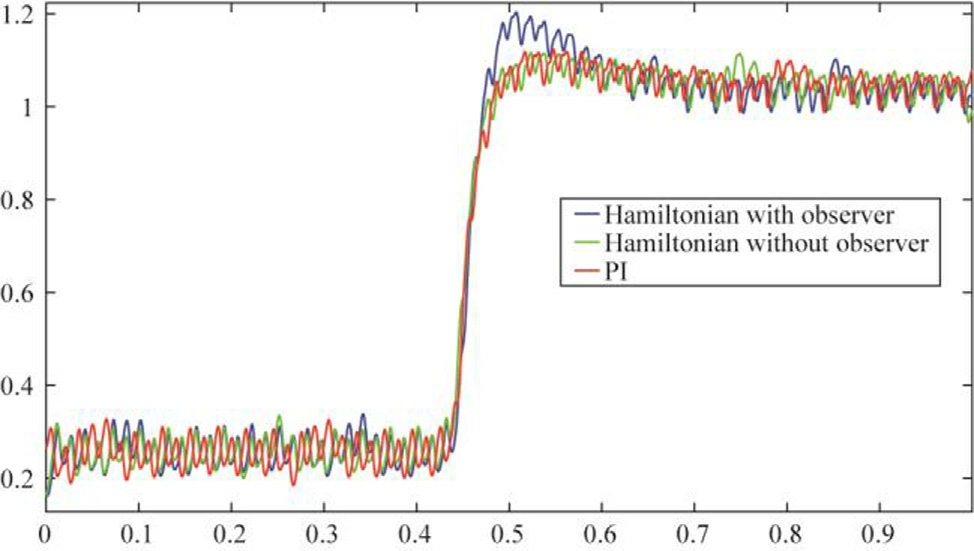
Fig.18.Torque (N.m) versus time, torque disturbance scenario.

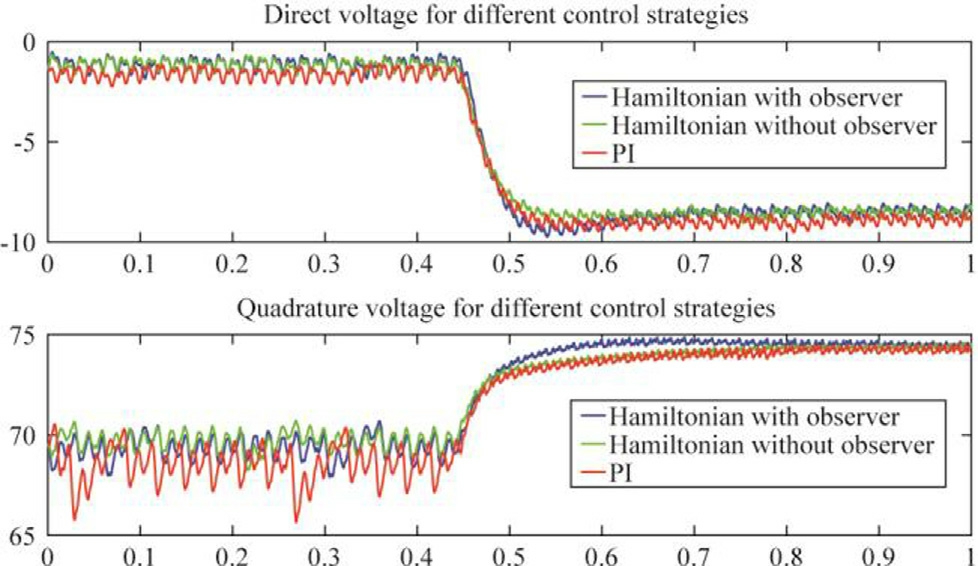
Fig.19.Direct and quadrature voltages (V) versus time, torque disturbance scenario.

In the scenario involving a step change in speed reference (in the absence of load disturbance), all two control strategies exhibit comparable dynamic performance, as shown in Fig.13.The experimental results confirm effective speed tracking with minimal overshoot and rapid settling time, indicating that under nominal conditions, the PI controller and the observer-enhanced Hamiltonian strategy all deliver satisfactory performance.Additionally,Fig.14 demonstrates that the Hamiltonian controller with observer achieves a smoother torque response with reduced overshoot and faster settling compared to the PI controller,further validating its superior dynamic response and robustness.

Using Control Desk’s execution time measurement capability, the computational times of both strategies,the Hamiltonian and the classical PI, were found to be similar.The increase in computation time due to online observer activation was minimal, rising from 6.2 to 6.7 microseconds.

6 Conclusion

This paper presented an enhanced Interconnection and Damping Assignment Passivity-Based Control strategy for PMSM drives.By integrating a nonlinear disturbance observer within the port-controlled Hamiltonian framework, the method effectively compensates for parameter uncertainties and external disturbances, enhancing system robustness.

The control scheme maintains the energy-based structure for systematic stability analysis and leverages trajectory derivatives to improve dynamic performance,including fast transients and accurate tracking.Despite these capabilities, it retains a simple architecture with few tunable parameters, facilitating real-time implementation.

Simulation and experimental results confirm the strategy’s effectiveness across various conditions, with performance comparisons against PI and standard IDA-PBC showing improved disturbance handling and tracking precision.While developed for non-salient pole machines,the approach is adaptable to other PMSM topologies through appropriate interconnection matrix selection, suggesting directions for future work.

CRediT authorship contribution statement

Mohamed Azzi: Writing - original draft, Conceptualization, Investigation, Validation, Software.Lotfi Baghli:Writing - review & editing, Conceptualization, Supervision, Software.Ehsan Jamshidpour: Conceptualization,Writing - review & editing, Supervision.Phatiphat Thounthong: Conceptualization, Funding acquisition, Writing -review & editing, Supervision. Noureddine Takorabet:Conceptualization, Funding acquisition, Writing - review& editing, Supervision.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported in part by an International Research Partnership ‘‘Electrical Engineering - Thai French Research Center (EE-TFRC)” under the project framework of the Lorraine Universite´ d’Excellence(LUE) in cooperation between Universite´ de Lorraine(France) and King Mongkut’s University of Technology North Bangkok (year 2021-2024/2025-28), in part by the National Research Council of Thailand (NRCT) under Research Team Promotion Grant (Senior Research Scholar Program) under Grant No.N42A 680561, and in part by the NSRF via the Program Management Unit for Human Resources&Institutional Development,Research and Innovation under Research project Grant No.B41G680025.